新型超高强Al-Zn-Mg-Cu铝合金热压缩变形的流变应力行为

臧金鑫, 郑林斌, 张坤, 陶乐晓

(1.北京航空材料研究院,北京 100095;2.成都飞机工业(集团)有限责任公司,成都 610092;3.太原科技大学,太原 030024)

Al-Zn-Mg-Cu系铝合金具有高比强度和良好的综合性能,是世界各国航空、航天及军事领域不可或缺的结构材料,通过高合金化、高纯化、精密热处理等方法,该系铝合金进一步向 600MPa级甚至700MPa级超高强度发展[1,2],并有望在飞机的主承力结构进一步扩大应用,更好地满足新一代先进武器装备的减重需求。

Al-Zn-Mg-Cu系铝合金要想获得良好的综合性能,必须经过挤压、轧制或锻造等高温塑性变形,而该系铝合金由于合金化程度较高,导致合金热加工性能降低,若变形温度及变形速率选择不当,在变形时很容易发生开裂[3]。近年来,国内外针对 7055, 7085,7050等高强Al-Zn-Mg-Cu合金的高温流变应力特征及材料本构方程进行了大量的研究[4～8],初步掌握了不同热变形条件下合金的流变应力值及热变形组织演变规律,建立了不同合金的高温变形本构方程,为合金后续热加工工艺的制定和实施提供了基础数据。本工作针对自行研制的新型超高强Al-7.5～8.7Zn-1.8～2.7Mg-1.4～2.1Cu合金,采用热力模拟试验方法研究了合金热压缩变形过程中流变应力行为,建立了材料热变形的本构方程,旨在为该合金合理制定热加工工艺参数提供理论依据。

1 实验材料与方法

实验材料为Al-7.5～8.7Zn-1.8～2.7Mg-1.4～2.1Cu合金铸锭,铸锭尺寸为(280mm,均匀化退火后在铸锭D/4直径位置处取φ8mm×12mm的圆柱体试样。在Gleeble-1500热模拟机上进行热压缩变形试验。变形温度分别为 300℃,350℃,380℃, 400℃,420℃,450℃,应变速率分别为 0.001s-1, 0.01s-1,0.1s-1,1s-1,总压缩变形量为 50%。为消除接触面上的摩擦,使压缩试样处于单向应力状态,实验过程中,试样两端垫有石墨纸。

2 实验结果与讨论

2.1 真应力-真应变曲线

Al-Zn-Mg-Cu合金在不同变形条件下热压缩变形的真应力-真应变曲线如图 1所示。

从图 1可以看出,在变形温度为 300～450℃和应变速率为0.001～1s-1的条件下,应力-应变曲线基本呈现稳态的动态回复型特征,即流变应力先随应变的增加迅速升高,当真应变达到一定值后,真应力并不随着应变的继续增大而发生明显的变化,呈现出较为明显的稳态流变特征。出现这种现象的原因是因为在热变形过程中,材料内部不断进行着两种相互竞争的过程,即加工硬化和加工软化过程。在变形初期,一方面材料内部位错密度增加,使材料硬化,一方面由于位错的重排和湮灭,使材料软化,但由于软化不足以补偿位错密度增加带来的硬化,因此,流变应力不断增加。随着变形量的增大,材料内部空位浓度也提高,位错的攀移在过渡变形阶段也开始产生作用,参与软化过程,从而使材料的软化程度提高,当位错增殖引起的应变硬化与位错交滑移、攀移以及位错的脱钉等引起的软化达到动态平衡时,真应力基本保持恒定,即变形进入稳态流变阶段。

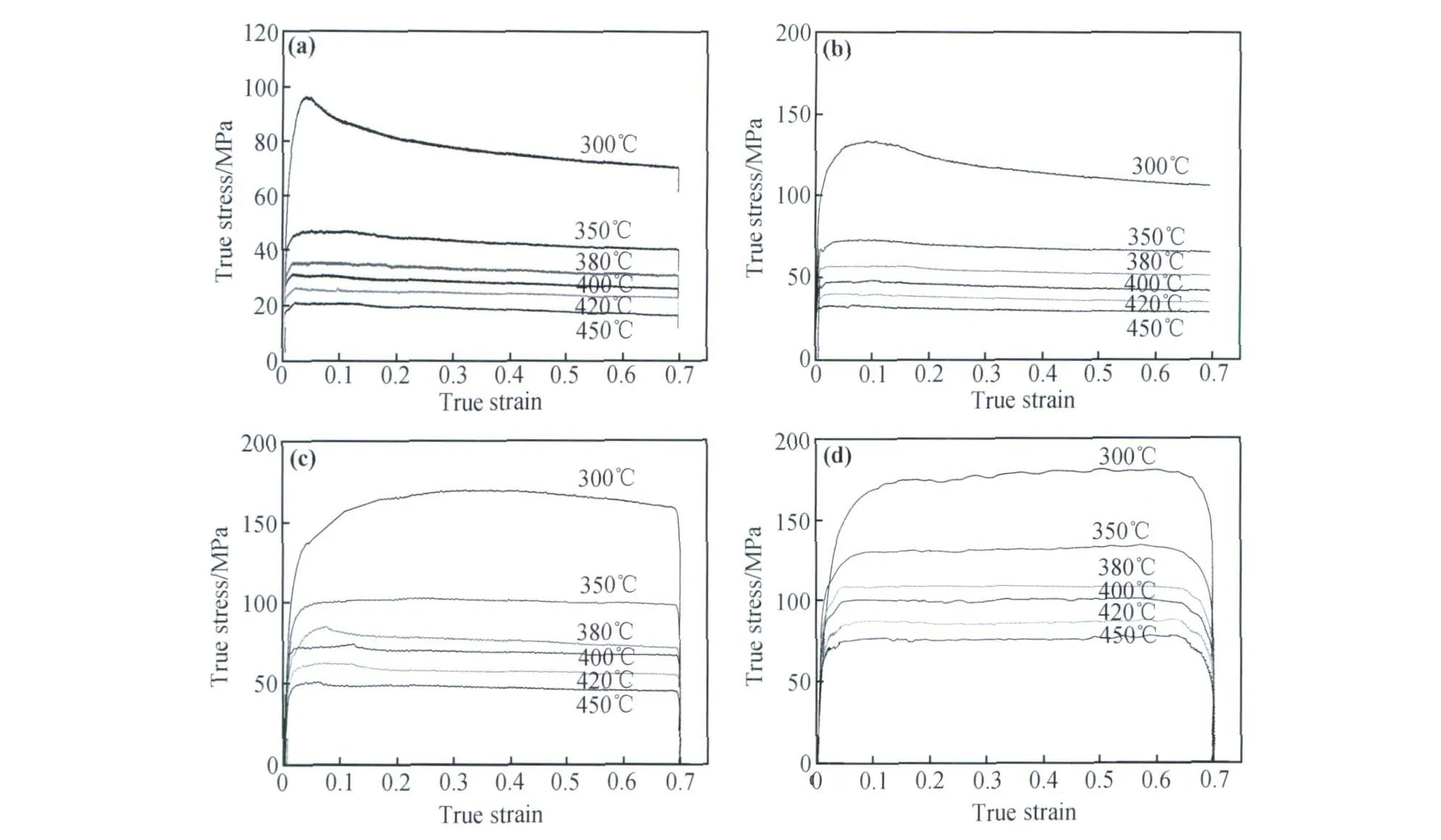
图1 Al-Zn-Mg-Cu合金热压缩变形的真应力-真应变曲线Fig.1 True stress-strain curves of Al-Zn-Mg-Cu alloy at different temperatures and strain rates (a)ε﹒=0.001s-1;(b)ε﹒=0.01s-1;(c)ε﹒=0.1s-1;(d)ε﹒=1s-1

从图 1还可以看出,在相同的应变速率条件下,合金流变应力随变形温度的升高而显著降低。在相同的变形温度下,合金的流变应力随应变速率增加而升高。这是因为：当应变速率恒定时,随着变形温度升高,基体中原子活动能力增强,原子间的结合力降低,合金变形时临界切应力降低,更多的滑移系得以启动;而且位错攀移能力增强,位错间相互湮灭更加明显,软化程度增大,从而导致合金的应力水平降低。当变形温度不变时,一方面,随着应变速率增大,在同一应变量下产生的位错增多,位错运动速度增大,位错间相互交割的几率增多,因而提高了变形时的临界切应力;另一方面,应变速率升高时,单位应变的变形时间缩短,位错被激活的时间缩短,使得动态回复或动态再结晶等流变应力软化行为不能充分进行。

2.2 流变应力方程的建立

研究表明[9,10],金属和合金的热加工变形和高温蠕变一样都存在热激活过程,应变速率受热激活过程控制。虽然热加工变形时的应变速率通常比蠕变时的应变速率大几个数量级,但热加工仍可视为蠕变在大应变速率和较高的应力水平下的一种外延,两者的变形机制和软化机制都非常相似。为此, Sellars和Tegart于1966年提出了一种包括变形激活能Q和温度的双曲正弦形式的修正Arrhenius关系[11]来描述这种热激活稳定变形行为：

其中：

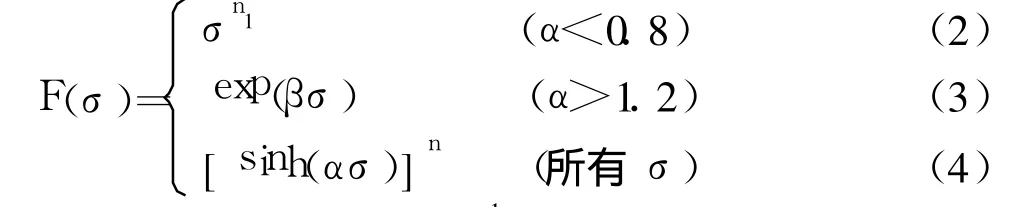
式中：ε﹒为应变速率(s-1);R为气体常数(8.31J/ mol(K));T为绝对温度(K);Q为变形激活能(kJ/ mol);σ为流变应力(MPa);A,α,n和n1为材料常数,其中α=β/n1。A为结构因子(s-1),α为应力水平参数(MPa-1),n为应力指数。

温度和变形速率对材料变形行为的影响还可以用温度补偿的应变速率因子Zener-Hollomon参数(简称Z参数)来描述：

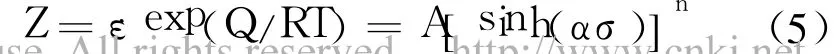
Arrhenius方程的双曲正弦函数形式较好地考虑了热变形条件(T,ε﹒)的综合作用。这里取σ为稳态应力。

将式(2),(3)带入式(1)并两边取对数得：

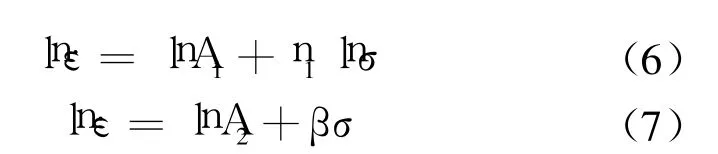
在同一温度条件下,式中lnA都为常数。分别做lnε﹒-lnσ,lnε﹒-σ关系图。如图2所示。

图2 稳态应力与应变速率的关系Fig.2 Relationship between stresses and strain rates (a)lnε﹒-σ;(b)lnε﹒-lnσ

由式(6)(7)可知,当温度一定时,n1和β分别为lnε﹒-lnσ和lnε﹒-σ曲线的斜率。采用线性回归处理,如图2所示,相关系数均大于 0.99。n1值取图2 (a)中稳态应力较低,即温度为 380～450℃的直线斜率的平均值,得到n1=5.35532。β取图2(b)中稳态应力较高,即温度为 300～350℃的 2条直线斜率的平均值,得到 β=0.0689。则 α=β/n1= 0.01287MPa-1。

假定热变形激活能Q与温度T无关,对式(1)两边分别取对数,整理得：

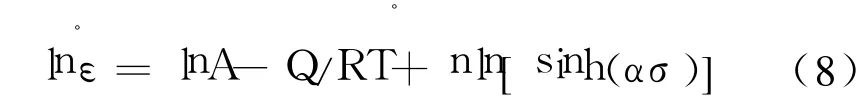
在一定温度下,对式(8)两边取对数得：

在一定应变速率下,对式(8)两边取对数得：

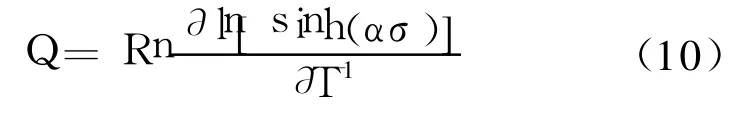
将图1中不同温度下Al-Zn-Mg-Cu铝合金变形时的稳态应力、应变速率值和 α值分别带入式(8),再用最小二乘法线性回归处理,分别绘制相应的 ln关系曲线(图3)和ln[sinh(ασ)]-1/T关系曲线(图4),直线的斜率分别为应力指数n和Q/nR。

由图3,4可以得出,变形激活能Q=169.92kJ/ mol,应力指数n=4.5537。

对式(5)两边取对数可以得到：

图5所示为lnZ-ln[sinh(ασ)]关系曲线。采用一元线性回归分析可以得出两者的关系为lnZ= 28.029+0.987nln[sinh(ασ)],相关系数达到0.99以上。由此可以得出材料常数 A为1.49×1012s-1。

图5 稳态应力与Z参数的关系Fig.5 Relationship between flow stresses and Z parameters

由上述可以得到适用于该合金所有应力状态的稳态流变应力本构方程：

变形激活能反映了合金热变形的难易程度,表1给出了相关文献中 7000系铝合金及纯铝的变形激活能。从表 1的数据可以看出,7000系铝合金的变形激活能比多晶纯铝的高,这是因为Zn,Mg,Cu等合金元素的加入,形成了第二相粒子,这些第二相粒子在金属塑性变形的过程中,会阻碍位错的运动,使位错交滑移和攀移所需要的能量增加,从而提高了变形激活能。

表1 7000系铝合金的变形激活能Tab le 1 Activation energy of the 7000 series alloys

与 7050,7085等 7000系高强合金相比,新型合金的热变形激活能与 7050相当,比 7085的稍低,表明新型合金的热变形难易程度与 7050相当,比7085更易热变形。该新型合金的合金元素含量比7050及 7085的都要高,但热变形激活能与二者相当或略低,表明该合金有很好的热加工性能。这一方面是因为该合金铸锭的均匀化程度较高,除少数非平衡相在晶界析出外,大部分以平衡析出相的形式存在,在热变形过程中,大部分平衡析出相发生了回溶,阻碍位错运动的第二相粒子大量减少,导致热变形激活能较低;另一方面是因为合金元素的加入会造成合金在塑性变形过程中形成的亚结构更加密集,大量的亚晶界与基体间存在的原子错配使合金在塑性变形过程中产生更多的空位,会促进位错的重排和湮灭,增大了合金的回复驱动力,导致合金的变形激活能降低。

3 结论

(1)新型Al-7.5～8.7Zn-1.8～2.7Mg-1.4～2.1Cu-0.11Zr铝合金为应变速率敏感材料,应变速率和变形温度对合金的流变应力有显著影响,热变形流变应力随温度升高而降低,随应变速率的增加而增大。

(2)新型Al-7.5～8.7Zn-1.8～2.7Mg-1.4～2.1Cu-0.11Zr铝合金可以用包含Arrhenius项的本构过程描述其稳态变形时的流变应力行为。流变应力本构方程可以表示为：ε﹒=1.49× 1012[sinh(0.01287σ)]4.5537×exp(-1.6992× 105/RT)。

[1]王洪,付高峰,孙继红,等.超高强铝合金研究进展 [J].材料导报,2006,20(2)：58～60.

[2]CASSADAW,LIU J,STALEY J.Aluminum alloys for aircraftstructures[J].AdvMater Proc,2002,160(12)：27.

[3]POIRIER JP.晶体的高温塑性变形[M].关德林,译.大连：大连理工大学出版社,1989.

[5]李俊鹏,沈健,许小静,等,7050高强铝合金高温塑性变形的流变应力研究[J].稀有金属,2009,33(3)：318～322.

[6]PUCHIE S,STAIA M H.High-temperature deformation of commercial-purity aluminum[J].MetallMater Trans(A), 1998,29(9)：2345.

[7]王亮,李惠曲,陈慧琴,等.Al-Zn-Mg-Cu合金热压缩流变应力行为及组织演变[J].锻压技术,2010,(35)4：133～136.

[8]SERAJZADEH S.Modeling flow stress behavior of alum inum alloys during hot rolling[J].Materials Science and Technology,2006,22(6)：713-718.

[9]李杰,尹志民,黄继武,等.超高强Al-Zn-Mg-Cu-Zr合金的热变形行为[J].稀有金属,2004,28(1)：166-170.

[10]DAVENPOTS B,SILK N J,SPARKSCN,etal.Development of constitutive equations for modeling of hot rolling.[J].Mater Sci Technol,2000,16(5)：539-542.

[11]SHEPPARD T,JACKSON A.Constitutive equations for use in prediction of flow stress during extrusion of aluminum alloys[J].Mater SciTechnol,1997,13(3)：203-206.

[12]SELLARS C M,On the mechanism of hot deformation [J].Acta Met,1966,14：1136-1138.