等高线放样建模在水电站虚拟现实系统中的应用

孙浩鹏

（长春工程学院科学技术处，长春 130012）

0 引言

本次建模的目的是应用于基于虚拟现实的水轮机运行控制仿真，在项目初始阶段的建模过程中选择了省内某水电站，并得到此水电站周围山脉的等高线图。目前较常用的三维地图的建模方法，是从等高线地形图中取得离散点高程数据，然后利用Delaunay三角网［1］对离散高程数据点进行三维建模，经过试验发现其缺点是模型数据量巨大，多边形模型的三角化在UV展开时困难等，导致虚拟现实的应用不能完全满足要求。故提出新的建模方法，利用NURBS（非标准样条曲线）方法中的LOFT（放样建模）建成NURBS模型，之后将所得的NURBS模型转换成四边形的多边形模型。分析步骤及算法实现，并给出所生成的三维地形图实例，其构建的三维地形符合等高线的规律，构建的模型运行速度快，生成的立体图像逼真，在虚拟现实系统中运行良好。

1 放样建模对等高线的需求分析

模型的建立在三维软件中选择LOFT方式，此命令是通过多个曲线之间的点连成面的建模方式，它要求所提供的截面形状曲线必须是一个封闭的曲线，在得到形状曲线上所有顶点数据以后，必须重新参数化这条曲线，并以用户所给出的曲线上的顶点顺序来存储这些顶点数据，得到的等高线同一地点的每个曲线上的点个数最好相同。普通等高线的绘制在某个山体的山顶处如果忽略，在建模时，要根据山体的走向来估算山顶的高度并自动建立一个放缩比为零的点个数相同的曲线以作为建模中山顶的封闭线体。对于大型山脉的多个山体交汇处等高线称之为鞍部，这里的表现为不同的多个同心圆相邻，鞍部的建模需要将包围相邻同心圆的大圆在相邻同心圆中心处断开，成为两个独立的圆并分别放样。

2 常用算法分析

目前常用方法为通过读取等高线离散数据点来构建三角网，根据Delaunay三角网构建过程的不同，一般把生成Delaunay三角网的算法分为插入法、生长法和分治法［2］。逐点插入法于1977年由Lawson提出［3］，随后有众多学者对其进行了改进。此方法思路基本如下：先通过离散点构建初始大三角形，并随机排列点集P中的所有点P0，P1，…。如果点集P中的点Pa被三角形PiPjPk包含，就连接点Pa和三角形PiPjPk的各个顶点，将其划分成3个三角形；如果Pa在三角形PiPjPk的边PiPj上，则连接Pa与共边PiPj的2个三角形的第3个点，剖分形成4个子三角形，以此类推。在最后通过边交换方法规格化三角剖分并移除包含大三角形任意顶点的所有三角形，当在三角网中新插入一个点P后，三角网通过边交换等方法进行重构优化。由于生长方法消耗的时间过长，所以近年来已经很少用到此方法。分治算法思想［4］于1975年由Shamos和Hoey提出，并由多位科学家对其进行了改进。其主要原理是根据点坐标对点集进行排序后将点集二分成2个点集Va，Vb；当两个点集中的数量超过3则再次分成2个下层点集，当所有点集分解成小于3的点集后，合并Va，Vb。其思路是将点集分割成易于生成三角网的数据点集合，然后把子集中的能构成三角网的点合并，经优化生成最终的三角网。通过比较看出，插入法对计算机的硬件要求较低，但是时间较长，分治法对计算机硬件要求较高，时间上比插入法优秀。通过对常用算法的分析得知，在形成山体的过程中三角面个数过多，为了减少数量而优化又导致三角网分布明显混乱，对后期的UV分解造成明显的困难和干扰。

3 扫描得到等高线及点自动运算

Leberl在1982年通过对等高线、水系、山脊线的矢量化进行了自动提取［5］。Greenlee是较早尝试扫描法对等高线的提取的［6］。大体步骤先将纸质地形图扫描为数字栅格地形图，通过滤波去噪得到彩色分割得到二值化等高线图，细化二值等高线图并处理等高线粘连处理和断线的连接。在得到完整的等高线图后，操作过程如下：首先通过直接读取等高线到三维软件中，并建立每条线的变量数据格式库，每条线的高度值也读入并依据高度将各条曲线空间上沿着Y轴移动至相应高度点，结果如图1所示。在读入线后我们需要使每条线上的曲线点尽量减少，在LOFT放样建模中，一般的环形闭合曲线需要8个点就可以了。通过程序对每条线自动进行重新构建，即在读入的曲线上按照等间距读取8个点，并依据这8个点构建新的曲线如图2所示。这样在三维软件中的曲线就可以达到最优化的建模方式了。

图1 等高线高度定位

图2 等高线优化点

实现程序伪代码如下：

｛

Int ID，KK；//定义线条数的ID和重构曲线点参数

Float high［］；//读取每条线的高度值

For（line＝0；line＋＋；）

｛

Select－r curve（ID）；

set Attr"curve（ID）.translateY"high［ID＋

1］；//根据每条线的高度值将线移动

select－r curve（ID）；

rebuild Curve－ch 1－rpo 1－rt 0－end 1－kr 0－kcp 0－kep 1－kt 0－s KK－d 3－tol 0.01"curve（line）"；//对曲线根据所给的变量KK进行点重构

select–cl；

｝｝

4 分段添加等高线的实现

在得到的等高线图中有非同心圆类等高线时，需要对线体进行判断。判断此线是否包含2个或者2个以上同心圆类的等高线。判断算法利用每条线体的重心值的偏差，如果是同一个山脊，等高线的重心值在Y轴上依次升高的同时在X和Z轴上的偏差是比较小的。如果是不同的2个山脊，在等高线读取过程中就会得知线体的重心在X轴和Z轴上会有较大的突变型偏差，最外围的等高线的重心与任意包含于它的等高线重心偏差都会大于同一个山脊的等高线重心偏差值。这样我们就利用2个差量即重心的X和Z的差量判断出等高线是否来自同一个山脊。当差量大于我们给定的恒量时，我们需要对变化的等高线进行分析，如果任意等高线内包含的山脊数为1，则不进行分段处理。如果任意等高线内包含的山脊数大于2，则将等高线重心差量过大的那根线自动切割成内包含山脊个数一样的闭合线。分割曲线由所包含的山脊的中心决定，在各山脊的中心点连线，先算出连线的中心点设定为C点，并计算所连线与所需分割曲线的断点K1和K2，断点的选择由经过C点的直线与所需分割线相交得到。此时将2个分割的交点K1、K2和C点共3个点连成一条直线L，这样就可以用L复制后和分割的曲线连成两个闭合的曲线。

当待分割等高线内包含3个或3个以上山脊时，如图4所示，先分别计算出各组山脊的重心，将彼此连接后得到的线体看为一个三角形，分别求得各条边的中点C1、C2和C3，直接做各边的垂线与外围等高线相交处记为K1、K2、和K3，虽然有细微偏差，在运算过程中为了提高速度忽略交线的夹角。当包含山脊个数大于3时，可以直接以各个山脊单独建模，到最后用焊接的方法得到山脊底部统一的模型。程序流程如图3所示。

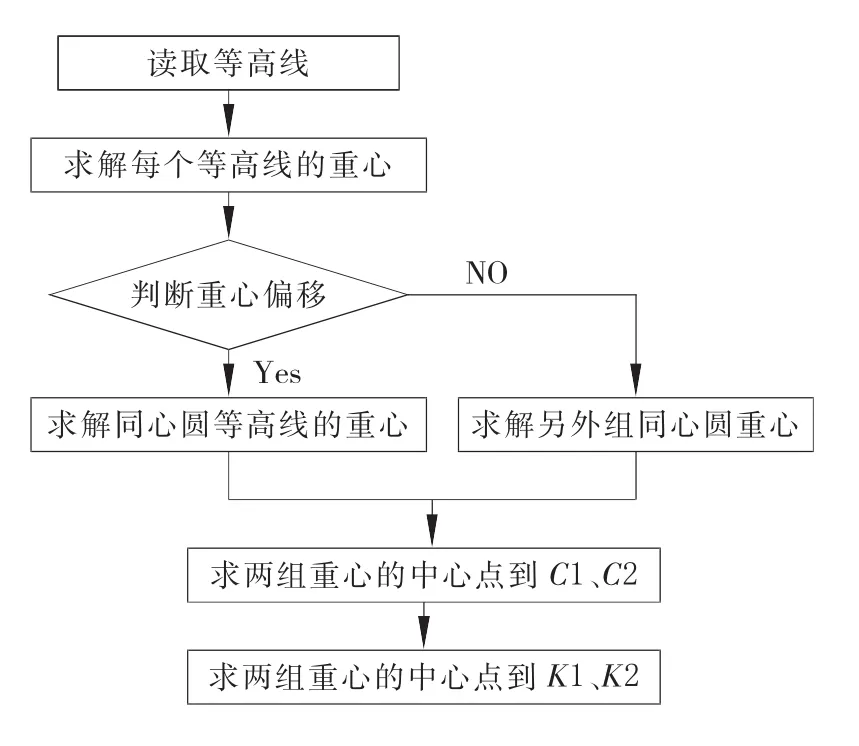
图3 程序流程图

图4 多山脊等高线添加点示意图

根据流程图得到的求解C点和K点的伪代码如下：

｛

float＊Pivots＝new float［sizev＊sizeu＊3］；//定义重心、线

Pivots［i］［j］［k］//定义三维数组重心

For（Int i＝1；i＋＋；i＜ID）//此处ID为等高线的总数量

Pivot［i］［j］［k］＝getattrib pivot Line［i］；

If Pivot［i］［j］［k］－ Pivot［i＋1］［j＋1］［k＋1］＞Q//Q为指定恒量

Mark Line［i］；//将当前的等高线编号记录下来作为将要分段的线

soGeo Line.AddPart（part As soPoints）//利用两组重心点平均值建立线

if（abs（x1－x0）＞＝abs（y1－y0））

｛Length＝abs（x1－x0）EPCurveTool；

curve－d 3－p k1－p k2－p k3；//通过K1，K2，K3得到新的直线

select－tgl nurbsCircle1；

intersectCrvPreset 1 0.01 2 0 1 0 1；//计算后得到新的交点

select－r Line.u［i］；

detachCurve－ch 1－cos on－rpo 1 Line.u［i］.Line.u［i＋1］；//分离Line［i］

｝

这样就通过首先求解相交曲线点，从当前点断开曲线得到新的闭合曲线，从而达到每个等高线都不包含多个代表山脊的等高线。其中重心的变量是用一维数组加偏移地址的方法，每一个三维网格点可以用网格块编号和ijk指标来计算其在一维数组中的偏移地址。

5 运行结果及测试

对于同一等高线，如果不采用放样建模，而直接用得到的等高线曲线利用三角网建模方式，得到的山体在转折处表现过硬，三角面的菱角明显。通过实验比较可以看出，采用等高线建模的山体表面光滑，特别是在山脊等坡度过度处光滑性较好，同时能更好地在三维软件中贴图和植物模型的分布上提供平整的UV分布，从山体植被来说放样建模方法更真实准确地反映了山体的真实几何形态。同时三角网建模方式的面数较多，在正常运算中，往往是将一个四边形直接拆分成2个三角形，所以通过对局部的等高线进行试验看出等高线建模的四边形面数要小于三角网建模的三角形面数的一半。建模后的山体导入虚拟现实软件中后，在没有植被的情况下通过测试运行。如表1所示，三角网建模的山体和放样建模的山体在帧速率的比较下明显不同。

表1 不同建模方式比较

6 结语

通过等高线的一系列处理得到的山体模型是四边面模型，为贴图提供极大的方便，也可以根据四边面的UV分布将模型表面赋予植被。四边面模型在虚拟现实系统中运行良好，尤其是山体与大坝的结合面可以良好焊接，使水电站虚拟现实系统在运行中减少破面和漏面现象。

［1］Miles R E.Probability distribution of a network of triangles（a solution to problem 67－15）［J］.Society for Industrialand Applied Mathematics，1969，11（3）：399－402.

［2］Wu Xiaobo，Wang Shixin，Xiao Chunsheng.A new study of Delaunay triangulation creation ［J］.Acta Geodaetica et Cartographica Sinica，1999，28（1）：28－35.

［3］Lawson C L.Mathematical SoftwareⅢ［A］.Rice J.Software for clsuface interpolation［C］.Pasadena，California：California Institute of Technology，1977：161－194.

［4］Shamos M I，HoeyD.Closest－pointproblems［A］.IEEE Computer Science.Proceeding of the 16th Annual IEEE Symposium on Foundation of Computer Science［C］.Los Angeles.California：IEEE，1975：151－162.

［5］Leberl F，Olson D.Raster scanning for operational digitizing of graphical data［J］.Photogrammetric Engineering and Remote Sensing（S0099－1122），1982，48（4）：615－627.

［6］Greenlee D.Raster and vector processing for scanned linework［J］.Photogrammetric Engineering and Remote Sensing（S0099－1122），1987，53（10）：1383－1387.