多元线性回归系数的图形解析

北京大学生育健康研究所(100191) 李宏田

线性回归分析(linear regression analysis)是研究事物之间线性关系最常用的统计分析方法之一，据自变量数目是否单一可分为简单线性回归分析(simple linear regression)和多元线性回归分析(multiple linear regression)。简单线性回归的数学模型简单，回归直线形象直观，回归系数的解释也通俗易懂。多元线性回归的数学模型及变量间的关系相对复杂，其回归系数常被解释为“在固定其他自变量或扣除其他自变量影响时，Xi每改变一个单位时应变量Y的平均变化量”。但究竟如何固定或扣除，以及扣除的回归贡献的去向，各类参考书籍中少有提及。笔者以郑俊池教授制作的多元线性回归教学模型(图1)为基础，剖析了多元线性回归与简单线性回归函数图像的空间投影关系，进而给出了有关多元线性回归系数固定或扣除含义的图形解释〔1〕。

1．知识回顾

简单线性回归方程^Y=b0+b1X1的回归系数b1指自变量X1每改变1个单位时Y的平均变化量，其函数图像是截距为b0、斜率为b1的直线。多元线性回归方程^Y=b0+b1X1+b2X2+…+bnXn的回归系数b1指固定X1以外的其他自变量或扣除X1以外的其他自变量影响后，X1每改变1个单位时 Y的平均变化量〔2，3〕，仅含2个自变量的多元线性回归方程的函数图像是一个回归平面，含3个及以上自变量的多元线性回归方程难于用函数图像表示。

2．含2个自变量的多元线性回归方程的图示

本文以制作三维模型时所用的回归方程(Y=2+1.33X1+0.20X2，假定完全拟合)为例，给出了仅含2个自变量的多元线性回归方程的示意图(图2)。当X1=0时，回归方程变为Y=2+0.20X2，其图形为X2轴与Y轴所确定的平面内的直线OB;当X2=0时，回归方程变为Y=2+1.33X1，其图形为X1轴与Y轴所确定的平面内的直线OA;当X1=X2=0时，回归方程变为Y=2，其图形即为点O。据以上分析可知，含2个自变量的多元线性回归方程的图形即为等截距(OO″)、定斜率(多元线性回归方程的回归系数)的两条简单回归直线所确定的回归平面。满足回归方程的任何一点(X1，X2，Y)，如图 2 中的 M(3，5，7)点，均应位于平面AOB上。

图1 多元统计教学模型

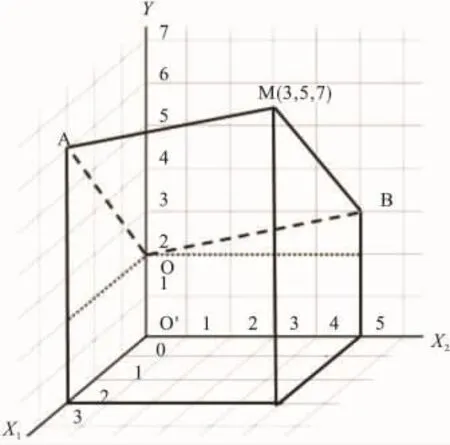
图2 回归方程Y=2+1.33X1+0.20X2函数图形(AOBM)

图3 回归方程Y=2+1.33X1+0.20X2函数图形解析

3．投影、固定和扣除

图2中M点在X1轴与X2轴所确定的平面内的投影为M'(3，5，0)点(图3)，M 点的含义可解释为当X1=3、X2=5时，全部自变量(含截距)对应变量Y的总回归贡献大小为7(MM')，其中截距的贡献量为2(OO')，X1的贡献量为 4(AA0)，X2的贡献量为 1(BB0)。由解析几何知识可知平面AA'O'O平行于平面MM'B'B，故直线OA与BM永不相交;又因OA和BM同在平面OAMB内，故OA恒平行于BM;那么BM在X1轴与Y轴所确定的平面内的投影B″M″也恒平行于OA。由以上分析可知，不论X2取何值，只要其取值固定，BM在X1轴与Y轴所确定的平面内的投影的斜率都不会改变，且恒等于直线OA(X2=0)的斜率，故X1的回归系数可解释为“在其他自变量(X2)固定时，X1每改变一个单位时应变量 Y的平均变化量为1.33”。尽管X2取不同值时，BM在X1轴与Y轴所确定的平面内的投影的斜率不变，但对比(X1=3，X2=5)时 Y=7(MM')和(X1=3，X2=0)时 Y=6(AA')可知，因X2取值改变(由5变为0)而被扣除(X2=0，即X2的贡献被扣除)的贡献量实为BB0或OB″，故据此X1的回归系数亦可解释为“在扣除其他自变量(X2)的影响(即贡献量)后，X1每改变一个单位时应变量Y的平均变化量为1.33”。同理，因X1取值改变所致的扣除情况与此类同，本处从略。

4.讨论

本文通过对比仅含2个自变量的多元线性回归方程的函数图像与相应的简单线性回归函数图像的几何关系，形象直观地阐明了有关多元线性回归系数固定、扣除作用的具体含义，并对扣除的回归贡献进行了几何定位，对于正确理解多元线性回归乃至其他多元回归系数的含义有一定的参考价值。

(致谢:笔者有幸师从郑俊池教授，在郑教授的指导下撰写了此文。郑教授于20世纪90年代初制作了该模型(图1)，并用于医学研究生多元统计教学，效果极好。

1．李竹，郑俊池主编．新编实用医学统计方法与技能．北京:中国医药科技出版社，1997:137-148．

2．金丕焕主编．医用统计方法(第2版)．上海:复旦大学出版社，2003:309-316．

3．陈峰主编．医用多元统计分析方法．北京:中国统计出版社，2000:30-31．