医学统计学位课程考试项目分析*
山西医科大学公共卫生学院(030001) 徐 琳 张岩波 郑建中
考试是学校教育中的一个重要的组成部分。对考试试卷进行科学有效的分析评价,不仅可以检验教学效果、评估教学质量,还可以提高命题及组卷水平,在教与学各方面都具有十分重要的意义。科学有效的试卷质量分析评价要运用教育测量与考试有效性研究方面的专业知识。项目分析(item analysis)是基于经典测验理论(classical test theory)的一种常用的试题分析和评价方法。项目分析的量的分析就是通过计算项目的一些统计量作为项目质量高低的指标,进而挑选和修改题目〔1〕。本文将运用经典测验理论,对山西医科大学2008级硕士研究生医学统计学位课程考试的502份试卷进行项目定量分析,为评价试题质量提供依据。
项目分析指标
1.难度
难度(difficulty)即测题的难易程度。难度的计算公式:P=N/M,其中P为题目难度,N为该题目的得分均值,M为该题目的满分值。难度实际高低与难度值大小刚好相反,难度高的题目其难度值反而小,而难度低的题目其难度值却大。
由于选择题有猜题的可能,对于多选一的选择题而言,其难度的计算要用校正公式:CP=(KP-1)/(K-1),其中CP为校正难度值,P为用难度公式直接计算得到的难度值,K为选择项的数目。运用校正公式计算出的难度值,可以直接进行比较,因为在计算中已经考虑了选择项数目不同对猜题的影响。
2.区分度
项目区分度(item discrimination)即测题将受测者实际能力水平区分鉴别开的能力。项目区分度有多种计算方法,如积差相关法、点二列相关法、二列相关法、四分相关和φ相关、因素分析法、极端组法等。项目区分度的计算最常用的是鉴别度指数(也称D指数),是极端组法中的一种计算方法。
鉴别度指数的计算:根据测验总成绩将受测者从高分到低分排列,选取前27%的受测者(或25% ~33%)作为高分组,再选取最后27%的受测者作为低分组,分别计算出高分组和低分组的难度值,最后代入公式D=PH-PL计算出鉴别度指数。其中D为鉴别度指数,PH为高分组难度值,PL为低分组难度值。在选取高分组和低分组的受测者人数方面没有严格的规定,出于计算简便的目的,可灵活掌握,但要两组人数相等。
3.难度与区分度的关系
项目区分度受难度的影响,控制试题难度可以提高项目的区分度。当测验过于难,实际能力高的受测者和实际能力低的受测者都未得分,则无区分度可言;当试题过于容易,实际能力高的受测者和实际能力低的受测者都能得分,也无区分度。过难和过易的试题,都会降低项目区分度。当难度值为0.5时,试题的区分度为最好。在命题及组卷时,不同题目的难度均有不同,所有题目的难度值可控制在一定范围内。实际能力水平不同的受测者对不同难度的测题表现出不同的区分度。
4.运用项目分析指标衡量试题质量
(1)运用难度衡量试题质量
在命题及组卷时,要尽力做到题目的平均难度为0.50左右,并且做到各个题目的难度值在0.20~0.80范围内。

表1 项目难度优劣的判断标准
测题难度应符合考试目的,难度高的测题适用于选拔性考试,难度低的测题适用于达标性考试。
(2)运用区分度衡量试题质量
有些时候进行试卷分析为避免大量的数据计算,仅在大题下作区分度分析,熊广兴〔2〕认为从区分度这一指标用以鉴别、筛选题目的功能来说,应对试卷中每一道小题进行分析,仅对大题计算区分度会夸大题目的鉴别力〔3〕。
测量学家伊贝尔(R.L.Ebel)提出了判断测题优劣的项目鉴别度标准,见表2。
0.30以上的鉴别度指数反映试题具有良好的区分功能,鉴别度指数在0.20~0.30之间的项目可依据测验要求灵活掌握,适当保留。

表2 项目鉴别度优劣的判断标准
(3)综合难度、区分度衡量试题质量
综合难度(P值)、区分度(D值)衡量试题质量,可分为以下 A、B、C、D 四级。
A:P 值 >0.5,D 值 >0.20,试题难度适中,区分度良好,是好试题。
B:P 值 <0.5,D 值 >0.20,试题偏难,但区分度良好,依然适用。
C:P 值 >0.5,D 值 <0.20,试题容易且区分较差,必要时少用。
D:P 值 <0.5,D 值 <0.20,试题既难又无区分能力,不应参加计分。
5.多重选择题的干扰项分析
选择题的作答除了会受到猜题的影响,还会受到选项中其他干扰项的影响,因此对选择题的干扰项进行分析是十分必要的。对于干扰项也有其难度分析和区分度分析。干扰项的难度分析是分析其对受测者诱惑性的大小,对于一个干扰项来说,选择这个干扰项的人数多少可反映其诱惑性的大小。干扰项的诱惑性要适中,不能诱惑性太强,使选择它的人数过多;也不能诱惑性太弱,起不到干扰作用。干扰项的区分度类似项目的区分度〔4〕。理想的区分度较高的干扰项,能产生使实际能力水平高的受测者选择正确选项的比例大于实际能力水平低的受测者的效果,并且不出现负向干扰项,即不出现实际能力水平高的受测者选择错误干扰项的人数多于实际能力水平低的受测者的情况出现。
实例分析
本研究以山西医科大学2008级硕士研究生医学统计学位课程考试的502份试卷为例。考试题型:判断题10个,每题2分;单选题10个,五选一,每题2分;简述题2个,第1题8分,第2题12分;分析计算题4个,每题10分。根据总成绩把受测者分为高分组和低分组(按照27%选取),每组136人。采用自编Excel试卷分析模板,主要结果见表3~表5。
1.试题分析一般情况
表3可见,试卷总体难度中等,判断题、单选题较易,简述题、分析计算题难度中等。试卷总体鉴别度指数偏低,以判断题的区分度最差。综合判定,试卷总体为A级,是好试题;但判断题容易且区分较差,为C级。

表3 试题分析一般情况
2.每小题的难易度与区分度分析
表4中选择题的难度采用了校正难度系数CP,结果可见:34个项目的难度指数范围在0.068~0.958之间,平均为0.72。其中分析计算题4(4)的难度值为0.068,为最难项目;单选题10的难度值为0.958,是最容易项目。在命题及组卷时,要尽力做到题目的平均难度为0.50左右,并且做到各个题目的难度值在0.20~0.80范围内。本研究的34个项目中,有14个项目的难度值大于0.80,有1个项目的难度值小于0.20,该测题总体难度中等。结合本次测题目的,并非为选拔少数能力高的被试,故此难度适中。
从区分度角度分析,34个项目中,单选题2、单选题4、单选题7、简述题1、分析计算题3这5个项目的鉴别度指数达到0.40以上,是非常优良的项目。判断题1、判断题2、单选题1、分析计算题1(3)这4个项目的鉴别度指数在0.30~0.39之间,是良好、如能修改更好的项目。判断题4、判断题9、单选题5、单选题6、单选题8、简述题2、分析计算题1(2)、分析计算题2(1)、分析计算题2(4)、分析计算题4(2)、分析计算题4(3),这11个项目的鉴别度指数在0.20~0.29之间,是尚可、仍须修改的项目。0.30以上的鉴别度指数反映试题具有良好的区分功能,鉴别度指数在0.20~0.30之间的项目可依据测验要求灵活掌握,适当保留。其余14个项目的鉴别度指数在0.19以下,是劣、必须淘汰的项目。
34个项目综合判定,A级的有19个,是难度适中、区分度良好的好试题;B级的有1个,试题偏难,但区分度良好,依然适用;C级的有11个,试题容易且区分较差,必要时少用;D级的有3个,试题既难又无区分能力,不应参加计分。
3.单项选择题干扰项分析
有10题,每题有4个干扰项,共40个干扰项。其中,单选题3的E选项无论对高分组还是低分组都缺乏诱惑性,没有被受试者选择。这一干扰项未起到应有的干扰作用,可能干扰作用太明显,缺乏诱答性,应加以修改和替换。这种无干扰作用的选项,使受试者猜题成功的可能性增加。40个干扰项中,没有出现负向干扰项,即没有出现高分组选择错误干扰项的人数多于低分组的情况出现。对于单选题3、9、10这三题来说,高分组和低分组选择正确选项的受测者人数相差不多,应增加三题中其余选项的诱惑性,以增大干扰作用。
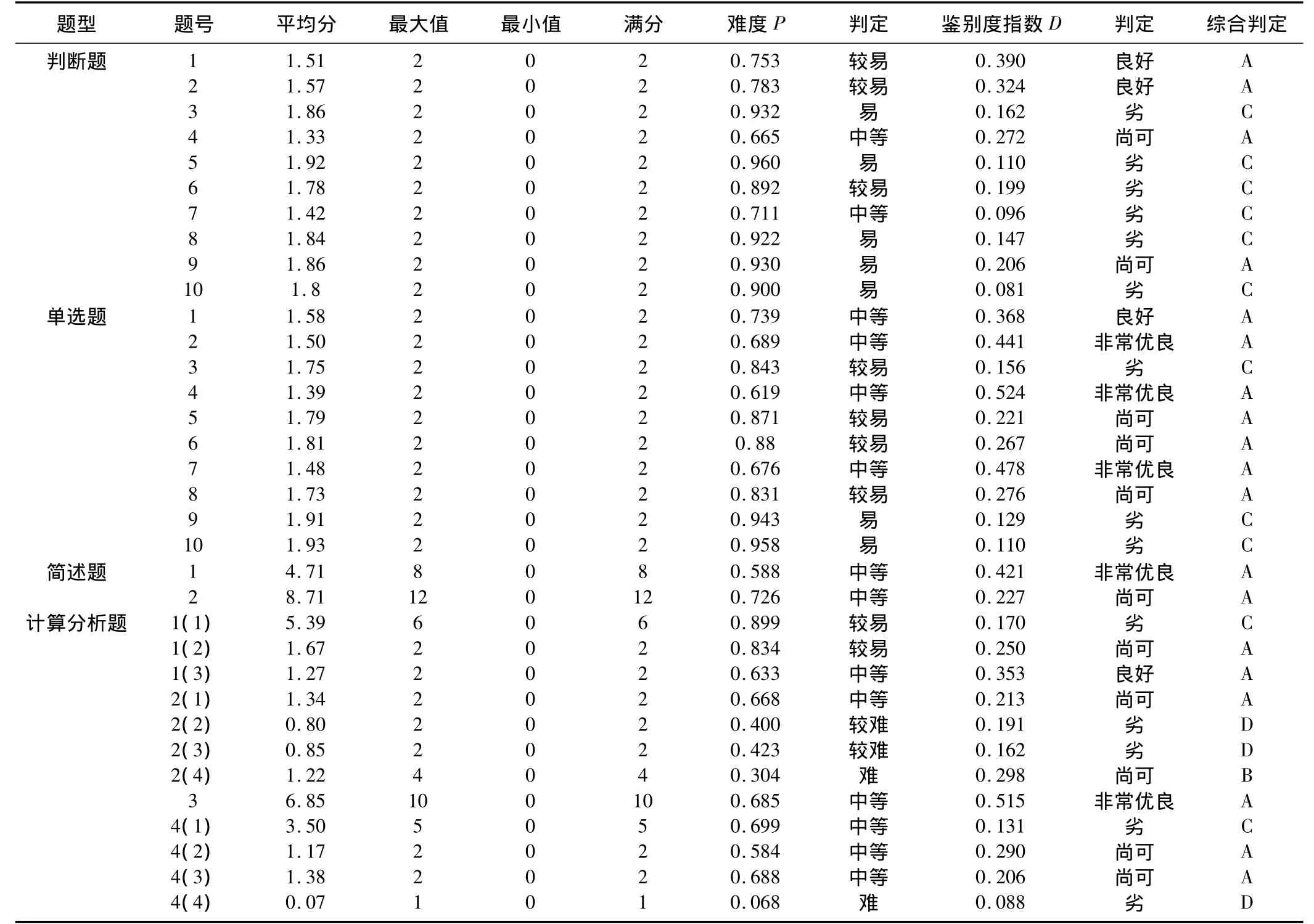
表4 每小题的难易度与区分度

表5 10道单选题干扰项分析结果
总结与讨论
通过对考试试卷难度和区分度的分析,可以看到试卷分析的重要性。命制一份质量高的试卷很不容易,只有掌握试卷分析的相关知识,并将其应用在教学工作中,才能命制出高质量的试题。
本文的实例分析中,选择题难度的计算采用了难度校正公式计算CP值的方法。虽然本文分析的试卷仅涉及五选一这一种单选题题型,难度值校正与否均不影响本文结果;但对于今后进行其他试卷评价时,会遇到在同一试卷中有多种单选题(如三选一、四选一、五选一)题型的情况,那时计算CP值后直接作比较,就能更好地体现出CP值在考虑选择项数目不同对猜题影响方面的价值。
自上世纪20年代经典测量理论引入我国,在近90年的传播应用过程中,逐渐发展成为简单明了、应用广泛、容易掌握和操作的较为完善的统计分析方法。但经典测量理论也有其不足之处,所求得的题目参数(难度、区分度)受所选取样本大小和能力水平的不同而有差异。与经典测量理论相比,项目反应理论是一种较新的教育与心理测量理论,如最常用的rasch模型可更好地评价考生能力,同时也可以删除或修改试题,提高评分方案的准确性。但该理论的理解和掌握均有一定的难度,不利于普及,其应用受到限制。
1.郭庆科.心理测验的原理与应用.北京:人民军医出版社,2002:82-89.
2.熊广星.心理与教育测量若干概念的应用问题.广西师范大学学报(哲学社会科学版),2000,36(3):63-65.
3.黄颖,林端宜.试卷分析研究现状综述.西北医学教育,2005,13(1):39-40.
4.左天明,刘强,张阳.用Rasch分析法初步考察计算机模拟病例的评分项目.中国卫生统计,2008,25(3):299-301.

