煤矿巷道固定照明灯节能优化安置分析

余 旭，徐宾泽，罗 夏

（中国矿业大学 安全工程学院，江苏 徐州 221116）

1 引言

煤矿井下照明是矿井安全生产的重要保证，井下照明一般有两种形式。一种是移动式照明，如工人佩戴的矿灯；另外一种是固定式照明，比如一些主要巷道中的防爆荧光灯、白炽灯。我国目前在巷道固定照明安装上随意性较大，在生产安全和节能减排方面均有不少问题。

在我国煤矿井下主要运输巷道的照明灯具配置多荧光灯或者白炽灯,灯具规格多为20W。一盏20W的荧光灯,功电耗在25W左右，有的矿井安装距离超过100m。其照度严重不符合国家矿山安全的规定，研究表明，工业场所照明质量越差，事故发生率越高。所以在这种照明条件下，很容易发生事故。同时一旦发生事故也不适合人员的安全逃生。而有的矿井为保证安全，巷道照明中照明设备安装分十几种，井下大巷几乎灯火通明。这对节能减排来说也是十分不利的。

所以文章将针对这些问题，提出一种井下巷道固定照明设备的优化安置方案，既保证矿井的安全生产，又能取得良好的节能的效果。这对于我国的低碳经济是十分有利的。

2 我国煤矿井下照明标准

提倡井下照明节能是在保证井下工作对照明质量的前提下，力求减少照明系统中能量损失，最有效地利用电能。按照《国家照明设计标准》，照明设计取值单位是照明功率密度值（LDP），即是单位使用面积的照明总安装功率密度（W/m2）。我国在《国家金属非金属矿山安全规程》中对井下固定照明做了相关要求，井下固定照明要满足表1要求。

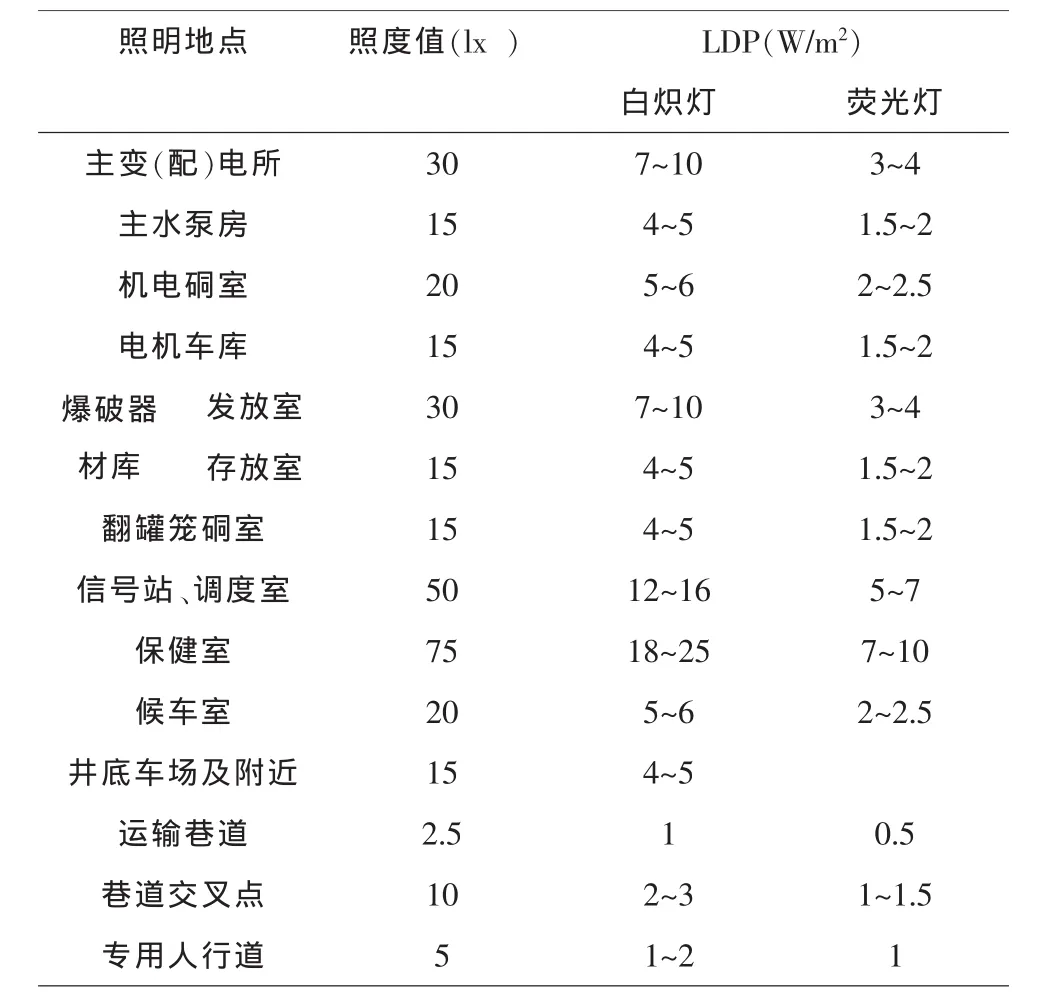
表1 井下固定照明及照度标准表

需要指出的是LDP及照度值和照明灯具种类、规格及安装距离有关系，如照明灯具相隔100m,灯具采用300W白炽灯，经计算井下LDP是1.2W/m2，如果采用65W的节能灯，40m间距安装1个灯具，井下LDP是0.65W/m2,是原设计标准的54%。所以在进行优化方案时要综合考虑这三方面的结果。

3 巷道中荧光灯的优化安置

数学模型是科学研究的重要手段，它能将实际问题简化上升到理论高度，以数学求解的方式，得出研究结果。在通过假设条件，建立数学模型，从而得到优化结果时，作如下符号规定:P为荧光灯灯功率，h为灯的高度，r为荧光灯到任意一点的距离，L为巷道的宽度,C0为正常工作时的最小照明强度值，l为灯间距。

（1）两盏荧光灯研究巷道中荧光灯之间最大的灯间距优化方案。对于采用大功率长距离照明时井下巷道固定照明可简化为图1所示模型。灯间距优化目的是在路灯之间的照明效果相同条件下，确定荧光灯之间的最佳距离l。

图1 巷道井下照明简化图

（2）巷道内一排荧光灯优化方案。对于采用小功率长多盏灯同时照明时可以简化为图2所示模型。其中，路灯B和C之间的路段，与中点Q相对的R点的照明强度最小，并且计算该点照明强度时，只需考虑灯A、B、C、D对其的影响，其他较远的路灯对其的影响可忽略。

图2 巷道井下一排荧光灯照明简化图

图3 考虑边界时灯间距确定模型

（3）考虑边界时灯间距的确定。考虑边界时灯间距的确定可根据以下模型进行计算（见图3）。

4 结论

文章从煤矿巷道节能灯安置的细节入手，在保障巷道内正常的照明情况下，通过合理假设，科学论证，进行优化照明灯的安置位主要得到如下结论：

（1）通过建立数学模型，得到了井下照明采用大功率照明时，两盏照明灯合理间距的计算方法。

（2）在得到两盏灯合理间距计算方法的基础上，通过建立数学模型，得到了采用小功率荧光灯多盏灯同时照明时灯间距布局的计算方法。

（3）为避免井下照明留死角，建立了井下照明边界确定的数学模型，并得到了合理的灯布局方法。