基于VaR风险约束下保险公司的最优混合投资策略

赵 武，王定成，2，1b，曾 勇

(1.电子科技大学 a.经济与管理学院；b.应用数学学院，成都 610054;2.澳大利亚国立大学 金融数学中心，堪培拉，ACT 0200)

0 引言

众所周知，保险公司的成功运营不仅依赖于其保险业务，而且依赖于其投资业务。这样保险公司既面临着金融市场潜在损失的风险，还面临着高额保险索赔的风险。结果，综合考虑金融市场的动态变化以及保险过程还有两者相互作用的聚合风险模型是十分必要的。自从 F.Lundberg在齐次复合泊松过程索赔的基础上建立聚合风险模型以来，精算界一直把破产概率作为保险公司的风险度量。在经典的破产理论中，Gerber[1]和Feller[2]对保险公司的盈余用随机过程建模，分别利用了鞅方法和更新方法得到了破产概率的指数型上界。并且如果索赔额大小具有指数矩，那么破产概率随初始资本金呈现指数衰减，关于经典结果的详细讨论可以参考卡尔斯等[3]。经典结果的一个重要的推广途径就是考虑保险公司把盈余投资到利率为常数的无风险债券上，Klüppelberg& Stadtmüller[4]考虑了这种模型，得到了当索赔额大小具有规则变化尾的情形下，随着初始资本金的增大，破产概率和索赔额的尾部有着同样的衰减速度；Sundt&Teugels[5]得到了破产概率对于初始资本金的一致上界；Tang[6]讨论了索赔到达过程为一复合泊松过程时有限时间破产概率问题；Wang[7]将Tang[6]的结果推广到索赔到达过程为更新过程的情形。

Paulsen&Gjessing[8]首先研究了保险公司的投资问题，但只是考虑了将所有的盈余投资到风险资产上，而没有考虑投资组合问题；Browne[9]考虑了保险公司的承保盈余过程是带漂移的布朗运动，风险资产是几何布朗运动的模型，得到了风险资产的投资应该与初始资本金无关，并且恒为常数，但是显然模型不满足聚合风险模型通常的假设，即复合泊松过程的假设；Hipp&Plum[10]建立了保险公司的承保盈余过程为复合泊松过程的模型，得到了最大化生存概率的HJB（Hamilton-jacobi-Bellman）方程。Gaier et.al[11]在索赔额具有一致指数矩的假设下，得到了一种常数的投资策略，并在这种常数投资下，估计出破产概率的Lundberg上界。

本文同样考虑保险公司的投资策略问题，与以往的文献不同的是，用在险价值（VaR Value-at-Risk）而不是破产概率去衡量保险公司的风险，在险价值是重要的金融风险管理工具之一,在国际上已获得广泛认可。VaR的优点在于概念简单直观、计算方便且易于实施。可将其定义为在一定的持有期及一定的统计置信度内，某一金融工具或投资组合所面临的最大潜在损失的估计值。对于风险资产的价格，本文用指数Lévy过程进行建模1。在本文的第二部分，假设保险公司采取混合投资策略，我们对保险公司的总资产过程建立模型，在此基础上给出最优化模型可以使VaR限制在一定的水平下，保险公司总期望财富最大。第三部分给出模型求解。

1 模型的建立

首先介绍经典的Cramér-Lundberg风险模型。记保险公司在时刻的承保盈余过程为，

就称分布函数为一有正则变化尾的分布，具有尾指标-α＜0，记为FX(x)∈R-α.很多著名的重尾分布都具有正则变化尾，如帕累托分布，逆Gamma分布等。

接下来给出混合投资策略的定义，参见Emmer et.al[12]。混合投资策略是指在每一个时间点上投资总财富的固定比例的份额到风险市场上，剩下的用来购买无风险债券。假设保险公司投资到一个 Black-Scholes型的市场，该市场由股票和无风险债券组成。债券和股票的各自的价格过程如下：

对（2）中的两式分别微分，得：

在每一个时刻点上把总资产的一个固定比例投资风险市场，剩下的1-θ投资到无风险市场上。本文不考虑保险公司卖空风险资产和借贷，所以θ∈[0,1]。虽然为常数，该投资组合策略是一个动态策略，因为保险公司的总资产过程是不断变化的，保险公司要不断的调整投资组合头寸。被称为投资策略。Lévy过程L(t)的特征三元组为(γ,σ2,v)。定义ε(L)被定义成下面微分方程的解

过程Z=ε(L)被称为过程的随机指数或称为Doléans-Dade指数。Cont&Tankov[13]中证明了ε(L)的存在唯一性。

综合以上假设，保险公司的总资产过程满足以下随机微分方程：

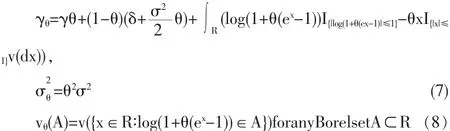
Lθ的Laplace指数如果存在，可以表示为φ(θ,s)=logE[e-sLθ(A)]。从Kostadinova[15]中引理5.3.1可以得出，如果0＜E[L(1)]＜∞，σ＞0或者v((-∞,0))两者成立其一，对于θ∈(0,1)，一定存在唯一的正数κ=κ(θ)＞0使得φ(θ,κ)=0。

定义保险公司的折现净损失过程如下：

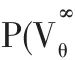
其中β∈(0,1)是一个小概率值，代表着很高的置信水平。我们要解决的是如下的最优化问题：

其中：C＞0，T＞0

根据有限时间破产概率的定义：

ψ(u,T)=P{Vθ(t)＞u}，对于某个0≤t≤T}等价地，有：

根据（13），最优化问题（11）等价于：

由（14）可知，最优化模型（11）中的VaRβ()的经济解释为：如果保险公司要在时间之前破产的概率不超过，所需准备的最少的初始准备金。

2 模型的求解

由于最优化模型（14）的复杂形式，几乎是不可能找到模型的解析解，我们的目标是找到模型的近似解法。Heyde& Wang[16]针对该模型，假设索赔额具有正则变化尾，即FX(x)∈ R-α，研究了有限时间破产概率，并得到了破产概率的尾渐进等价式。本文利用其结果，给出最优化模型（14）的近似最优解。

令θ*为最优的投资策略，下面给出定理1。

定理1.假设安全负荷条件2成立，即c-λE(X)＞0。还假设φ(-1)＞δ。如果索赔额服从连续型分布，且FX(x)∈R-α。那么，对于任意固定的T＞0和充分大的u，最优化问题（14）解为

其中θ2是方程J（φ(θ,α)）≥(C)的两个解中较大的那个解。

如果条件φ(α+1)+δ＜φ(α)成立，J（φ(θ,α)）在区间θ∈[0,1]单调递增，且：

证明：参考Kostadinova[15]中的引理3.4.4，如果c-λE(X)＞0和φ(-1)＞δ成立，那么E[Uθ(T)]关于θ递增。因此，最优化模型（14）等价于：

接下来要考虑的就是对式（18）求解。

根据Heyde&Wang[16]中的定理1,如果FX(x)∈R-α，那么对于固定的T＞0：

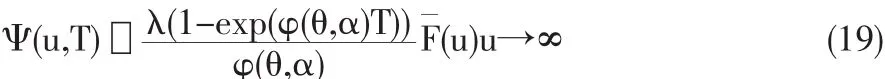
对于充分大的，把（19）代入（18），可得：

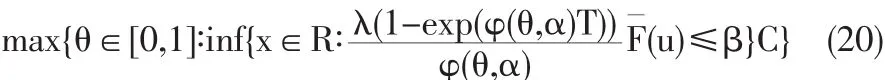
因为exp(φ(θ,α)T))-1和φ(θ,α)同号，而且(u)连续且递减，所以有：

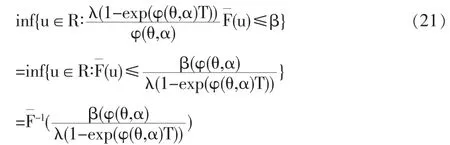
下一步，考虑φ(θ,α)的性质，由Kostadinova[15]给出的引理3.2.5，φ(θ,α)是关于θ的严格凸函数。如果φ(-1)＞δ成立，那么：

我们可以找到φ(θ,α)的极值点θ＾，由（7），可以算出：

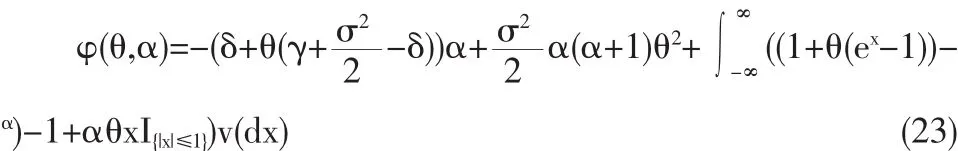
对φ(θ,α)求一阶导数，有：

如果∂/∂θφ(1,α)≥0，等价于α(α+1)+δ≥φ(α)成立，那么φ (θ,α)的极小点θ＾∈[0,1]，反之α(α+1)+δ＜φ(α)成立，φ(θ,α)在区间θ∈[0,1]单调递减。对J(φ(θ,α))求导

图1 J(θ)的图形（φ(1,α)+δ(α)）。

图2.的图形（φ(α+1)+δ＜δ(α)）

图1表示了条件（φ(α+1)+δ≥δ(α)）成立的情形，这时θ*=θ2；图2表示了条件φ(α+1)+δ＜δ(α)）成立的情形，这时θ*=1。

最后给出具体的数值例子阐述上述结果。参数的设定保证三个例子的股票收益的期望和方差都相等，且E[L(1)]= 0.5，Var[L(1)]=2。设定λ=0.2，c=2，C=15。索赔额服从参数为的帕累托分布。下面考虑三个具体的Lévy过程：

模型 1（几何布朗运动）：假设股票的对数收益率为L(t)= at+bW(t)。其中a=0.2,b=0.5。

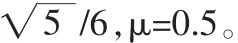
模型3（VG Lévy过程，madan&Seneta[18]）：L(t)=μt+W(V (t))。其中μ＞0，W是一个布朗运动，飘移率为a，波动率为b。V(t)是一个和过程独立的gamma Lévy过程，V(1)具有Gamma分布，其密度函数为：

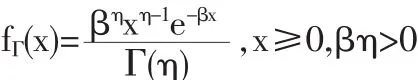
V(t)的特征三元组为(0,0,vΓ)，vΓ(dx)=I{x＞0}ηx-1e-βxdx。L的Lévy测度为：

令β=η=4，μ=0.2，a=0，b=0.5。

根据定理1，可以分别计算上述三个模型的最优投资比例，由下表给出。

表1 最优投资比例

4 结束语

在聚合风险模型的基础上，本文考虑了保险公司的投资问题，假设保险公司在Black-Sholes型的市场上进行投资，投资策略采用混合投资策略，即将全部资产按固定比例分别投资于股票市场和无风险债券。假设股票价格服从指数Lévy过程，同时索赔额服从重尾分布，在此基础上对保险公司的总资产过程进行建模。利用VaR方法建立了保险公司的最大风险承受能力与最优投资比例之间的关系。最后利用破产理论给出了最优投资比例的近似最优解，该最优投资比例可以在VaR限制在一定水平下可以使保险公司的期望财富最大。

[1]Gerber,H.U.，成世学，严颖译.数学风险论导引[M].北京：世界图书出版发行公司，1997.

[2]Feller,W.An Introduction to Probability Theory and Its Applications.[M].New York:John Wiley Sons,1971.

[3]R.卡尔斯,M.胡法兹,J.达呐,M.狄尼特.现代精算风险理论[M].科学出版社,2005.

[4]Klüppelberg C,Stadtmüller U.Ruin Probabilities in the Presence of Heavy-Tails and Interest Rates[J].Scand.Actuarial J.，1998，(1).

[5]Sundt B,Teugels JL.Ruin Estimates under Interest Force[J].Insurance:Mathematics and Economics,1995,16(1).

[6]Tang Q.The Finite Time Ruin Probability of the Compound Poisson Modelwith ConstantInterestForce[J].J.Appl.Probab.，2005,42(3).

[7]WangDC.Finite-Time Ruin Probability with Heavy-Tailed Claims and Constant Interest Rate[J].Stochastic Models,2008,24(1).

[8]Paulsen J,Gjessing HH.Ruin Theory with Stochastic Return on Investments[J].Advances in Applied Probability，1997,29(4).

[9]Browne S.Optimal Investment Policies for a Firm with a Random Risk Process:Exponential Utility and Minimizing the Probability of Ruin[J].Mathematics of Operations Research,1995,20(4).

[10]Hipp C,Plum M.Optimal Investment for Insurers[J].Insurance: Mathematics and Economics,2000,27(2).

[11]Gaier J,Grandits P,Schachermayer W.Asymptotic Ruin Probabilities and Optimal Investment[J].Ann.Appl.Probab,2003,13(3).

[12]Emmer S,Klüppelburg C,Korn K.Optimal Portfolioswith Bounded Capital-at-Risk[J].Math.Finance.，2001，(11).

[13]Cont R.，Tankov P.Financial Modeling with Jump Processes[M]. New York:Chapman&Hall／CRC，2004.

[14]Klüppelberg C，Kostadinova R.Integrated Insurance Risk Mod els with Exponential Lévy Investment[J].Insurance:Mathematics and Economics,2008,42(2).

[15]R.Kostadinova.Optimal Investment for Insurers when the Stock Price Follows an Exponential Lévy Process[J].Insurance:Mathematics and Economics,2007,41(2).

[16]Heyde CC,Wang DC.Finite-time Ruin Probability with an ExponentialLévy ProcessInvestmentReturn and Heavy-tailed Claims[J].Adv.in.Appl.Probab，2009,41(1).

[17]Kou SG.A Jump-diffusion Model for Option Pricing[J].Management Science,2002,48(8).

[18]Madan D,Seneta E.The Variance Gamma(VG)Model for Share Market Returns[J].Journal of Business，1990，63(4).