运用Gibbs抽样解决数据缺失

王 怡，周 力

（东华大学 旭日工商管理学院,上海 200051）

1 传统缺失值处理方法

目前国内广泛接受的对于数据仓库缺失值处理方法有6种处理缺失值的方法：

(1)忽略元组：当缺少类标号时通常这样做（假定挖掘任务涉及分类）。除非元组有多个属性缺少值，否则该方法不是很有效。当每个属性缺少值的百分比变化很大时，它的性能特别差。

(2)人工填写缺失值：一般，该方法很费时，并且当数据集很大，缺少很多值时，该方法可能行不通。

(3)使用一个全局常量填充缺失值：将缺失的属性值用同一个常数 （如 “Unknown”或-∞）替换。如果缺失值都用“Unknown”替换，则挖掘程序可能误以为它们形成了一个有等趣的概念，因为它们都具有相同的值“Unknown”。因此，尽管该方法简单，但是它并不十分可靠。

(4)使用属性的均值填充缺失值。

(5)使用与给定元组属同一类的所有样本的属性均值。

(6)使用最可能的值填充空缺值：可以用回归、基于推导的使用贝叶斯形式化方法或判定书归纳确定。

方法3～6由于没有使用总体的信息，可能致使数据偏置，不能正确的反映数据总体情况。另外，虽然方法6目前最为常用，因为与其他方法相比，它使用现存数据的多数信息来推测空缺值，如果所有有关系的值均缺失，无法根据现有值产生其他值的情况，方法6也就失效了。因此可以说目前提出的方法并不能很好的解决数据缺失的问题。

总而言之，虽然目前已经提出了一些应用于数据预处理的方法，但是在对缺失数据进行处理的问题上都没有理想的解决办法。因而本文将对以上两个问题的解决进行探讨，下面就对研究思路和研究内容进行详细阐述。

2 Gibbs抽样基本步骤介绍

Gibbs抽样是一种潜在应用非常广泛的仿真工具，1990年该工具发表后立即得到了广泛的响应。Gibbs抽样表现为一个Markov链形式的Monte Carlo方法，其良好的性质可用于许多随机系统的分析、多元分布的随机数产生。下面介绍Gibbs抽样的基本原理。

假设X,Y等大写字母表示随机变量或随机向量；[X], [Y]则代表其相应的概率分布；[X|Y],[Y|X]表示条件分布。

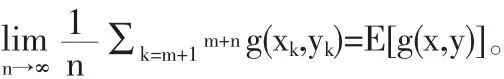
Step 1任意选取X的一个可能取值点x1，根据[Y|X=x1]产生随机数y1，随机数对(x1,y1)成为随机点列{(x,y)n}中第一个点；

Step 2根据[X|Y=y1]产生随机数x2，根据[Y|X=x2]产生随机数y2，随机数对(x2,y2)成为随机点列{(x,y)n}中第二个点；

Step 3重复以上过程n次，我们即能得到所需要的随机点列{(x,y)n}。

推广到一般情况，如果条件分布

需要强调的是，Gibbs抽样的先决条件是部分特定条件分布已知，称为“条件分布充足条件”即FCDC，也就是上面提到的二元情况中的[X|Y]和[Y|X]，以及一般情况中的，[X1,X2,…,Xk]，[X2,X1,X3,…,Xk],…,[Xk,X1,…,Xk-1]。

3 实证分析

（1）数据准备

以某项统计调查学生基本信息的数据作为原始数据，该数据共有300条记录。选择其中学生的性别和家庭情况两列作为Gibbs抽样仿真中的两个变量，这两列的数据是离散的，性别中1代表女生，0代表男生。而家庭条件中1代表单亲家庭，2代表他人照顾，3代表双亲家庭。

将后150条记录的数据去除，造成全数据缺失的情况。去除的数据仍需保存，以便在使用Gibbs抽样后对数据的模拟情况进行评价。

（2）获得条件分布

对信息完整的前150条记录进行统计，利用所得到的统计数据建立条件分布充足条件FCDC，统计数据见表1。

根据表1的数据我们可以看出，在已知家庭情况的条件下，性别服从贝努里分布，即[性别|家庭情况]～Bernoulli。

表1 [家庭情况|性别]条件分布概率

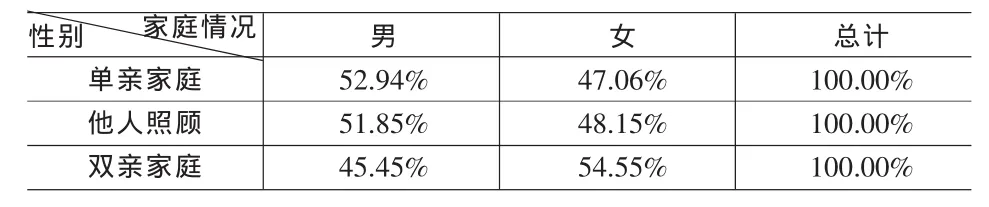
表2 [性别|家庭情况]条件分布概率

表2说明在已知性别的条件下，家庭情况服从三项的离散分布，FCDC条件具备。

（3）仿真数据生成

这里我们使用Excel来实现Gibbs抽样仿真。首先使用rand（）命令产生随机数数列。在Excel中，rand（）产生的是0到1之间均匀分布的随机数，因而所产生的随机数小于0.6的概率就是0.6。

根据性别产生家庭情况仿真数据所使用的命令语句形式如下

=IF(E2=0,IF(D3＜0.48,1,IF(D3＜0.6667,2,3)),IF(D3＜0.4267,1,IF(D3＜0.6,2,3)))

而根据家庭情况产生性别仿真数据所使用的命令语句为

=IF(F3=1,IF(C3＜0.5294,0,1),(IF(F3=2,IF(C3＜0.5185,0,1), IF(C3＜0.4545,0,1))))

（4）仿真结果评价

仿真数据生成好后，需评价仿真效果以证明抽样的优越性。统计情况表3所示。

使用Excel的单因素方差分析，显示结果如表5表6所示。

在表5中，由于F=7.708647＜F0.05(1,4)=7.71，所以接受两组无差异的原假设，说明在家庭情况属性中，原数据与仿真数据无显著性差异。

表3 原数据与仿真数据对比表（家庭情况）

表4 原数据与仿真数据对比表（性别）

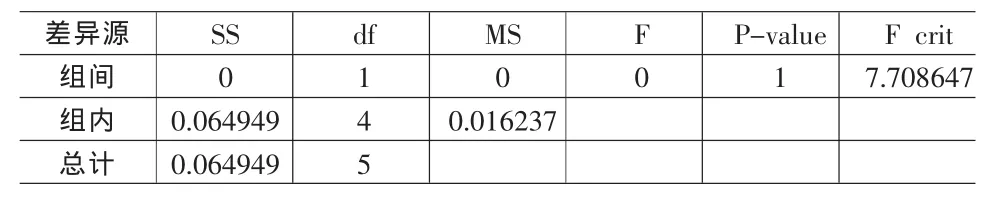
表5 单因素方差分析表显示结果（家庭情况）

表6 单因素方差分析表显示结果（性别）

在表6中，由于F=18.51282＜F0.05(1,2)=18.52，所以也接受两组无差异的原假设，说明在性别属性中，原数据与仿真数据无显著性差异。

由此可见，使用Gibbs抽样对缺失数据进行仿真能获得较好的效果。

4 结论

本文提出了将Gibbs抽样仿真应用到缺失值处理中，改善了以往方法不能考虑总体情况的缺陷，在大样本情况下，能够很好地将已知的总体分布信息纳入到对缺失值的处理当中。

使用Gibbs抽样进行缺失值处理的优势在于以下几点。

首先，Gibbs抽样仿真能够较为理想的处理全数据缺失的问题，当有相关关系属性内数据全部缺失，同样可以通过Gibbs抽样对缺失数据进行填充。这就将Gibbs抽样仿真与传统的回归、贝叶斯推导等方法区分开来。

其次，Gibbs抽样FCDC是根据存在的数据通过统计方法得到的，由于Gibbs抽样本身所具有的良好性质，保证了所填充数据符合已存在数据的统计特性，从统计意义上而言具有一定的意义。这是Gibbs抽样仿真与使用人工填写、全局常量以及各类均值填充缺失值的区别所在。

另外，运用Gibbs抽样填充缺失数据是十分简单易行的。只要掌握缺失数据的属性与其他属性之间的条件分布，就能够利用这些分布产生数据。所以当已知的完整数据的数据量足够大，能够根据这些完整数据统计得到完整的条件分布，就能够利用这样的条件分布产生符合实际需要的数据。

当然Gibbs抽样作为一种仿真方法，最大的局限性在于仿真的基础是完全建筑在为随机数理论和计算机数系上的，伪随机数理论的算法再好也不是真正随机的，而计算机数系不但有限而且不完备。因而在使用Gibbs抽样进行仿真时，需要注意这一点。

[1]Jiawei Han,Micheline Kamber.范明,孟小峰译.数据挖掘——概念与技术[M].北京:机械工业出版社，2007.

[2]Jerzy W.Grzymala-Busse,Ming Hu.A Comparison of Several Approachesto MissingAttribute Valuesin Data Mining[A]. Rough Sets and Current Trends in Computing[C].Berlin:Heidelberg,2001.

[3]Smith A F M,Roberts G O.Bayesian Computation via the Gibbs Sampler and Related Markov Chain Monte Carlo Methods[J]. Journal of the Royal statistical Society,1993,55.