A Support Vector Machine Based on Bayesian Criterion
YU Chuan-qiang(于传强),GUO Xiao-song(郭晓松),WANG Yu(王宇),WANG Zhen-ye(王振业)
(1.The Second Artillery Engineering College,Xi’an 710025,Shaanxi,China;2.The Second Artillery Weather Center,Beijing 100089,China)
Introduction
Monitor devices always detect system’s state parameters and compare them with their normal values to decide the system’s running state.As changes of some factors,such as system model deviation,noise,system’s reference input and the external environment etc.,the deference between the detected parameter and its normal value is usually not zero even in normal system[1].In order to reduce the effects of the uncertainty factors on the parameter’s deference,thresholds are often introduced to enhance the robustness of the monitor device[2-4].The selection of threshold is important because a big threshold can cause high missing report rate and a small threshold can cause high false report rate.
In practical applications,the threshold selection method most in use is that based on 3σ criterion[5],where σ is the standard deviation of the detected parameter,and the better method is that based on minimum error probability criterion[6].
There are two significant shortcomings for the practical application of the method based on minimum error probability.Firstly,the prior probability is not taken into account.Secondly,the losses caused by wrong decision are not considered.
Aiming at the above two shortcomings,a Bayesian threshold selection criterion based on minimum risk is used in a certain weapon system’s state decision process.Compared with other criterion in the classification problem,Bayesian criterion has two advantages:i.e.,it considers the system’s prior knowledge,and it takes the losses caused by wrong decision into account.This criterion greatly improves the effect in the system state decision[7].
The main drawback of Bayesian criterion for the state decision is that the system’s distribution density has to be known and it is usually found out cumbersomely.There is a basic principle in the statistical learning theory[8]:in a solution of a given problem,we should try to avoid putting a more general problem as its middle step.Compared with the solution of parameter probability density,the classification of system state according to the detected parameters is a more specific problem.Therefore,a better solution idea is to classify the parameters directly according to the training samples,which omits the solution of probability density.
Classification is one of the major applications of SVM which can classify the test samples after training.Thus,it can be directly used to classify the detected signals and to judge the system’s state[9].But,it does not consider the classified problem’s prior probability and occurrence probability,and is only interested in the magnitude of the problem’s actual value,strictly speaking,the inner product of the sample for seedless function or the inner product of the kernel function for seed function,its solution depends on the characteristics of the training samples.According to the Bayesian criterion,if the prior probability of the classified information can be added into support vector machine algorithm,the reliability of the classification results will be enhanced.Next,the main idea of SVM based on the Bayesian theory and the implementation process of the algorithm will be discussed.
1 SVM in Classification Problem
Suppose two types of one-dimensional data{x1,…,xn}∈X,{y1,…,yn}∈Y,and their locations in the one-dimensional coordinate are shown in Fig.1,where▽and○represent the different categories respectively,and obviously,this group of data is linearly inseparable.

Fig.1 A group of linearly inseparable data
To solve this problem with SVM,one method is through introducing slack variables,misjudged loss or penalty parameter to extend the distance between the non-separable points in the training samples and the decision hyper-plane,so that the problem becomes linearly separable;the other is to use the kernel function to map one-dimensional data to a high-dimensional space,which is equivalent to change the original decision hyper-plane into hyper-surface,so that the issues can be resolved.Similarly,the above two method can be combined to solve the nonlinear non-separable problem.
However,the decision function obtained by training SVM with this data group will inevitably lead to misclassification,because the training data used in SVM crosses,as shown in middle part of Fig.1.The decision function’s establishment entirely depends on the training samples,the decision results for this sample group may be optimal,SVM can make the right judgments for this data group,but it is difficult to ensure to make high reliability judgment for other new data,especially near the data crossover,the misclassification probability is higher.In fact,this is an inevitable problem in the classification method to use the samples to make judgment,the basic reason is that the complete samples of the problem can not be obtained;even if we can obtain the complete samples,it may not be able to classify completely,and we can only make the optimal decisions based on the existing samples.
2 SVM Based on Bayesian Criterion
In weapon systems,the data crossover phenomenon of the detected parameters is quite prominent because the working environment is quite poor and some factors,such as interference,are very strong,many data detected as failure results may be caused by the interference and other factors.Therefore,the classification reliability is in doubt if the support vector machine is only used to carry out judgment and decision or the decision is only made on the basis of the analysis results for the historical samples.The method with higher reliability is to make decision by considering not only the historical information of the existing samples,but also the current information.
SVM has the advantage in the use of existing samples,therefore,we just discuss how to add the current information into SVM.For convenience,we take the one-dimensional sample as an example.

notes the support vector,the decision function of SVM can be expressed as

For a set of samples,the classification result de-pends on s(x).If X1={1.5,2,3.1,4,5}in f(x)=1 and X2={4.4,5.2,6,7}in f(x)= -1,trained SVM with the samples and classified them then,we can obtain the classification region,as shown in Fig.2.In Fig.2,the vertical axis denotes the value of s(x),the horizontal axis the value of sample,□ the sample in X1,○ the sample in X2,and ▽ the value of s(x).The divide point is the intersection of line a and horizontal axis,L1denotes the positive region,L2the negative region.The falsely divided samples A and B are the first sample in the left and right of line a,respectively.
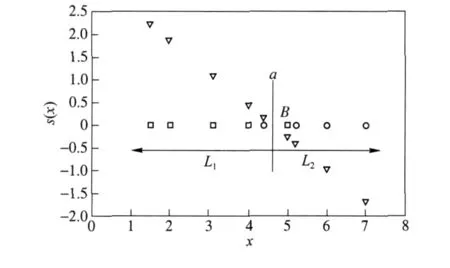
Fig.2 Classification region
This false divide issue is simply described in Section 1.In order to solve this problem,the slack variables,misjudgment loss(penalty parameter),kernel function or their combination will be introduced in SVM.
If such modified SVM can completely classify the training samples,a new problem will be engendered to use that classification method to solve practical problems.We can reasonably suppose that a test data is at point A belonging to positive type;when SVM classifies this data,it will be divided into negative type,because A in the training samples belong to negative type.The main reason causing the above phenomenon is that the area near points A and B belongs to the cross-region,the data at this area can not be classified accurately without other conditions.
Since we can not correctly classify,then we can only improve the accurate probability of the classification results as much as possible.A feasible solution on this issue is to add a prior probability to the decision function of SVM,i.e.,

Compared with the traditional decision function,c(p-0.5)is the added term,where c(-∞ <c≤∞)is the weighting coefficient,p(0 ≤p≤1)the prior probability,if p=0.5,there is no prior information of the samples.
The parameter p can be obtained from the prior probability algorithm or other ways.c depends on the sample characteristics.
2.1 Derivation of SVM Based on Bayesian Criterion
Following two rules can be summarized for the classification problem.
1)Point A belonging to positive-region can be classified as a negative type if the prior probability belonging to the negative type reaches a certain value,and vice versa.
2)For the point A belonging to the positive-region,the larger the value of s(A)is,the larger the prior probability to partition it into the negative type is,and vice versa.
We can obtain the algorithm to get the value of c according to the above simple rules.It can be discussed as the following three situations.
2.1.1 Falsely Divided Samples in Two Regions for Training Samples
1)The prior probability of the samples belonging to the positive type exceeds 0.5
For point B in Fig.2,if s(x)=s(B)<0,then f(B)=-1,and if c(p-0.5)≥ -s(B),then f(B)=1.Suppose that the value of s(x)is the smallest value in all falsely divided samples.It can be believed that point B is classified as positive type only if the prior probability of point B belonging to positive type reaches a certain value.In order to have higher reliability,the value of prior probability can be set to 1.Thus,we have

2)The prior probability of the samples belonging to the negative type exceeds 0.5
Similarly,for point A in Fig.2,we have

2.1.2 No Falsely Divided Samples in Two Regions for Training Samples
For convenience,we also take Fig.2 as an example.The points A and B are not the falsely divided points.In this case,the samples are completely separable,we can also use the similar calculation method.
1)The prior probability of the samples belonging to the positive type exceeds 0.5
For point B,suppose that s(x)is the smallest value in all negative samples,if s(x)=s(B)< 0,then f(B)= -1,and if c(p-0.5)≥ -s(B),then f(B)=1.Like the above method,it can also be believed that point B can be classified as positive type only if the prior probability of point B belonging to positive type reaches a certain value,therefore,we have

2)The prior probability of the samples belonging to the negative type exceeds 0.5
Similarly,for the point A in Fig.2,we have

2.1.3 Falsely Divided Samples in Only One Region for Training Samples
In this case,the problem can be solved by combining the above two methods.
2.2 Conclusions on SVM Based on Bayesian Criterion
Based on the above three cases, the value of c can be found out by using following two formulas.If p=0.5,the adding items in the formula(2)are zero,thus,c can be taken as any value.
1)If the prior probability of samples belonging to the positive type exceeds 0.5,

where the point B is the nearest point in the negative region to the demarcation line.
2)If the prior probability of samples belonging to the negative type exceeds 0.5,

where the point A is the nearest point in the positive region to the demarcation line.
Now,the problems for finding the value of the parameter c are solved.In this way,the problems for using the decision function of SVM based on Bayesian criterion to obtain the parameter values are all solved,and the implementation steps are as follows.
(1)Train SVM with the training samples;
(2)After training,test the training samples by using SVM;
(3)Find out the value of c according to the formulas(5)and(6);
(4)For a given sample,if its prior probability is known,substituting this value into formula(2)to get the classification result,and if it is unknown,substituting p=0.5 into formula(2)to get the classification result.
3 Problems in Application
In the above algorithm,the value of c only depends on the positive point or the negative point the nearest to the demarcation line,but it may not be reasonable in many cases.As we know,the support vector of SVM is the best point to reflect the characteristics of the classified sample.Therefore,the value of s(x)can be taken as the average value of s(x)of a few points near to the demarcation line.The experiment results show that the expansibility and robustness are improved by using such method.
In order to solute the prior probability,if the result of the testing data is negative type at a time,then the test data belongs to the negative type at the next time,and vise versa.Its probability can be taken as 1 in both cases,but different value of c represents different meanings.
In the status detection,the data of SVM inputs in a time sequence,the value of prior probability can be calculated according to the above method.For some static classification problems,such as the character recognition,image segmentation,and so on,the prior probability calculation needs to be further studied.
4 Verifications
For a temperature control device in a weapon system,its power is supplied by a regulated power supply with 28 V.The output power of this power supply is larger,and it is used very frequently and irregularly,thus,it is easy to be broken down.Now,we detect its status by using the common SVM and the SVM based on Bayesian criterion[10].
According to the system’s historical data,a training sample set including 200 normal date,with 27.6 in mean value and 0.55 in,standard deviation,and 200 data in exceptional status with 29.5 in mean value and 0.52 in standard deviation can be built.The distribution of training data is shown in Fig.3,where ○ denotes the sample in fault condition,* the sample in normal condition.It can be seen evidently form the figure that there is data crossover phenomenon in the two kinds of samples.

Fig.3 Distribution of training data
Now we train two kinds of SVM,a traditional SVM and a SVM based on Bayesian criterion with the samples.These two SVMs all use the support vector machine algorithm in type C,the value of parameter C is taken as 100,and use the RBF kernel function,the number of support vectors is 48 after training,which account for 12%of the entire samples.In the SVM based on Bayesian criterion,the number of positive support vectors is 23,and the value of parameter c is 1.177 5;the number of negative support vectors is 25,and the value of parameter c is -1.393 4.
After training,the actual detected data in sampling rate of 1 000 is classified by using two kinds of support vector machines algorithm.
4.1 Classification Results for Fault Data
The failure data is acquired when the filter capacitor in the power supply is burnt.The classification results are shown in Fig.4.

Fig.4 Classification results for fault data with two kinds of SVMs
The top curve in Fig.4 represents the measured output voltage of the power supply,which is changed from 100-th sample point,and reaches 29.1 in 110-th sample point.The above phenomenon is caused by the breakage of the filter capacitor in the power supply.The middle curve in Fig.4 shows the classification results of the traditional support vector machine algorithm.In this curve,“1”represents the normal status and“-1”the fault status.We find the fault in the 105-th sample point,and there is some false reported status during the fault.The bottom curve in Fig.4 shows the classification results of the support vector machine algorithm based on Bayesian criterion.Similarly,“1”denotes the normal status and“-1”the fault status,and the false reported status exists also,but the number of false report is reduced obviously.It shows the superiority of this algorithm.
4.2 Classification Results for Disturbed Data
We used the data,which is disturbed by the starting of a hydraulic system,to verify two support vector machine algorithms,as shown in Fig.5.The meaning of the curve in Fig.5 is similar to Fig.4.It can be seen from Fig.5 that the support vector machine algo-rithm based on Bayesian criterion has the better classification result.

Fig.5 Classification results for disturbed data with two kinds of SVM
5 Conclusions
The traditional SVM algorithm only uses the historical training sample and does not consider the current system status in the classification.The improved SVM algorithm based on Bayesian criterion overcomes the shortcoming of the traditional one.This new algorithm is used to detect the status of a weapon system,and the classification results show that it is better than the traditional algorithm.Both robustness and sensitivity of the algorithm are enhanced.
[1]LIU Chun-heng,ZHOU Dong-hua.An adaptive selection method for threshold in fault detection[J].Journal of Shanghai Maritime University,2001,22(3):46 - 50.(in Chinese)
[2]Ding X,Guo L,Frank P M.Parameterization of linear observers and its application to observer design[J].IEEE Transactions on Automatic Control,1994,39(8):1648-1652.
[3]Ding S X,Jeinsch T,Frank P M,Ding E L.A unified approach to the optimization of fault detection systems[J].International Journal of Adaptive Control and Signal Processing,2000,14(7):725 -745.
[4]Basseville M.Detecting changes in signals and systems[J].Automatic,1998,24(3):309-326.
[5]JIANG Yun-chun,QIU Jing,LIU Guan-jun,et al.A adaptive threshold method in fault detection[J].Journal of Astronautics,2006,27(1):36 -40.(in Chinese)
[6]FENG Shao-jun,YUAN Xin.A new method to identify the threshold in fault diagnosis[J].Journal of Data Acquisition and Processing,1999,14(1):30 - 32.(in Chinese)
[7]JIA Nai-guang.Statistical decision theory and Bayesian[M].Beijing:China Statistics Press,1998:78 -96.(in Chinese)
[8]Vapnik V N.The nature of statistical learning theory[M].New York:Springer-Verlag,2000:102-112.
[9]Granovsky B L,Hans-Georg Müller.Optimizing kernel methods:a unifying variational principle[J].International Statistical Review,1999,59(3):373-388.
[10]YU Chuan-qiang.The realization of fault diagnosis device in the temperature and electricity control and hydraulic system in XXX weapons system[D].Xi’an:Second Artillery Engineering Institute,2003.(in Chinese)
- Defence Technology的其它文章
- Experimental Investigation on Combustion Performance of Solid Propellant Subjected to Erosion of Particles with Different Concentrations
- A Real-time Monitoring System for Tire Blowout or Severe Leakage
- Research on Performance of U Separator in Sand and Dust Test System
- Prefix Subsection Matching Binary Algorithm in Passive RFID System
- An Orthogonal Wavelet Transform Fractionally Spaced Blind Equalization Algorithm Based on the Optimization of Genetic Algorithm
- An Evaluation Approach for Operational Effectiveness of Anti-radiation Weapon

