空气中电晕放电的Monte Carlo模拟
万 博,刘尚合,胡小峰,雷晓勇
(军械工程学院强电磁场环境模拟与防护技术国防科技重点实验室,石家庄 050003)
1 引 言
Monte Carlo法又称为随机模拟方法或统计试验方法[1-3],其基本思想是:首先建立一个概率模型或随机过程,使其参数等于问题的解;然后通过对模型或过程的观察、抽样来计算所求参数的统计特征。Monte Carlo方法以概率统计理论为基础,以随机抽样(随机变量的抽样)为手段,在很多方面有重要的应用。它的优点表现在3个方面:方法和程序的结构简单,易分析,易理解;收敛的概率性和收敛速度与问题的维数无关,很好地避免了维数问题;受问题条件限制的影响较小,大大提高了可行性。
随着科技的发展,人们的日常生活对电力能量的需求越来越大,高电压功率传输线被广泛应用在超高压、特高压电网中。与此同时,电晕放电在实际的高电压绝缘系统中非常重要。电晕放电是尖端带电体的电压达到一定值时,周围的气体发生局部电离和激发过程而形成放电通道,放电过程伴有微弱的辉光和声响,电极并不出现击穿或导通的现象。本文采用Monte Carlo法,用计算机仿真模拟电子和空气中分子的碰撞以及电子崩的形成,经过研究得到了电子崩的物理发展过程。
2 模型建立
2.1 电子在空气中运动
应用Monte Carlo法模拟电子在空气中运动,电晕放电[4,5]的物理模型相当复杂。在外部电场和空间电荷的作用下,本文用Monte Carlo法模拟了电子在空气中的运动,该模型应用统计的方法描述了粒子碰撞的过程,其中包括由光电离产生的电离子对。最初电子从阴极发射出来,它与空气分子是否发生碰撞是由一个随机变量R1所决定的,这个随机变量R1的取值均匀分布在0~1之间。如果P≥R1,那么假设碰撞发生在一个时间步长结束之后,此时P就是碰撞概率。如果 P 式中,v(ε)是电子的速度,QT(ε)是整个碰撞的横截面,N是气体密度,Δt是发射电子的间隔时间,ε是电子能量,Tm是碰撞时间。 在混合气体中,当电子与分子碰撞时,碰撞结果依赖于碰撞截面是否与碰撞类型相适应。为了确定碰撞的性质,将整个碰撞截面QT分解成所有可能发生的碰撞对应的截面,同时合理碰撞的极小概率值也被计算在内。 式中,P2,j是电子碰撞的极小概率值。 在0和1之间的随机变量R2决定了发生碰撞的类型。碰撞的类型由以下的条件决定: 式中,P2,j是碰撞发生的概率(弹性碰撞、电离碰撞),j=1,2,3,…,n。式(3)决定了第 j次的碰撞。在没有新粒子产生的条件下,电子损耗的能量与碰撞的类型相一致。在电离碰撞情况下,减去起始的能量,剩下的能量平均分配给两个电子。在碰撞结束后,在下一个时间步长中,粒子继续它的运动,以上过程重复进行。 应用Monte Carlo法模拟电晕放电在阴极点-平面的空气间隙内的发展过程。在阴极点到平面的空气间隙,电子和离子团的发展轨迹被模拟计算出来,其与大量的单个运动的电子相一致,如图1所示[7]。 图1 电极结构Fig.1 A diagram of the electrode geometry 假设电子崩的发生轨迹沿着间隙的中轴线运动,在此间隙中,电场变化很快。整个放电空间被分成两个区域,区域1靠近阴极点,空间电场强度很高,大多数的电子和离子都在此处;区域2就是除去区域1剩下的区域。本文把区域1分割成很多的小网格,电子的运动在这个区域被模拟出来,应用小的网格尺寸来改善模拟精度。与此同时,在区域1中,空间电荷的积累造成网格区域中电场的突变,其结果直接影响到邻近的网格内的情况,所以要用更小的网格尺寸Δz1。相比之下,在区域2中,相对大一点的网格尺寸Δ z2就足够了。 式中,M1和 M2分别是区域1和区域2的网格数量,d是间隙的长度,d1是区域1的长度,如果超过临界值,电子和离子将会使电场区域产生畸变。当所有的电子都已完成了运动模拟之后,电子的运动状态将被存储起来,继而利用其进行下一个时间步长内的计算。在这个间隙内,电子总和很大,所以很有必要去缩放比例,以此限制模拟粒子的数量。当模拟的总粒子数过大,从而使计算量超过计算机内存时,就需要一个程序,输入数据,用这个引入的子程序来模拟一些与存在的模拟粒子团近似相等的新的粒子团,每一个新的粒子代表着实际中旧的粒子的数倍。子程序包含旧的粒子团的速度分布,所以新的粒子团在相空间与之前的集团相等。经过研究得出结论,Monte Carlo法的优点在于大量的参数无需考虑,在计算中是可忽略的因子。 尖端带电体的电压达到一定值时,周围的气体发生局部电离和激发过程而形成放电通道,放电过程伴有微弱的辉光和声响,电极并不出现击穿或导通的现象,发生电晕放电。电晕放电的结果是创造了不同的荷电载体(正离子、负离子、电子)。Monte Carlo法是一个现实可行的技术,用来模拟电子和空气中分子的碰撞,以及电子崩的形成,用此方法可模拟电子崩的发展过程。得到的结果是,在空气中点到平面的几何结构中负的电晕放电。计算是在充满氮气的空间中,极间电压为3 kV。间隙中轴线的任一点的电场分布可近似表示为 式中,r1、d、z和V0分别代表尖端半径、间隙长度、距离阴极点的长度和所承载的电压。点到平面之间的间隙被分成两个区域,这个间隙总长度为d=5×10-3m,r1=5×10-4m,d1=1×10-3m,M1=50,M2=100。在本文中选择时间步长为0.5×10-12s。 初试时间t=0 s时,能量为0.1 eV的电子从阴极释放出来,在外电场的驱动下,由阴极发出向阳极运动。在此过程中电子将经历电离碰撞,这将使这一个电子产生一个离子和另一个电子。因此,在这个向阳极运动的过程中,将有一个扩张的电子云团,此过程就是电子崩。但离子云团在电子崩运动的过程中几乎是稳定不变的,处在离电子云团后面较远的位置。为了保持这个雪崩的趋势,需有另一种方式来补充,即光电离,它是激发态原子发生跃迁辐射出的光子与中性原子相互作用从而引发新电离的过程。光电离的位置由光电离点的概率所决定,这个光电离点由计算机在每一步长的最后生成随机变量。 电场在电晕放电发展过程中起着决定性的作用,场强E在不同时间随着间隙的变化而变化,如表1所示。在表1中,横格为在不同的间隙长度(0.5~2.5 mm),每一定的距离设置一个场强测量点;纵格为时间坐标(0.3~2.5 ns)。由表1可知,这是空间电荷的电子崩云团。在阴极上,高电场的区域变小。另外,由于空间电荷的影响,阴极点到正离子之间的电场强度随着时间的推移不断变强。 表1 场强变化Table 1 The field distribution at various points in time 图2记录了持续电子崩的初始状态和之后的发展趋势。最初电子从阴极释放出来,雪崩主体的趋势朝向阳极,不断地加速直到0.5 ns。在雪崩的主体向阳极的移动过程中,激发的原子同时发生电离。因此,在雪崩的主体达到它的最大规模前,光子将要从激发态被发出,然后将回到基态。这些光子将朝向任意方向发射,然后将在距离原点不同的位置被吸收。在0.8 ns时,由光电离产生的第二轮雪崩将发生,在阴极强场区域,其增长的速度将比第一轮的雪崩更快,但是其将在不久后消散。由于光电离的效应,第二轮的雪崩在距离第一轮雪崩不同的位置处开始。就像第一轮雪崩的形成过程,所有接下来的雪崩一旦形成,都要发射光子。这些光子产生新的光电子,这些光电子将开始第三轮的雪崩甚至更多的轮次。随着时间的推移,场的畸变不断加剧。对于负电晕,靠近电极的正电荷使在阴极表面的增长,在远离阴极的电场区域场强降低到几乎为零。在朝向正在发生电离的方向,电场有一个急剧的变化。在阴极点附近,随着电荷密度的增大,空间电荷对这个区域电场的影响在降低。图中第三轮雪崩的发生在1.0 ns,其电场强度明显高于前两次,而且电场是成倍地增长,比之前的雪崩更加剧烈,但与之前的雪崩发生规律相似。 图2 不同时间电子密度的分布Fig.2 Electron density distributions at various times 另外,由图2可知持续雪崩的发展状况,电子和离子密度以指数增长。从图中可得出结论:电子和正离子各自密度的峰值位置几乎不变。在阴极和空间电荷之间的区域中,增强电离的结果使空间电荷场有了变化,导致电子和离子密度的峰值发生了迁移,所以空间电场才朝向阴极运动。当电子在弱场区域,最终它将与分子相接触,然后减少。在靠近阴极附近仅存在一个强场区域,通常称为阴极强场区域。每一次新的电晕脉冲都需要有电子的注入。正离子分布的峰值朝向阴极移动,因为在稍后的电离阶段只能在强场区域。负离子分布和正离子分布有相似点,就是都有一个微小的峰值。 本文用Monte Carlo法模拟了空气中的负电晕放电。在空间的局部场,计算得到了电荷密度变化和电离的速度用来描述电晕放电的动力学性能。研究了雪崩的建立和持续发展过程,证实了空间电荷和光电离在电晕放电过程中起着重要作用,结果显示由阳离子团产生的空间电荷曾强了阴极和阳离子团之间的电场强度,使该区域的放电更加稳定。同时,空间电荷减弱了正离子团和阳极之间的电场强度,从而限制了电晕向阳极的扩展。 [1]李源慧.激光水下目标探测的Monte Carlo模拟[D].成都:西南交通大学,2009:19-21.LI Yuan-hui.The technology of underwater laser target detection base on Monte Carlo simulation[D].Chengdu:Southwest Jiaotong University,2009:19-21.(in Chinese) [2]王坤.Monte Carlo方法及其简单应用[J].高校理科研究,2010,10(2):513-514.WANG Kun.Monte Carlo Method and uncomplicated application[J].Science Research of University,2010,10(2):513-514.(in Chinese) [3]张亮,赵娜.基于BP神经网络Monte Carlo法的结构可靠性分析[J].现代电子技术,2010,323(12):59-61.ZHANG Liang,ZHAO Na.Structure Reliability Analysis Based onBP Neural NetworkMonte Carlo Method[J].Modern Electron Technology,2010,323(12):59-61.(in Chinese) [4]刘尚合.静电理论与防护[M].北京:兵器工业出版社,1999:180-184.LIU Shang-he.Static Electricity Theory and Protection[J].Beijing:Weapon Industry Press,1999:180-184.(in Chinese) [5]李尔宁,刘延冰,沈悦.电晕放电若干特性的探讨[J].高电压器,1998,6(2):16-21.LI Er-ning,LIU Yan-bing,SHEN Yue.The Discussion of some corona dischargecharacteristics[J].High Voltage Apparatus,1998,6(2):16-21.(in Chinese) [7]Jianfen Liu,GovindaG Raju.Simulation of Corona Discharge Negative Corona in SFG[J].IEEE Transactions on Dielectrics and Electrical Insulation,1994,45(3):520-529.
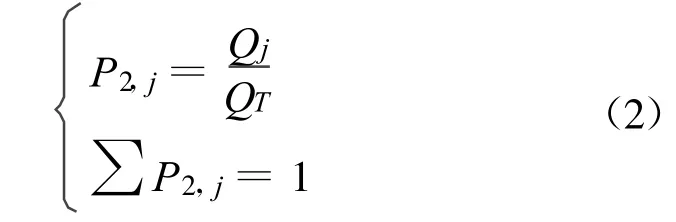

2.2 电晕放电在电极结构内的发展过程


3 结果和讨论



4 结 论

