基于FLUENT的插齿机主轴液压轴承静态特性研究
王 磊 田启华 张云才 杜义贤
(1.三峡大学机械与材料学院,湖北宜昌 443002;2.三峡大学电气与新能源学院,湖北宜昌 443002)
静压支承由于具有良好的润滑和承载性能而逐渐受到关注,尤其在高精度、重载荷机床中的应用越来越广泛[1].为了解决插齿机高速运行时的摩擦和温升问题,高速插齿机的主轴支承广泛采用液体静压轴承.然而,由于插齿机主轴工作时运动较为复杂,既有轴向的直线往复运动,又有周向的旋转运动,因此,主轴液体静压轴承的流体运动也很复杂,很难通过实验或理论的方法得到比较精确的结果,比如轴承的压力分布,速度矢量等结果.现阶段,关于静压轴承的数值仿真主要集中在气体静压轴承方面,其计算方法通常是在一系列的假设条件下对雷诺方程进行二维简化,由于有限差分法和有限元法发展时间较早,经过几十年的发展,其理论已相对成熟,在进行静压轴承的数值仿真时研究者都习惯采用理论相对成熟的有限差分法[2-4]和有限元法[5-6]等数值分析法对简化的雷诺方程进行计算.而采用有限体积法对液体静压轴承流场进行数值仿真的则相对较少.
在采用有限差分法时,差分方程只能认为是对微分方程的数学近似,基本上没有反映其物理特征,计算结果可能表现出某种不合理现象[7].而有限元法虽然在固体力学方程的数值计算方面取得了巨大的成功,但是由于有限元离散方程也只是对微分方程的数学近似,当处理流体流动和传热问题的守恒性、强对流、不可压缩条件等方面的要求时,有限元离散方程中各项还无法给出合理的物理解释,对计算出现的一些误差也无法改进,因此,有限元方法在流体力学和传热学中的应用还存在一些问题[8].但采用有限体积法时,用有限体积法导出的离散方程可以保证其具有守恒特性,而且离散方程系数物理意义明确,计算量相对较小,计算效率高,可以使研究者从繁琐的雷诺方程的编程求解中解脱出来[7].因此,本文应用基于有限体积法的计算流体动力学软件FLUENT,对插齿机主轴支承中用到的液体静压径向轴承内部的流体进行数值计算,通过FLUENT软件的后处理功能计算出轴承的承载能力、刚度、流量等结果.并通过对主轴在静态和旋转运动状态下轴承的流场进行三维数值仿真,分析并得出轴承径向间隙、主轴偏心率、主轴旋转速度等因素对轴承承载能力和油膜刚度的影响规律,为插齿机主轴静压轴承的设计和优化提供新的计算方法和参考依据.
1 液体静压轴承的分析模型及求解流程
1.1 静压轴承的分析模型
研究主要针对插齿机主轴液体静压轴承的流体区域,在不影响分析结果的前提下,为了在数值仿真时建模的方便,可以对模型进行适当的简化.因此,在建模时忽略了轴承的一些倒角结构.轴承结构如图1所示.
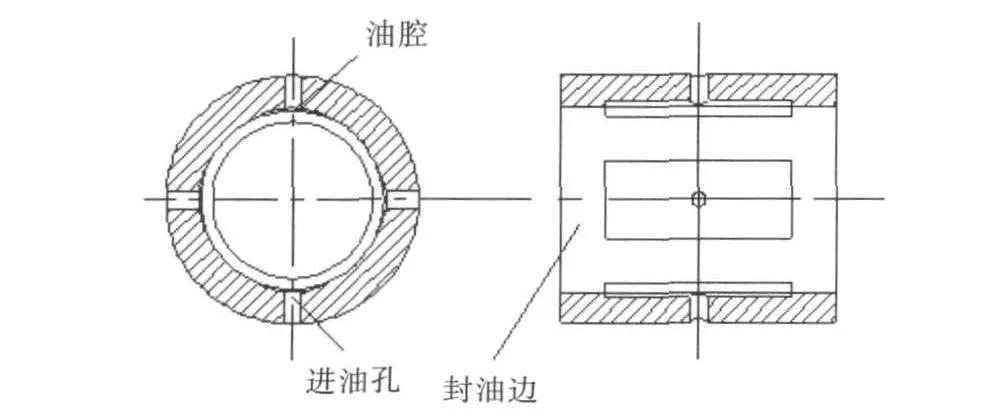
图1 静压轴承结构图
此轴承采用径向结构,周向均匀分布四对称油腔,无周向回油槽,主轴直径为85mm,轴承的长径比L/D=1.3,取轴承油腔长度L=110mm,每个油腔都有4个进油小孔,小孔直径d=3mm,轴向封油边长度为8 mm,设计间隙即油膜厚度为30μ m,油腔周向包角φ=54°,在设计状态下主轴偏心率ε=0.2,润滑油的动力粘度μ50°=0.021Pa◦s,润滑油的密度ρ= 900kg/m3.供油系统采用恒压式,液压油泵供油压力Ps=3MPa.
因为此模型的求解是基于有限体积法的计算流体力学分析软件FLUNET,采用FLUNET进行求解时,大体流程如下[9]:首先在FLUNET前处理软件Gambit中创建轴承流场区域的模型,并采用结构化的网格划分方法对模型划分网格,指定边界条件;接着将生成的网格文件导入FLUENT中,检查网格质量、修改模型尺寸单位、设定流体模型和边界条件,选择求解器和求解算法、设定松弛系数、进行流场初始化并指定迭代步数后开始求解计算;最后通过FLUNET后处理功能输出相关求解结果.
由上述的轴承结构参数在FLUENT前处理软件Gambit中建立轴承流场模型如图2所示.

图2 静压轴承流场三维模型
1.2 网格划分
网格划分同样在Gambit中进行,因为此模型尺寸变化比较大,而且模型总体尺寸也比较大,如果全部按照模型最小尺寸均匀划分,则会划分出很大数量的网格,会占用很大的计算机内存,对以后的模型计算不利.因此需要采取非均匀网格划分,对模型比较厚的区域(油腔处)进行粗划分,而对模型比较薄的区域细划分,但是模型油腔处线条直接与需要细划分的部位相联,中间缺少过渡,因此需要对油腔处的边线进行打断处理,然后再对边线进行非均匀网格划分,将打断边线的中间部分采用线节点粗划分,油膜薄壁处边线节点细划分,16个进油入孔处粗划分,并对进油小孔和油腔相接触的地方采用边界层的过渡处理方法,进行线节点的三级划分,最后对整个模型采用四面体网格单元划分.共得到 377 210个节点、1190002个单元,网格划分成功后,进行边界条件类型的指定,在此模型中,16个进油小孔的上表面设置为压力入口边界类型,油膜薄壁的两个端面设置成压力出口边界类型,其余的表面默认为wall类型.划分完成后进油小孔附近的网格局部放大如图3所示.

图3 静压轴承流场网格局部放大图
1.3 设定边界条件
将上面产生的网格文件导入FLUENT中进行求解,通过检查,网格质量良好,然后修改模型尺寸单位为mm.轴瓦与轴间隙中油膜的运动,实际是粘性流体动力学问题.由于油膜的实际流动情况比较复杂,想通过仿真得到精确的结果比较困难;而本文主要进行主轴静态特性的数值仿真,主要考虑轴承的静压效应.因此可以将轴承流场的分析简化为稳态分析,又通过计算得到轴承中流体的雷诺数很低,处在层流的范围内.故本文的仿真是在牛顿流体、不可压缩、层流和定常的条件下进行.接着设置润滑油的材料参数,选择相应的求解器,然后设置在网格文件中已经指定的边界条件类型,施加的边界条件如下:(1)所有入口压力处的压力均为油泵输出压力,即Pi= Ps=3MPa;(2)两个出口压力处的压力为大气压力; (3)液体流场和主轴相接触的内壁面及与轴承相接触的外壁面的速度均为零;(4)轴承内流体的流动为绝热过程,即流体的温度不变.
边界条件设定完毕之后,选择压强速度耦合求解的SIMPLE算法作为控制方程的求解算法,然后合理设定松弛因子以便有效地控制收敛速度及精度,最后初始化流场并设置迭代步数开始迭代求解流场的控制方程.
1.4 分析计算结果
压力场的分布图对研究静压轴承的承载情况有重要的参考意义.为了求解静压轴承对主轴的承载情况,必须先求出静压轴承中流场的压力分布,即静压轴承流体的压力场.因此输出轴承的压力场等值线图如图4所示;图中不同的颜色代表压力大小的不同,从红色到蓝色,压力逐渐减小,红色的区域压力最大,蓝色的区域压力最小,为了更清楚地研究轴承的压力分布及承载情况,输出流场与主轴相接触的内壁面的压力场分布如图5所示;速度场是对液体流动状态进行的模拟,它显示流体在一定条件下,流体的不同速度分布情况.同压力场等值线图类似,速度场图中的不同颜色代表油膜中流体的不同流动速度,从红色到蓝色,流体的速度逐渐减小,红色的区域流速最大,蓝色的区域流速最小.它还可以通过速度梯度的方式来直观地显示流场各处流体速度的变化趋势.通过对该模型的迭代计算得到的速度矢量图如图6所示.




2 相关因素对轴承静态特性的影响
2.1 偏心率及主轴间隙对承载能力及轴承刚度的影响
偏心率ε是液体静压轴承设计中的一个重要参数,它是主轴在受到外在载荷时的径向偏移量和轴承的初始设计间隙之比,0≤ε≤1,在主轴受到外载时,ε不可能为零,只能无限接近于零,它也不能为1,否则主轴将直接与轴瓦接触,产生剧烈摩擦.偏心率对轴承的静态特性有着重要的影响,在设计过程中应该根据加工精度以及主轴受力情况综合选择.
为研究偏心率对轴承静态特性的影响,在轴承其它参数不变,供油压力Ps=3MPa,油膜厚度分别为30μ m,40 μ m、50 μ m、60 μ m,偏心率ε分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9的参数下进行了数值仿真,并对仿真结果拟合成曲线,如图7和8所示.
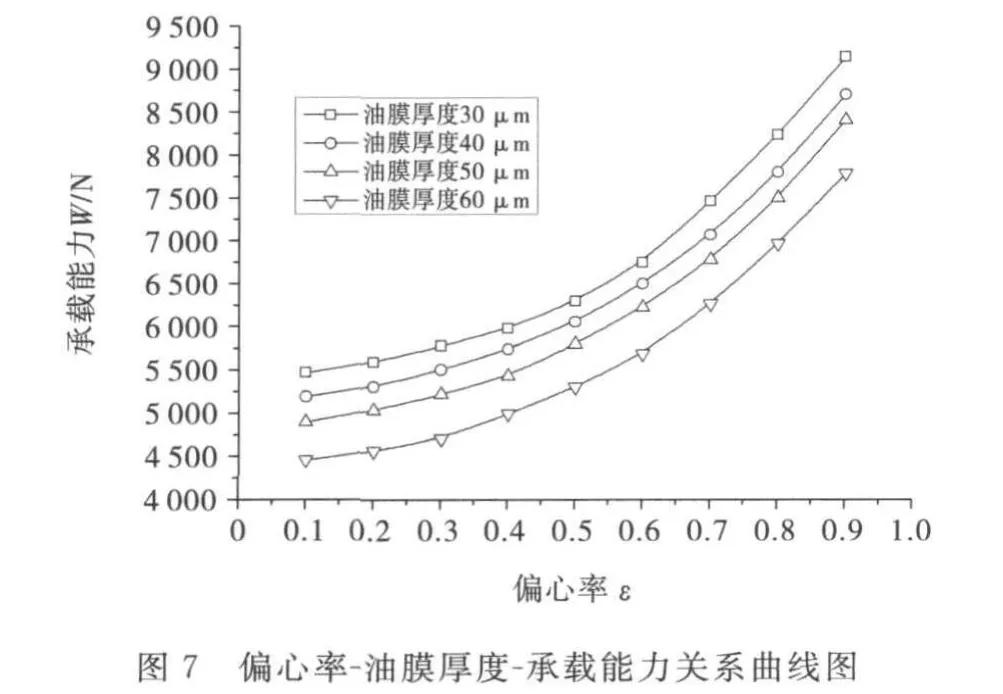
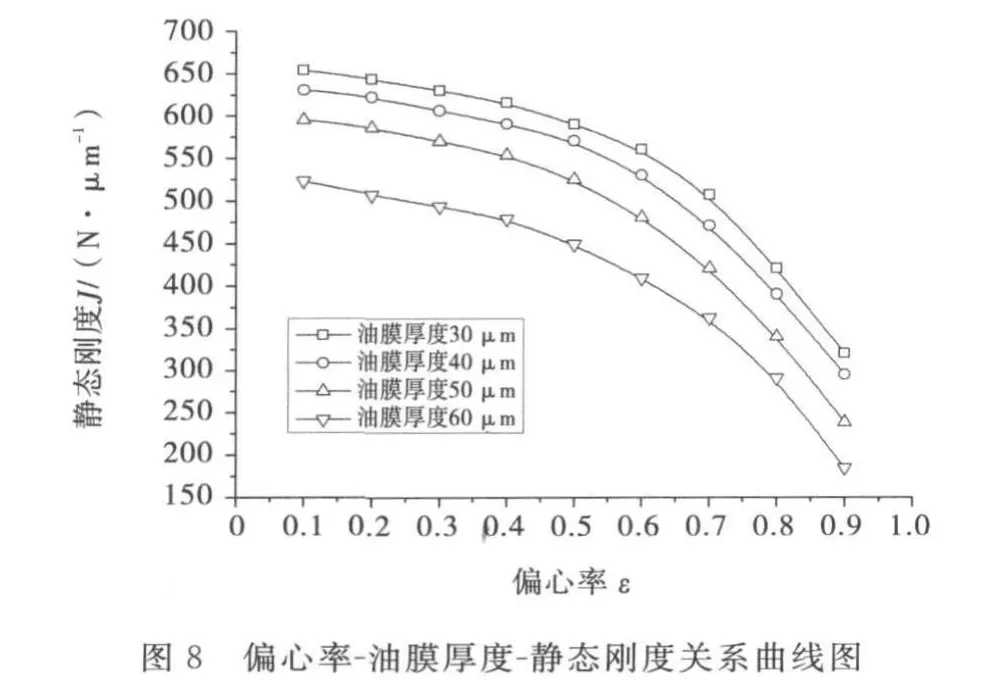
从图7~8可以看出:在同一油膜厚度下,随着偏心率的增大,轴承的承载能力逐渐增大,并且增长的速度越来越快,轴承的静态刚度却在逐渐减小,并且减小的速度越来越快;而在同一偏心率下,随着油膜厚度的增大,轴承的承载能力和静态刚度都在逐渐减小,并且减小的速度越来越快.所以在同一偏心率下,轴承的静态刚度和承载能力不能兼顾,只能根据设计需要选取适当的偏心率.油膜厚度即主轴间隙的增大对轴承的静态特性是不利的,并且还会增大供油泵的流量和轴承的摩擦功率,为了得到静压轴承良好的静态特性,理论上主轴间隙越小越好,但是由于加工工艺及加工精度的限制,主轴间隙也不可以无限小,只能在加工工艺和精度允许的条件下选取合适的值.
2.2 主轴转速对承载能力及油膜刚度的影响
主轴转速是插齿机运动的重要参数,它由插齿机的加工工况决定.在轴承其它结构参数不变,主轴间隙为30μ m,供油压力Ps=3 MPa,偏心率ε分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9,主轴转速分别为1000 r/min、3000 r/min、5000r/min、7 000 r/ min的参数下进行了数值仿真,并对仿真结果拟合成曲线,如图9~10所示.
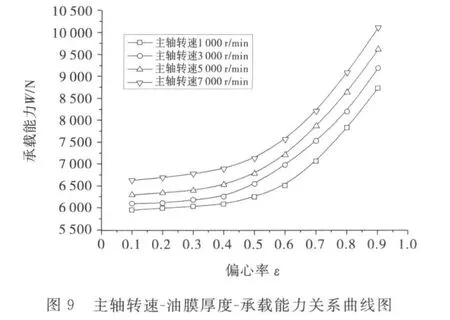
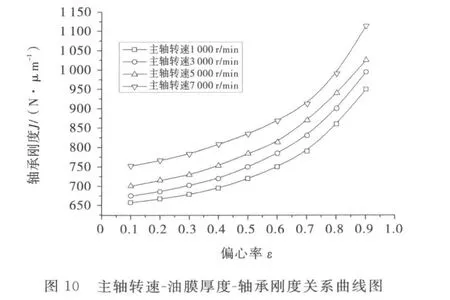
从图9~10可以看出:在同一偏心率下,轴承的承载能力和刚度随着主轴转速的增大而增大,并在设计范围内时,主轴转速越高,轴承的承载能力和刚度越大;而在同一转速下,在小偏心率(0<ε≤0.4)时,轴承的承载能力和轴承刚度变化很小,而在大偏心率(0.4<ε≤0.9)时,轴承的承载能力和轴承刚度却随着偏心率的增大而增大,并且增大的速度越来越快.这是因为在小偏心率和低转速时,轴承主要表现的是静压效应,而在在大偏心率和高转速时,轴承存在动压效应,并且不能忽略.
3 结 语
通过基于有限体积法的计算流体力学软件FLUENT对插齿机主轴静压轴承流场的三维数值仿真,计算了轴承的承载能力,轴承刚度,并分析了主轴偏心率、主轴间隙、主轴转速对承载能力和刚度的影响,得出了如下结论:
(1)主轴间隙的增大对轴承的承载能力和刚度有不利影响,为了得到较大的承载能力和刚度,应在加工工艺和精度允许的条件下选择小的主轴间隙.
(2)轴承在静态工作时,在同一主轴间隙和供油压力下,随着偏心率的增大,轴承的承载能力逐渐增大,并且增大的速度越来越快,而轴承的刚度却在逐渐减小,并且减小的速度越来越快.
(3)在主轴有旋转运动时,随着转速的增大,轴承的承载能力和刚度均增大,在小偏心率低转速时,轴承的承载能力的刚度变化较小,主要表现为静压效应;在大偏心率高转速时,轴承的承载能力和刚度变化较大,此时,轴承存在动压效应并且不可忽略.
以上结论可以有效地指导插齿机主轴静压轴承的设计和优化,为插齿机静压轴承的设计和优化提供了新的计算方法和参考依据.但是由于时间仓促及笔者理论水平有限,暂时只考虑了单一因素对轴承静态特性的影响,多因素的情况没有做进一步的研究,它将是后续工作的重点,在后续的工作中会对此进行更深入的探索与研究.
[1] 张国良.从静压轴承看静压技术的应用[C].求新科协科技论文集,1997(1):118-121.
[2] Lo Chengying,Wang Chengchi,LeeYu-Han.Performance Analysis of High-speed Spindle Aerostatic Bearings [J].Tribology International,2005,38:5-14.
[3] 章正传.小孔节流静压气浮轴承-转子系统动力学特性研究[D].哈尔滨:哈尔滨工业大学,2006.
[4] Belforte G,Zaidi H,Frene J,et al.Theoretical Investigation of Fluid Inertia Effects and Stability of Self-Acting Gas Journal Bearings[J].ASME,1999,121(10): 836-843.
[5] 李锻能,张恩龙,马 平.应用Marc分析气体静压轴承静态性能[J].润滑与密封,2005(5):47-79.
[6] 彭万欢.静压气体径向轴承的静动特性研究[D].北京:中国工程物理研究院,2006.
[7] 饶河清.基于FLUENT软件的多孔质静压轴承的仿真与实验研究[D].哈尔滨:哈尔滨工业大学,2006.
[8] 李人宪.有限体积法基础[M].北京:国防工业出版社, 2005.
[9] 王瑞金,张 凯,王 刚.FLUENT技术基础及应用实例[M].北京:清华大学出版社,2007.

