纤维金属混杂层合板拉伸强度分析
姜舜,赵耀
(华中科技大学船舶与海洋工程学院,湖北武汉 430074)
0 引言
纤维金属混杂层合板(Hybrid fibre-metal laminates,FML)是由纤维增强树脂层与金属薄层交替粘接而成的1种新型结构材料,如图1所示。其既具有传统玻璃钢的轻质、高强度、优越的抗疲劳和耐环境的性能[1-3],同时相比于相应的单一轻金属合金更耐疲劳。其优点是能像常规金属合金薄板那样进行处理和加工[4-8],同时具备玻璃纤维和轻金属的材料特性。FML中纤维层的各向异性特性为结构的可设计性创造了条件,即通过改变层合板各单层的纤维方向,铺层顺序,金属层厚度来满足结构强度和刚度的方向性要求,因此,在船舶制造及海洋工程和航空领域得到了越来越广泛的应用。
考虑到纤维金属混杂层合板在船舶建造领域的应用,以及其在大型复杂船舶结构有限元分析的可靠性问题。本文在层合板理论方法的基础上,对纤维金属混杂层合板的解析解进行扩展,使其能适用于纤维金属混杂层合板,并利用有限元对纤维金属混杂非对称层合板进行数值分析,并与单向拉伸条件下的试验值比较,认为有限元计算能满足工程计算的要求;同时,讨论了铺层方式、金属层厚度以及金属层材料属性对拉伸强度的影响,为大型复杂结构的有限元分析提供有益的参考。
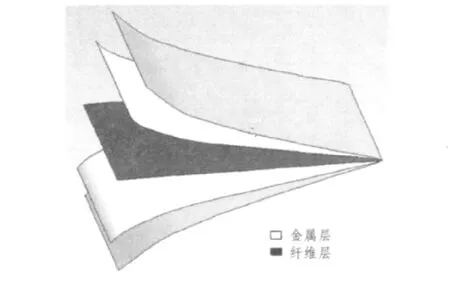
图1 纤维金属层合板FMLFig.1Hybrid fibre-metal laminates
1 层合板理论解的扩展
由于纤维金属混杂层合板中金属层的存在,金属弹塑性应力-应变关系与玻璃纤维的本构关系的差异,需要对经典层合板理论进行扩展以适用于FML。同时,基于非对称层合形式,根据计算层合板非中面刚度系数的方法进一步扩展层合板理论得到非对称层合板刚度系数。
1.1 含金属的层合板刚度矩阵
基于弹性力学薄板理论来讨论层合板的应力和应变关系,即层合板的刚度。首先,对于一般正交各向异性层合板面内载荷作用在材料主应力方向,得到不考虑温度因素影响时的一般层合板的广义力和广义应变关系[1],即:

式中:N和M分别为层合板的单位长度的内力和内力矩;ε0和κ为中面应变和中面扭曲率;A,B,D分别称为面内刚度矩阵、耦合刚度矩阵和弯曲刚度矩阵。当考虑有金属层的存在,展开形式增加了金属层刚度矩阵,即:
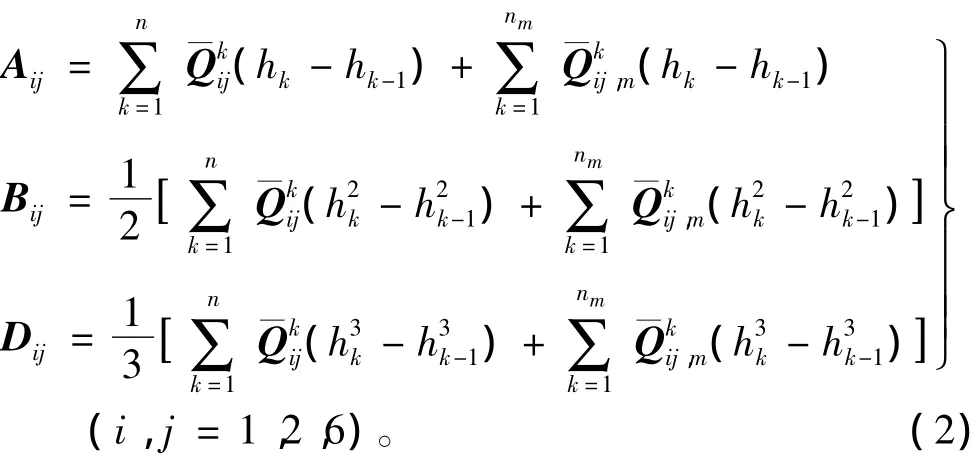
式中:hk和hk-1为第k层上下表面的z坐标值,如图2所示;Qij,m为金属层的刚度矩阵。
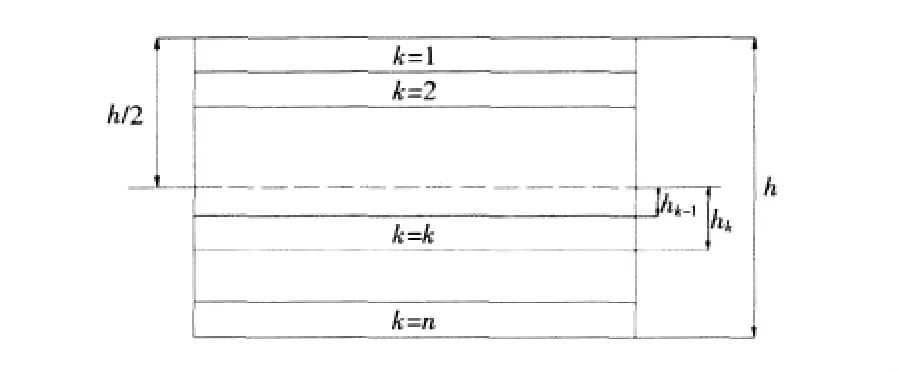
图2 具有n个单层的层合板Fig.2Laminates with n layers
当金属层扩展到层合板理论后,在分析FML时,金属层的弹塑性关系也需要考虑。金属层具有双线性特征的应力-应变关系[8],并且金属的屈服遵守VonMises屈服准则,当金属层等效应力达到屈服强度σy后,金属层的总应力值和总应变值都可表示为:
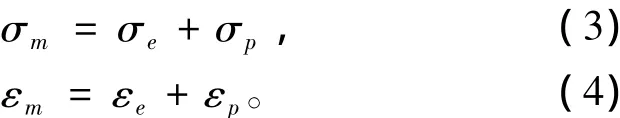
1.2 非对称层合板的刚度矩阵
以上讨论层合板刚度时,都将参考坐标系原点取在层合板厚度方向的几何中心上,得到的是中面刚度系数。但是实际的工程结构往往采用的是不对称的层合板铺设形式,因此,本文又进一步对经典层合板进行扩展,利用计算非中面刚度系数,将每一层板看成偏离层合板中面的特殊层合板,此时层合板非中面刚度系数矩阵可表示为:

式中,d为假设面板中面到参考坐标轴的距离。
2 有限元与理论解结果对比
本文使用通用有限元结构分析系统对纤维金属混杂非对称层合板在承受单向受拉的情况下进行数值分析,验证扩展的层合板理论解正确性。选取具有4个节点且每个节点有6个自由度的SHELL181单元[9]来模拟,铺层形式为[Al/0/-45/45/90],Al即金属铝层厚度为0.5 mm,其余各FRP层厚度为0.125 mm。其中,Al层为铝合金材料,E=72 GPa,ν=0.33,FRP层为碳纤维增强复合材料,其单层属性如表1所示。

以面内载荷100 N/mm作用在尺寸为25 mm× 100 mm的几何模型上,网格划分、约束条件、受力状况如图3所示。
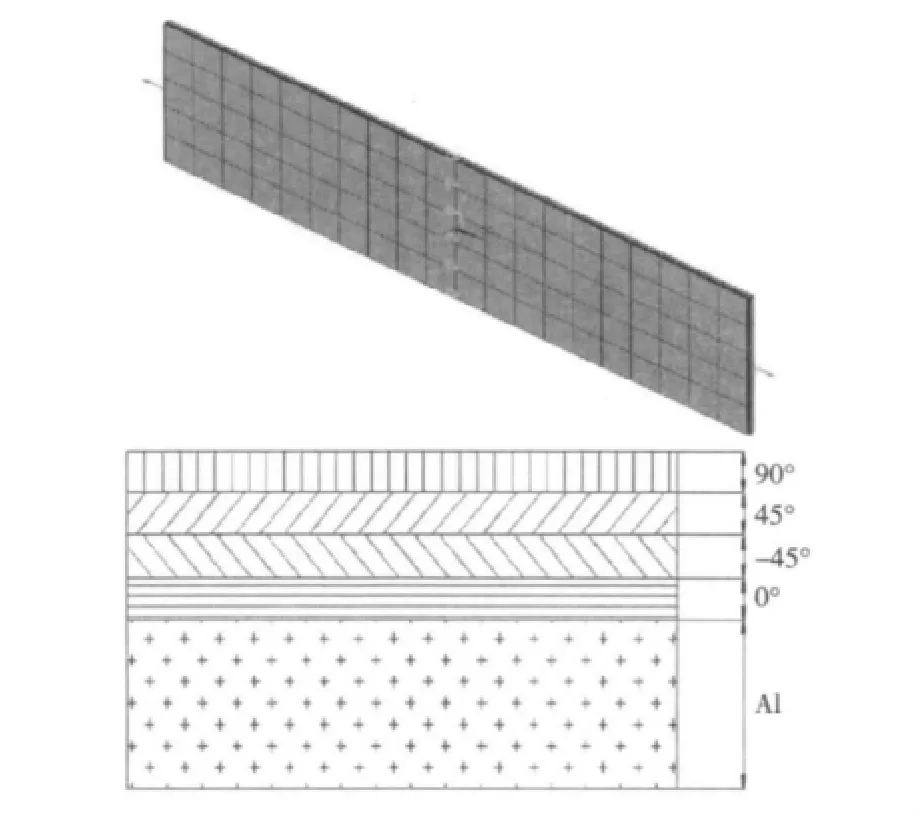
图3 有限元计算模型Fig.3The finite element model
通过扩展的层合板理论解和数值计算结果列于表2,经过对比可以发现,数值计算得到的各层应力值和理论解相符。图4和图5分别显示了数值计算中X和Y方向的应力计算在不同层内的分布情况。

由图4可知,由于FML板为非对称层合板,在载荷作用下,板发生了翘曲变形。分析变形产生的原因是:混杂层合板各层的材料属性各异,承受同一拉载荷时应力和应变关系不一致,导致一侧变形较另一侧变形大最终反映在整体结构上就产生了翘曲变形形式。研究纤维金属混杂层合板的变形特性,有助于掌握变形规律,从而实现对变形的控制和利用,以得到特殊工艺曲面,应用于工程实践。
图5表示FML板X方向应力在厚度的分布情况,由于纤维不同方向的弹性模量随铺设角度的变化而不同,因此应力在受拉的条件下的响应也不同。X方向最大应力位置都出现在FML的中心并向两端递减。经过2种方法所得结果的比较可以发现,扩展的理论解与有限元数值计算结果吻合得相当好,证明了有限元数值计算在描述纤维金属混杂层合板拉伸特性方面具有相当的可靠性,使其成为计算大型复杂结构的重要依据。

图5 FML板X方向应力值分布Fig.5The stress in X direction
3 计算实例分析
3.1 FML单向拉伸试验的数值模拟
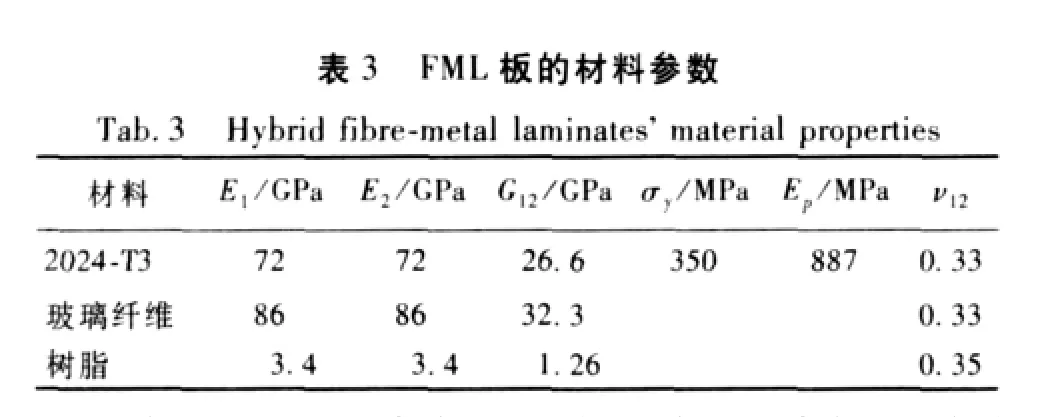
数值计算和理论值的比较取得了很好的吻合结果,通过数值模拟FML拉伸试验进一步验证扩展层合板的理论正确性,选取文献[10]中的混杂层合板结构。为真实模拟试验,完全依据文献提供的构件尺寸,计算模型的铺层顺序为[Al/0/90/90/0/Al],FRP层厚度为0.146 mm,Al层厚度为0.489 mm,板尺寸为305 mm×25.5 mm,FML板材料参数如表3所示。
运用通用有限元结构分析系统得到模拟试验的拉伸应力-应变曲线如图6所示,根据有限元计算绘制的应力-应变关系与试验结果的对比可以发现:在单轴拉伸载荷作用下,FML层合板拉伸强度表现出双线性关系。在初始线性阶段,Al层和FRP层共同承载外力载荷。当应力达到267 MPa时,Al层达到屈服应力,Al层承载能力逐渐下降,此时应力-应变曲线即开始偏离原线性路径,应力进行了重新分布,这时载荷主要由FRP层承载。可以发现,在相当长的加载过程中,数值计算结果和试验值吻合得非常好,只有在加载的后端由于FRP层随着载荷的增加逐层失效,计算结果与试验值出现分离,这一现象也与选择的壳单元有关,并没有考虑层间应力在抗拉强度时的作用。

图6 模拟拉伸试验的应力-应变曲线Fig.6Stress-strain curves of FML under uniaxial tensile loading longitudinal
3.1.1 铺层方式对拉伸强度的影响
为研究铺层方式对纤维金属混杂层合板拉伸应力-应变的影响,数值计算了θ分别为0°,15°,30°,45°,60°,75°和90°时的尺寸为300 mm×30 mm板拉伸应力-应变的关系。铺层方式为[Al/θ/θ/Al/θ/θ/Al],FRP厚度0.15 mm,Al层单层厚度0.5 mm,材料参数参照文献[10],加载方式均采用应力加载方式,计算结果如图7所示。
由图7可见,随着角度的变化弹性阶段的曲线趋于一致,只有在达到屈服点的位置有所差异。塑性部分的变化在0°~45°范围内是随着角度的增加而曲线的斜率逐渐降低,45°~90°范围内角度的增加曲线变化范围很小。曲线的趋势在45°前后产生截然不同的特性,分析此现象出现的原因是在小角度范围FML主要由刚度较大的FRP层承载,而在大角度范围初始阶段Al层和FRP层刚度相近,共同承受载荷因此应力很快达到屈服应力,应力也在Al层进入塑性后重新分布,导致刚度下降较快。

图7 不同铺层方式的应力-应变关系Fig.7Stress-strain curves in different angle ply
3.1.2 正交铺层方式对拉伸强度的影响
为了讨论正交铺层方式对纤维金属混杂层合板拉伸应力-应变的影响,本文选取了3组纤维层相互垂直铺设[Al/0/90/Al/90/0/Al],[Al/30/-60/Al/-60/0/Al],[Al/45/-45/Al/-45/45/Al]时板拉伸应力-应变的关系,计算结果如图8所示。
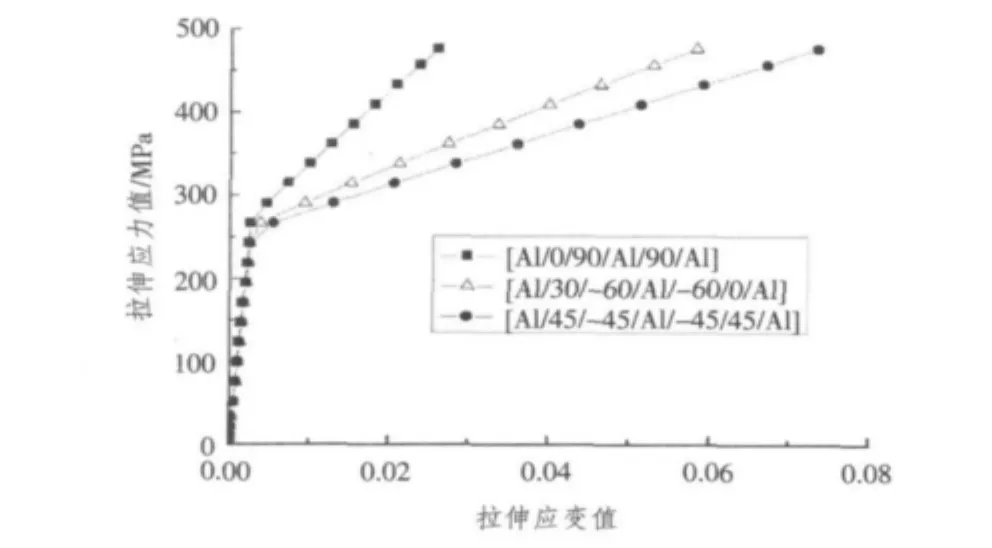
图8 不同正交铺层方式的应力-应变关系Fig.8Stress-strain curves in different orthogonal ply
分析计算结果,FRP层都是采用相互正交的铺层方式,虽然在屈服点位置上非常接近,然而继续加载后,随着正交角度的改变,载荷方向的抗拉模量也随之规律变化,不同的正交角度产生了不同的应力-应变特征,[Al/45/-45/Al/-45/45/Al]铺层方式的FML在金属层进入塑性段后刚度下降最快,而[Al/ 0/90/Al/90/0/Al]方式下刚度下降最慢。
3.1.3 金属厚度对层合结构的影响
为了研究金属层厚度对纤维金属混杂层合板拉伸应力-应变的影响,分别数值计算了Al层厚度为0.2~0.5 mm的FML拉伸应力-应变关系。铺层方式为[Al/0/90/90/0/Al],计算结果如图9所示。

图9 不同厚度的应力-应变关系Fig.9Stress-strain curves in different thickness of metal
图9所示,随着Al层厚度的增加,屈服应力点成正比例增大。由此可见,金属层的厚度对FML的拉伸强度的影响是很大的,而且是成比例的增加。因此,可以通过增加金属层的厚度来提高纤维金属混杂层合板的整体拉伸强度。
3.1.4 金属层材料属性对层合结构的影响
考察不同金属材料属性对纤维金属混杂层合板拉伸应力-应变的影响,计算了金属层材料参数分别为Em=70 GPa,90 GPa,110 GPa和130 GPa时FML拉伸应力-应变的关系,铺层方式为[M/0/0/0/0/M],M代表金属层,其厚度为0.5 mm,计算结果如图10所示。
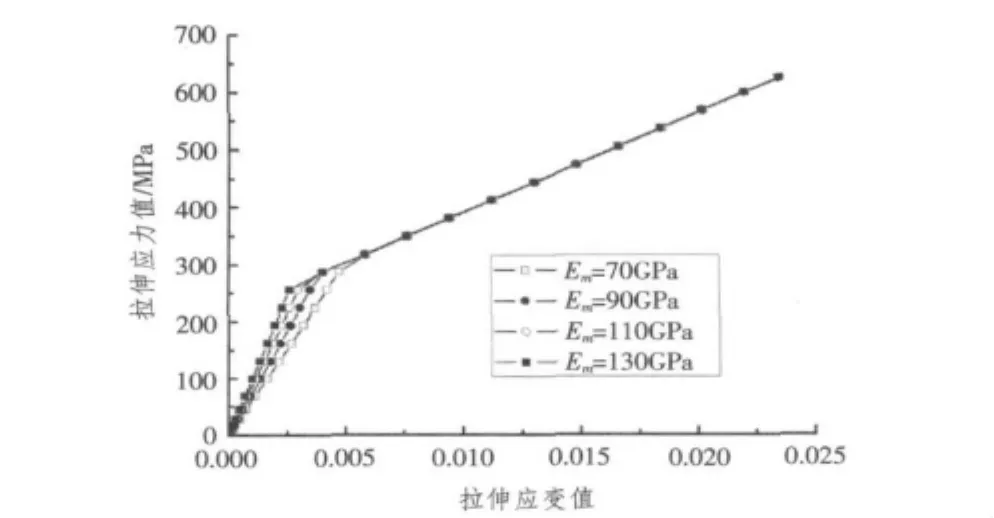
图10 不同金属材料的应力-应变关系Fig.10Stress-strain curves in different properties of metal
从图10中可以看到,由于金属层的弹性模量的增大,发生屈服应力值也随之增大,当FML的金属层进入塑性之后,层合板的应力-应变关系趋于一致,表现出相同的应力-应变特征。
4 结语
基于经典层合板理论,对纤维金属混杂非对称层合板的理论解进行了扩展,考虑了金属层的弹塑性特征对层合板拉伸特性的影响,经过与数值计算结果的比较,证明该扩展形式能较好地模拟纤维金属混杂非对称层合板特性。同时,进一步利用有限元计算和对称层合板拉伸试验结果很好的吻合,保证了纤维金属混杂层合板拉伸强度分析的正确性。
本文还讨论了铺层方式和金属层板厚对FML的影响,并且得到以下结论:
1)随着铺层角度的变化,FML拉伸弹性阶段的性质趋于一致,但是在达到屈服点的位置有所差异;塑性部分的变化在0°~45°范围内是随着角度的增加而曲线的斜率逐渐降低,45°~90°范围内角度的增加曲线变化范围很小。因此,不同的铺层方式对FML拉伸强度的影响是不同的。
2)不同的正交角度产生了不同的应力-应变特征,屈服点位置上非常接近,然而继续加载后[Al/45/-45/Al/-45/45/Al]铺层方式的FML在金属层进入塑性段后刚度下降最快,而[Al/0/90/Al/90/0/Al]方式时刚度下降较慢。
3)随着Al层厚度的增加,屈服应力成正比例增大。金属层的厚度对FML的拉伸强度的影响是很大的,而且是成比例的增加。
4)由于金属层的弹性模量的增大,发生屈服应力值也随之增大,当FML的金属层进入塑性之后,层合板的应力-应变关系表现出相同的特征。
[1]矫桂琼,贾普荣.复合材料力学[M].西安:西北工业大学出版社,2008.
[2]布赖恩,哈里斯.工程复合材料[M].陈祥宝,张宝艳,译.北京:化学工业出版社,2004.
[3]赵美英,陶梅贞.复合材料结构力学与结构设计[M].西安:西北工业大学出版社,2007.
[4]GUACAI W,YANG J M.The mechanical behavior of gLARE laminates for aircraft structures[J].JOM,2005,57:1-72.
[5]REYES G,CANTWELL W J.The mechanical properties of fibre-metallaminatesbasedonglassfibre-reinforced polypropylene[J].Composites Science and Technology,2000,50:1085-1094.
[6]SINKE J.Manufacturing of GLARE parts and structures[J].Applied Composite,2003,10:293-305.
[7]KAWAI M,MORISHITA M,TOMURA S,TAKUMIDA K.Inelastic behaviorandstrengthoffibre-metalhybrid composite:GLARE,International Journal of mechanical sciences,1998,40:183-198.
[8]彭文杰.复合材料层合结构极限强度预测方法及分层应力最小化研究[D].武汉:华中科技大学,2009.
[9]张朝晖.ANSYS 11.0结构分析工程应用实例解析[M].北京:机械工业出版社,2009.
[10]WU G,YANG J M.Analytical modelling and numerical simulation of the nonlinear deformation of hybrid fibremetal laminates[J].Modelling and simulation in materials science and engineering,2005,13:413-425.

