基于有限元法的Alberich型覆盖层吸声特性研究
商 超,魏英杰,张嘉钟,曹 伟
(哈尔滨工业大学航天学院,哈尔滨 150001)
1 引 言
Alberich型吸声覆盖层在水声中应用比较广泛,对水下航行器声隐身具有重要军事意义和使用价值[1-2],其基本结构是在高阻尼的黏弹材料层中嵌入周期性分布的2mm和5mm圆形空气柱腔。这种在基材内部嵌置共振吸声结构型式的吸声机理研究从四五十年代一直延续至今[3-10],仍在不断发展着。
Alberich型吸声覆盖层的吸声机理与声特性比较复杂,与材料的物理参数、空腔结构、温度、压力等因素密切相关。汤渭霖等[5]采用柱面波展开法,半解析地对含有周期短圆柱空的吸声覆盖层声学性能进行仿真,研究结果表明,柱腔内的轴对称波对覆盖层的低频消声特性具有重要贡献。Lane[6]通过改变穿孔层材料硬度的实验,提出谐振吸声主要取决于表面层弯曲振动,穿孔材料层只起到影响表面层边界支撑条件的次要作用。Gaunaurd[7]则认为表面层和穿孔层在谐振吸声中的作用大小跟材料相对硬度有关。如果表面层比穿孔层硬,就主要是孔壁的径向振动;如果相反,谐振吸声就主要取决于表面层的弯曲;如果表面层与穿孔层的硬度相差不大,那么这两种运动形式兼而有之。
对于几何形状稍复杂的消声瓦结构或带有其他粘弹性材料的消声瓦,声学特性没有解析解,需要用数值方法研究,多采用有限元方法,因为它能有效地求解微分方程的任意边值问题。Hennion[8-9]应用有限元法,对周期排列柔顺管和周期分布圆柱形空腔覆盖层的反射和透射特性进行了研究。Easwaran[10]认为流体介质可以作为弹性材料来处理,仅采用1/4个周期单元来划分网格,计算研究了双周期吸声结构的有限元计算问题。
本文基于有限元法研究了附在钢板上并以空气为背衬的Alberich型覆盖层的吸声特性。通过和无腔时的覆盖层吸声系数的解析解对比,证明了方法的可行性。与上述文章中有限元法不同之处在于,采用无反射流体吸声边界,以较少的单元很好地模拟了无限声学流场。最后针对一种小腔环绕大腔的混合型空腔结构开展了有限元分析,结果表明,该结构的吸声特性明显优于相同穿孔率的单腔结构。
2 理论模型
2.1 声场流固耦合问题
假定流体是可压的,但只允许压力与平均压力相比有较小的变化。而且,流体假定为非流动并且无粘的(即粘性不引起耗散作用)。假定平均密度和平均压力不变,压力求解偏离平均压力而不是绝对压力。
在声场流固耦合界面问题中,由于上述简化假设,流体的动量方程中法向声压梯度与结构的法向加速度在界面S处遵循以下规律:

其中{U}为结构在界面S处的位移;{n}为界面的单位法向量,由流体指向固体。
通过迦辽金方法得到完整的声场流固耦合问题的有限单元法方程为:
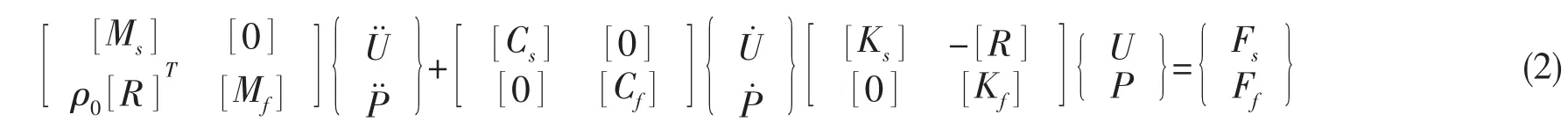
其中[R]是一个耦合矩阵,代表与流体—结构界面上的节点相联系的有效表面面积。
2.2 粘弹性材料吸声和流体边界吸声
Alberich型吸声覆盖层通常取用粘弹性材料(如橡胶)做基材,然而对于粘弹固体,拉密常数一般为复数,其虚数部分代表了材料中存在损耗因素,这时材料的各弹性参数都应表示成复数形式,如弹性模量E表示成一个复数:

其中η为弹性模量的损耗因子。由此刚度矩阵[K]改写成复刚度矩阵 [K~]:

阻尼矩阵[C]用刚度矩阵[K]和损耗因子η来表达:

其中ω为圆频率。
而流体阻尼矩阵[Cf]的表达式为

其中,c为流体声速;α为流体边界吸声系数;{}N为声压形函数。
当设置α的值为1时,流体边界即为无反射边界,可用于模拟无限流场。
2.3 反射系数和吸收系数
当平面声波垂直入射在平面分界面上时,声压反射系数R可以用下式计算:

其中,Z0=ρ0c0是入射平面波所在介质的波阻抗;Zb是吸声材料表面单位面积的机械阻抗。Zb一般为复数:

其中,p取声场流固耦合界面流体侧节点的压力,v取固体侧节点的法向速度。
求得反射系数R后,吸声系数α表示为

3 计算模型
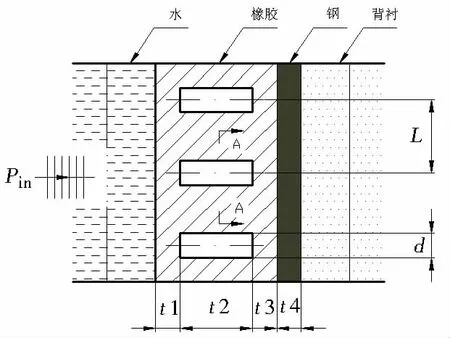
图1 模型结构示意图Fig.1 Sketch of structure model
数值计算采用的模型如图1所示。Alberich型吸声覆盖层(埋入双周期圆柱孔的橡胶层)敷设在钢板上,钢板后为水背衬或空气背衬。平面声波从水中垂直入射到吸声覆盖层上。
数值计算时取用如图2所示的一个周期胞元,算例均采用六面体网格,网格最大尺寸为2.5mm,有限元模型如3所示。
采用的吸声材料(橡胶)参数:杨氏模量Er=1.4e8Pa;杨氏模量损耗因子ηr=0.23;泊松比υr=0.49;密度ρr=1 100kg/m3。材料水的参数:密度ρw=1 000kg/m3;声速cw=1 489m/s。材料钢的参数:杨氏模量Esl=2.07e11Pa;泊松比 υsl=0.3;密度 ρsl=7 800kg/m3。
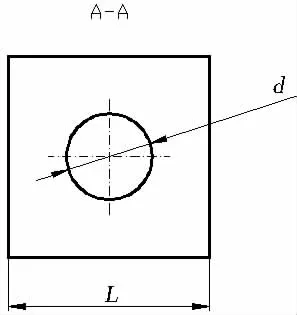
图2 A-A截面图Fig.2 Cross-sectional view of the section A-A of Fig.l

图3 胞元有限元模型Fig.3 Finite element model of the unit cell
何祚镛等在文献[4]中基于非均匀波导理论,对任意非均匀层,提出分层近似求传递矩阵的方法。该方法考虑的是等效波导截面,对于穿孔率相同的胞元计算得到的结果将是一样的。然而穿孔率相同的胞元可以具有各种结构形式,本文维持穿孔率不变的情况下尝试的图4和图5所示的结构,中间空腔半径变小,在其周围增加四个小腔,收效不错。
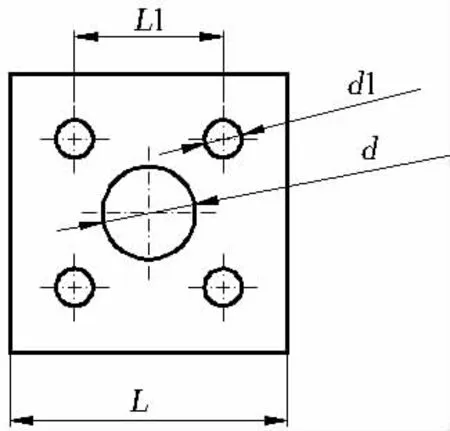
图4 工况1Fig.4 Case 1

图5 工况2Fig.5 Case 2
4 计算结果及分析
4.1 有效性验证及水层厚度的影响
均匀无腔覆盖层,厚度为t=50mm;钢板厚为5mm;水层厚度为7.5mm或75mm,用来模拟无限声学流场。计算结果如图6所示。其中解析解采用文献[3]中的方法,并在橡胶的纵波声速计算公式中考虑泊松比(约为0.5,而非0)的影响,使用公式:

从图6可以看出,本文的方法与解析解吻合得非常好。而且由于无反射流体吸声边界的设定,以较少的单元模拟无限声学流场已经具有很高的精度,而不必至少达到最大波长的0.2倍,因此可以减少计算量,提高计算效率。

图7 不同穿孔率下的吸声系数Fig.7 The absorption coefficient of different perforating rate
4.2 穿孔率对吸声特性的影响
胞元外部宽度L=30mm;覆盖层各部分高度t1=2mm,t2=46mm,t3=2mm;空腔直径d=6/10/12.8mm;钢板厚度为5mm。结果如图7~9所示。
由图7可以看出,随着穿孔率的变大,第一吸声峰值向低频移动,峰值变大变窄,但同时吸声谷底有降低趋势。相比较而言,6mm空腔覆盖层的吸声性能较好。由图8和图9可以看出,在空腔直径较小时,孔壁的径向振动和表面层的弯曲兼而有之;在空腔直径较大时,表面层的弯曲非常剧烈,孔壁的径向振动相对较小,但仍较6mm空腔的工况要大。振动主要发生在空腔附近。

图8 6mm空腔覆盖层在10kHz的振动模式Fig.8 The vibration modes of anechoic coating with 6mm cavity at 10kHz
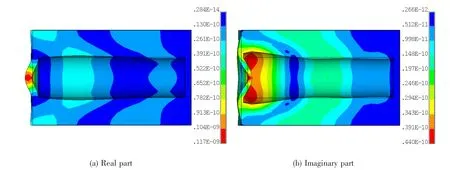
图9 12.8mm空腔覆盖层在10kHz的振动模式Fig.9 The vibration modes of anechoic coating with 12.8mm cavity at 10kHz
4.3 混合型空腔结构对吸声特性的影响
胞元外部宽度L=30mm;覆盖层各部分高度t1=2mm,t2=46mm,t3=2mm;空腔直径 d=10mm,d1=4mm;小空腔中心间距L1=16mm,L2=20mm;钢板厚度为5mm。结果如图10~11所示。
由图10可以看出,在低频段0~2kHz处,四种工况吸声性能相近;在频率段2~5kHz时,混合型空腔覆盖层的吸声性能也较10mm空腔的覆盖层稍差,但优于相同穿孔率的12.8mm空腔的覆盖层;在频率高于5kHz时,混合型空腔覆盖层的吸声性能明显占优。对于两种混合型空腔的工况,两者在5kHz后的吸声表现有所差异,但工况1在部分频率段具有明显优势,且在整体上相对平稳,故较好。由图11可以看出,大腔周围引入小腔,减小了孔壁厚度,使得覆盖层的振动整体加剧,谐振吸声效果更好。

图10 随频率变化的吸声系数Fig.10 Frequency variation of the absorption coefficient

图11 工况2的空腔覆盖层在10kHz的振动模式Fig.11 The vibration modes of anechoic coating with cavity of case2 at 10kHz
5 结 论
基于有限元法,研究了附在钢板上并以空气为背衬的Alberich型覆盖层的吸声特性。运用无反射流体吸声边界可以由较少的单元来模拟无限声学流场,减少计算量。在无腔时,本文的有限元法和解析解能够非常好地吻合。振动模式的结果直观,利于进行吸声机理的分析和作为结构优化的参考,从中可以发现,空腔附近存在相对剧烈振动,对吸声有重要的贡献。提出一种混合型空腔的思想,这种腔型的覆盖层的吸声性能优于相同穿孔率的单腔覆盖层。因此,通过合理优化胞元的空腔结构,Alberich型覆盖层的吸声性能将有很大的提升空间。
[1]张宏军,邱伯华,石 磊等.消声瓦技术的现状与发展趋势[J].舰船科学技术,2001,1(4):6-14.
[2]王旌生,吴有生.粘弹性复合材料结构水中振动及声辐射研究进展综述[J].船舶力学,2007,11(5):804-811.
[3]何祚镛,王 曼.水下均匀复合结构吸声的理论研究[J].应用声学,1996,15(5):6-11.
[4]何祚镛,王 曼.水下非均匀复合结构吸声的理论研究[J].应用声学,1996,15(5):12-19.
[5]汤渭霖,何世平,范 军.含圆柱形空腔吸声覆盖层的二维理论[J].声学学报,2005,30(4):289-295.
[6]Lane R.Absorption mechanisms for waterborne sound in Alberich anechoic layers[J].Ultrasonics,1981,19(1):28-30.
[7]Gaunaurd G C.Comments on ‘Absorption mechanisms for waterborne sound in Alberich anechoic layers’[J].Ultrasonies,1985,23(2):90-91.
[8]Hennion A C,Bossut R,Decarpigny J N.Analysis of the scattering of a plane acoustic wave by a periodic elastic structure using the finite element method:Application to compliant tube gratings[J].J Acoust.Soc.Am.,1990,87(5):1861-1870.
[9]Hennionand A C,Decarpigny J N.Analysis of the scattering of a plane wave by a doubly periodic structure using the finite element method:Application to Alberich anechoic coatings[J].1991,90(6):3356-3367.
[10]Easwaran V,Munjal M L.Analysis of reflection characteristics of a normal incidence plane wave on resonant sound absorbers:A finite element approach[J].J Acoust.Soc.Am.,1993,93(3):1308-1318.

