基于大涡模拟和Kirchhoff积分方法的孔腔流动发声机理分析
张 楠,沈泓萃,朱锡清,姚惠之
(中国船舶科学研究中心,江苏 无锡 214082)
1 引 言
流经孔腔的非定常流动经常出现在与流体力学相关的众多工业领域中。孔腔分陷入式与突出式两大类。陷入式孔腔是一种经典模型,在流体力学领域常见的大都是陷入式孔腔,经过几十年的试验研究与理论分析,人们对其流体动力特性和声学特性有了一定程度的认识。在实际工业应用中,一般都尽量避免出现孔腔流动,因为此时常伴有各类振荡,能够引起结构振动与疲劳,激发很强的噪声,而且由于从孔腔中向外抛射较大尺度的涡而造成物体压力脉动和阻力的急剧增加。孔腔流动包含了剪切层不稳定性,湍流与结构和流动噪声之间的相互作用等流固耦合、流声耦合复杂现象。由于流动和噪声之间的时空特征尺度相差很大,从而给理论分析、数值模拟和试验测量带来了很大的挑战。
在过去的五十多年里,这一类型的流动曾被广泛地研究过,最初的工作是Roshko在1955年所做的试验测量与分析[1]。Rossiter(1964)[2]给出了辨识流动模态振荡频率的公式,从而可以表征跨越孔腔开口处的混合层与压力场之间的耦合。在随后的岁月里,孔腔流激噪声的试验测量与数值预报在空气动力学领域逐步得到普遍关注,人们对此进行了大量研究,而在水动力学领域中的研究却相对较少。
近年来,在国际空气动力学领域,数值预报孔腔流激噪声并在数值预报的基础上探索控制流激噪声的措施逐渐成为研究的主流,而对于孔腔流激噪声机理的研究较少,基本还停留在早期的认识上。在孔腔绕流数值模拟领域,以前的研究者都采用无粘流即求解欧拉方程的方法,后来发展到非定常RANS数值模拟,近年来出现大涡模拟(LES)和直接数值模拟(DNS)。在早期,在低马赫数领域,研究者采用求解不可压缩RANS方程的模拟方法,耦合求解声学方程;在亚音速、跨音速和超音速状态下,许多研究者求解的是可压缩的RANS方程。随后,特别是进入本世纪以来,人们开始采用大涡模拟方法以及直接数值模拟方法,来计算孔腔流动和远场噪声。
Rossiter(1964)[2]与 Rockwell和 Naudascher(1978)[3]分析了孔腔绕流的流动机理。 他们认为,流体流经结构表面开口时,导边脱出自由剪切层撞击腔口随边产生压力反馈(pressure feedback),形成剪切层自持振荡(self-sustaining oscillation、self-controlled oscillation)现象。孔腔自持振荡可以分为三种类型:流体-动力(fluid-dynamic)振荡、流体-共振(fluid-resonant)振荡、流体-弹性(fluid-elastic)振荡。 自持振荡不但在腔内产生很强的振荡压力,还能发出很强的单频音(tone)。某些情况下,流体动力振荡可能与腔体的某阶声驻波共振的固有频率相吻合,导致声驻波的耦合共振(coupled resonance),从而引发强烈的声辐射,称为“哨音”(whistle),研究者也常把这种现象归为“流声耦合”(flow-acoustic coupling)现象中的一种(Knotts和 Selamet,2003)[4]。
长期以来,人们对于孔腔流激噪声的认识还基本停留在对上述三种振荡的一般理解上。近年来,水中孔腔流激噪声问题越来越受到船舶研究者的关注,那么,对于水中孔腔的流激噪声而言,这三种振荡在流激噪声形成的过程中各起到什么样的作用,以及孔腔流激噪声是如何向远场传播的,是亟待阐明的问题。本文在前期工作[5-6]的基础上,利用大涡模拟计算流场,并结合Kirchhoff控制面积分分析了水中孔腔流激噪声形成与传播的机理。文献[6]对于五种孔腔的流激噪声进行了计算,并采用中国船舶科学研究中心大型循环水槽测量结果验证了计算方法的可靠性,本文即针对文献[6]中的五种孔腔进行机理分析。详细的计算方法,包括大涡模拟方程与基于Kirhoff积分的FW-H方程远场解的描述请参见文献[7],在此不再赘述。

图1 4#与5#孔腔几何与网格Fig.1 Geometry and surface grid of cavity 4#&5#
2 孔腔流动发声机理分析
2.1 孔腔流动自持振荡分析
机理研究的目的在于揭示孔腔流激噪声的成因,以便最终实现有效的控制,问题的关键就是建立微观流动现象与宏观噪声响应间的联系。Rossiter(1964)[2]将孔腔中的自持振荡分为三种类型:动力振荡、共振振荡、弹性振荡。下面我们就上述三种类型的振荡逐一分析,找出本研究中孔腔流动辐射噪声的来源。
首先,计算中采用的是刚性壁面,孔腔没有变形,也不存在结构振动。试验模型也进行了加固和刚性处理,通过加速度传感器测量分析,可知也不存在结构振动。所以,那种由于结构变形和结构振动而引起的弹性振荡在本研究中没有出现,因而弹性振荡的影响可以不予考虑。
其次,我们知道,当流体动力振荡频率与孔腔深度方向的某阶声驻波共振的固有频率相吻合时,将发出极强的单频音,产生声驻波耦合共振,这种流/声共振将产生强烈的辐射噪声。
Rossiter(1964)[2]给出了辨识流体动力振荡模态频率的半经验公式:

其中,U0为来流速度,L为孔腔沿流向的长度,M为马赫数,n为模态阶数,fn为模态频率。
孔腔声驻波共振的固有频率为:

其中,C为环境声速,L为孔腔沿流向的长度,H为孔腔深度,n为模态阶数。
要注意的是水中声速Cwater≈1 500m/s,水中航行体的运动都是低马赫数或极低马赫数下的运动(一般M≈0.001~0.02),再考虑到水中航行体上常见孔腔的尺寸,可知上述流体动力振荡的模态频率和声驻波的固有频率之间相差很远,一般而言,不太可能出现上述的耦合共振,这是因为低马赫数下流体扰动传播波数不能与声扰动传播波数相匹配的原因所致。以2#孔腔为例,可以算得第一阶fA=14.2Hz,fB=1230.4Hz;以4#孔腔为例,可以算得第一阶fA=4.3Hz,fB=960.2Hz。可见fA与fB二者在数量级上相差甚远,其他各阶模态也有很大差异,不可能出现耦合共振。无论是从计算得到的孔腔流动辐射噪声频谱上,还是从试验得到的孔腔流动辐射噪声频谱上,都没有出现声谐振尖峰,说明耦合共振现象不存在,因而共振振荡的影响可以不予考虑。
综上所述,可以肯定地讲,本研究中孔腔发出的辐射噪声完全是由于流体动力振荡引起的。孔腔开口处存在自由湍流剪切层,孔腔周围为不连续的壁面湍流边界层,孔腔内为非定常的涡旋运动,它们三者相互作用,共同组成辐射噪声的声源。归根到底,还在于三者所包含的脉动剪应力、脉动压力与脉动速度,它们构成了最根本的偶极子声源与四极子声源,它们在辐射噪声中所起的作用将在下面讨论。
2.2 偶极子与四极子声源对声谱影响的辨识分析
许多声学方面的经典著作都曾指出,从理论上分析,低马赫数下四极子源的辐射效率很低,因而对于辐射噪声的贡献也很小,在总的辐射噪声中常可忽略,但是他们也同时指出,这主要是针对高频辐射噪声而言的。对于本文所研究的孔腔绕流,试验已经明确测量出流激噪声,如果按照上述理论分析,忽略四极子源对噪声的贡献,那么必然要将成因归结为低阶声源。文献[8]指出,流体流过阀门、格栅、孔腔等主要含偶极子声源。那么,对于孔腔噪声而言,四极子源在总的辐射噪声中占多少量级,四极子源对辐射噪声频谱又有哪些影响,是极待阐明的问题。本节在大涡模拟和声学类比的理论基础上,利用Kirchhoff控制面积分和物体壁面积分,分析了偶极子声源和四极子声源对流动辐射噪声的影响以及各自所占的份额。
首先,FW-H方程提供了分析流激噪声成因或分类的理论基础:
·单极子噪声:表征质量或体积力变化产生的噪声,反映单极子流动现象。
·偶极子噪声:表征表面力变化产生的噪声,反映偶极子流动现象。
·四极子噪声:表征Lighthill应力或雷诺应力变化产生的噪声,反映四极子流动现象。
下面从FW-H方程右边不同声源的数学表达上进行探讨,分析不同性质声源的特征。
在单极子声源的表达式方括号外含时间t的一阶导数,不含空间导数。表达式方括号中显含法向速度项,这说明只有当物面具有随时间变化的法向速度时,即物面存在变形和移动时,此项才存在,否则该项不存在。因而对于水动力学领域而言,脉动空泡可作为单极子声源。本文所研究的孔腔流激噪声,固壁都是刚性的,且没有随时间的移位变化,所以没有单极子声源,下面也不再讨论。
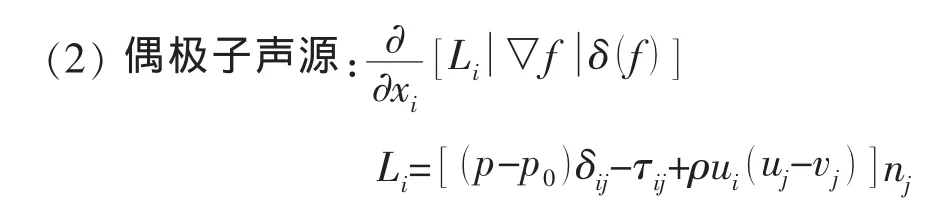

图2 4#孔腔内采样点位置Fig.2 Sampling positions in cavity 4#

图3 P1点脉动量能谱Fig.3 Power spectrum of fluctuation quantities on P1
在偶极子声源的表达式方括号外含空间的一阶导数,不含时间导数。表达式方括号中显含压力项、剪应力项和速度项。本文所研究的孔腔流激噪声,固壁都是刚性的,计算中满足法向无穿透、切向无滑移的物面条件,所以偶极子声源表达式中速度项的影响可忽略,仅剩下压力与剪应力两项。下面就采用大涡模拟方法,计算了如图2所示的4#孔腔壁面上4个点上的脉动压力和脉动剪应力,并做FFT变换,得到的能谱如图3~6所示。

图4 P2点脉动量能谱Fig.4 Power spectrum of fluctuation quantities on P2

图5 P3点脉动量能谱Fig.5 Power spectrum of fluctuation quantities on P3
从图3~6可知,孔腔内部的脉动压力能量大于脉动剪应力能量。依照声学经典理论可知偶极子源的辐射效率是确定的,因而从流动能向外场转化为声能的角度考虑,偶极子源表达式中压力项对流激噪声的贡献要大于剪应力项的贡献。

在四极子声源的表达式中含空间的二阶导数,不含时间导数。表达式中显含压力项、剪应力项和速度项。在低马赫数下,这三项对于辐射噪声影响的主次关系前人已经有了清晰的认识。Lighthill(1952)指出在低马赫数下,粘性应力τij是由动量的分子输运引起的,而雷诺应力ρuiuj则考虑了动量的非线性对流,可将 Tij简化为 Tij=ρuiuj[9-10]。 Obermeier(1985)与 Morfey(2003)[11]已经在定性和定量上都证实了Lighthill的处理是完全正确的。所以,低马赫数下四极子对噪声的影响都可归结到空间脉动速度的影响上。
在讨论了三种声源的性质之后,就利用Kirchhoff控制面积分(偶极子+四极子)和物体壁面积分(偶极子)定量辨识分析了两种声源对于流激噪声频谱的影响。分别计算了两种声源对于4#、5#孔腔声谱的影响。计算结果见图7~8。
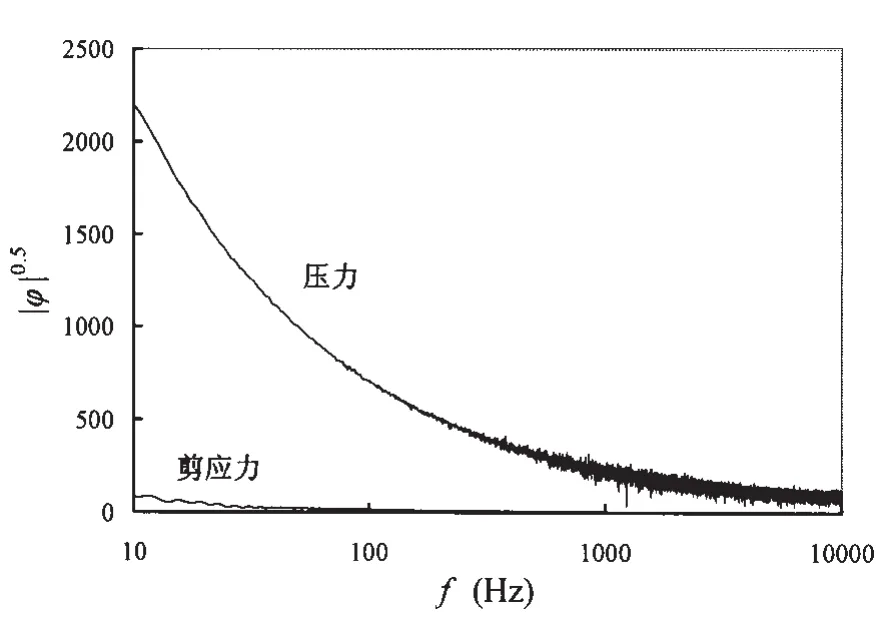
图6 P4点脉动量能谱Fig.6 Power spectrum of fluctuation quantities on P4

图7 4#孔腔声谱中的声源成分Fig.7 Sound source effect in the spectrum of cavity 4#
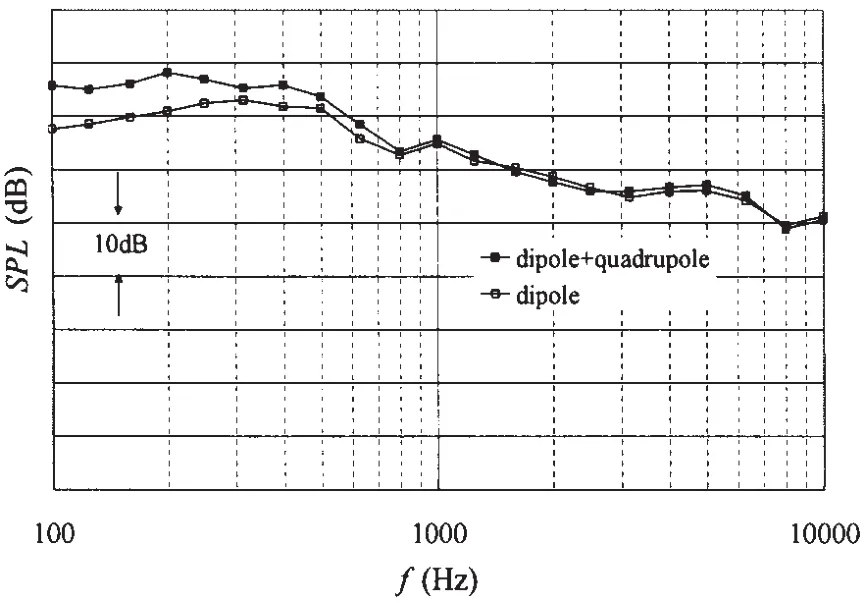
图8 5#孔腔声谱中的声源成分Fig.8 Sound source effect in the spectrum of cavity 5#
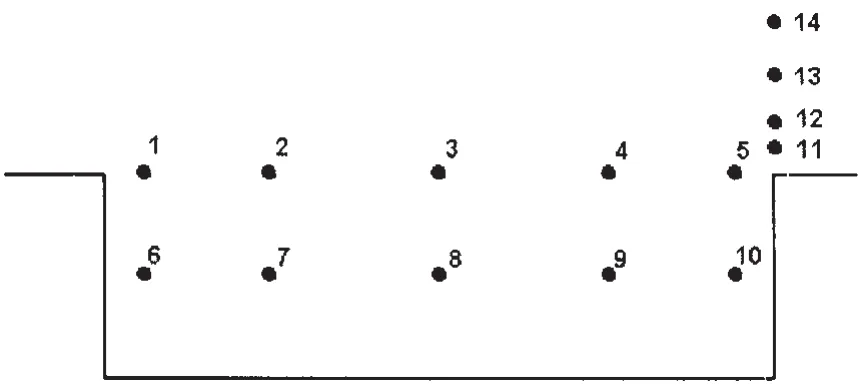
图9 4#孔腔内采样点位置Fig.9 Sampling positions in cavity 4#
从图7~8可以明显看出,由不同孔腔得到的结果都反映了同一个现象:即四极子源对于流激噪声频谱的影响主要在600Hz以下的低频段,其对于频谱有不同程度的增加,频率越低越显著;对于600Hz~10kHz的高频段,几乎没有明显影响,影响仅在1dB之内。这与经典声学著作上的理论分析基本一致。在下一节中将对Lighthill应力张量进行频谱分析,从而印证四极子源主要影响低频段流激噪声的结论。
2.3 Lighthill应力张量的频谱分析
本节对于4#孔腔内外14个位置处的Lighthill应力张量能谱进行了大涡模拟计算,首先得到随时间变化的时域信号,然后通过FFT变换得到频谱。14个采样点的位置如图9所示。
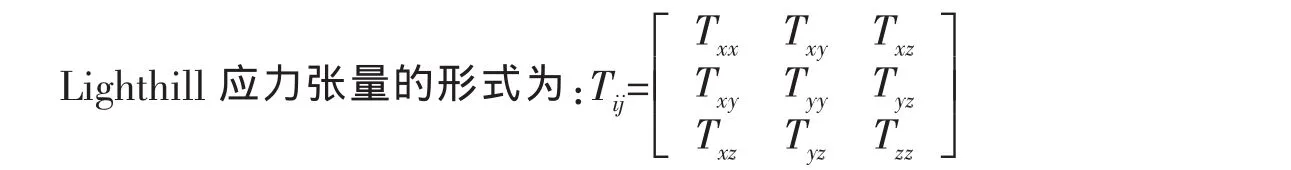
通过计算发现,这9个分量的频谱能量都集中在低频,结论基本一致,为了节省篇幅,不造成论文的冗长,本节仅给出11~14这四个点上Txy的能谱,计算结果见图10~13。

图10 11#采样点上Txy的能谱Fig.10 Power spectrum of Txyon sample 11#

图11 12#采样点上Txy的能谱Fig.11 Power spectrum of Txyon sample 12#

图12 13#采样点上Txy的能谱Fig.12 Power spectrum of Txyon sample 13#

图13 14#采样点上Txy的能谱Fig.13 Power spectrum of Txyon sample 14#
从计算分析可知,14个采样点上Txy能谱的形式与量级都有很大差异,这其实是孔内涡旋形式多样的直接体现。虽然Txy能谱有很大差异,但是14个采样点上的结果基本都反映了这样一个现象:Txy能量主要集中在600Hz以下的低频段,特别是10~100Hz这样的低频段,随着频率增高,其幅值迅速衰减。这与前述四极子源主要影响低频段流激噪声的结论是吻合的。11#~14#这四个采样点上Txy的能谱形式基本一致,近壁面第11点的能量最大,随着采样点远离壁面,则能量逐渐减小,说明Lighthill应力张量的能量主要集中在壁面附近,壁面的影响凸显出来。在下一节,我们将讨论壁面与涡在诱发流激噪声中的作用。
2.4 壁面与涡在诱发流激噪声中的作用
首先,对壁面在流动发声中的作用进行阐述。在固体壁面存在的情况下,特别是有压力梯度的壁面存在时,湍流声辐射将大为增强。这是因为当流动中有壁面存在,且其表面阻抗与流体不一致时,壁面的作用一方面在于通过反射声波来改变声场,另一方面,壁面也对局部流动引起干扰,使得表面压力作为偶极子声源向外辐射噪声。Curle与Powell从数学上阐明了上述观点。Curle方程表明,低马赫数下刚性壁面(rigid wall)对于辐射噪声的影响可通过在壁面位置上分布紧致的偶极子源来表征。壁面上的流体脉动压力包括水动力分量与声学分量,我们知道无压力梯度平板的直接声辐射是非常小的,完全可以忽略不计,当存在压力梯度时,辐射效率就会增强。紧致的物体固壁将作为偶极子声源向外辐射噪声,尖锐的边棱更是有效的辐射器。对于本文研究的孔腔流激噪声,虽然流速较低,然而孔腔开口边棱对声辐射也会起一定的作用。
流经刚性壁面上边界层中的压力与剪应力在噪声产生的过程中究竟起到什么作用,一直是声学研究中不断被讨论的问题。在没有物体存在情况下的自由剪切层中的脉动速度将以四极子源的形式直接辐射噪声(例如自由喷射湍流),但是,当存在物体时,剪切层与壁面相互作用将诱导产生壁面应力,从而产生声辐射。如果物体是刚性的且远小于声波波长,这些表面应力将产生典型的偶极子性质噪声。Curle方程虽然表明物体壁面上的脉动应力起到偶极子源的作用,但采用Curle方程计算流动噪声时,面积分经常发散,因而不太适合于数值模拟与评估。Powell(1960)使用刚性壁面格林函数将Curle的结果重新进行了整理,研究表明物面上的法向应力的确为偶极子性质的声源,这与Curle方程所指出的固壁的作用在于使四极子声源增强为偶极子声源的论断是一致的。
随后,声学类比方程右边偶极子表达式中的粘性剪应力的作用也被人们加以讨论。对于“粘性剪应力偶极子能不能作为有效声源”这一问题,人们经历了长期的争论,这一问题对于应用Lighthill理论而言是十分重要的。近年来,国外在并行运算基础上进行的一系列数值模拟研究可以清楚明白地回答这一问题。Shariff与Wang(2005)[10]研究了一个简化模型问题,考虑在一无限大平面区域中有个很小的壁面区域进行低马赫数下的切向正弦运动,这就诱导了在外部无限大静止流体区域中的声紧致的速度/涡量场。移动的壁面作用在流体上唯一的力就是粘性剪应力。Shariff与Wang数值求解了可压缩的NS方程,求出的偶极子声场与用Powell方程预报的几乎完全吻合。这一数值试验确立了流动剪应力为合理的偶极子声源。而壁面剪应力的发声机理在于将粘性底层的入射涡扰动转化为向外辐射的声。在此基础上,研究人员又进行了定量研究。Hu(2002,2003)[10]采用直接数值模拟计算了湍流槽道流与Couette流,将计算得到的声源数据代入Lighthill方程预报了远场噪声,结果表明,在较高马赫数M≤1的情况下,壁面剪应力引起的低频偶极子辐射噪声超过了四极子辐射噪声;在较低马赫数下,壁面剪应力和四极子的影响都不突出。依据上述数值研究结果所提供的证据,在边界层噪声计算中将脉动的壁面剪应力作为有效声源是完全合理的。
其次,对涡在流动发声中的作用进行阐述。在解释流动辐射噪声的物理机理时,我们不妨将Lighthill的声学类比理论与Powell的涡声理论结合在一起进行阐释。声学类比的一个不足就是声源在空间上的分布比较广阔,不够集中。涡量=▽×相对于雷诺应力而言,在空间分布上较为集中。原因在于涡旋周围有很大一部分流动可以看作势流,它们不会产生声,真正产生声的涡旋只占据很小的空间。
Powell(1964)[12]发现亚音速等熵流中声音的产生与涡的运动有关,在无空泡以及气泡流的情况下,湍流中能够有效地在远场产生辐射噪声的最本质部分就是涡。涡运动与界面上的流动不连续性密切相关,流动与壁面间有相对运动时,或两层流体间有相对运动时就会产生涡。涡使得流体运动相对强烈,而且产生掺混。当涡相对声介质产生变形或加速时就会产生声辐射。涡声理论最初应用在低马赫数下自由空间内的辐射噪声问题。涡声方程虽然只是低马赫数下Lighthill声学类比方程的一种特殊形式,但是其强调了涡量的作用,而且鲜明地指出涡是一种偶极子性质的声源。
Powell方程表明如果刚性壁面引起了涡旋流动时,远场声压由下述四部分贡献组成:①表面分布的偶极子源,其强度正比于表面上的脉动压力p′。② 体积分布的偶极子源,其强度正比于体分布的×。③ 体积分布的无方向的源项④ 单极子源项,其强度正比于表面在自身外法向上的加速度∂un/∂t。考察上述四项可知,第三项是由于熵脉动引起的,对于本文研究的孔腔绕流该项不存在;第四项含有壁面法向速度的时间导数,也不存在。所以第一、二两项才是本文研究的孔腔涡旋流场诱导辐射噪声的主要贡献。
对真实流体而言,粘性是促使涡旋产生、发展、消失的最经常也是最重要的因素,绝大多数粘性流体运动都是有旋运动,因此研究涡旋在粘性流体发声中的效应具有重大意义。Powell指出将涡运动区域作为声源将大大增强人们对湍流引起噪声物理机理的理解。在粘性流体中,由于粘性作用,涡旋强的地方将向涡旋弱的地方输送涡旋,直到涡旋强度相等为止,因此理想流体中涡旋的保持性发生变化,出现的是涡旋扩散现象。涡旋的扩散与输运不但感生速度场使整个流动状态发生变化,而且也能将近场内的声学效应输送到远场。对于孔腔绕流,流激噪声的根源就在于绕流所产生的强烈的、形式各样的、尺度不等的涡。涡的运动与发展诱导了空间内的脉动速度、脉动压力和脉动剪应力(诱发机制),同时涡本身具有的输运与演化特性(传输机制),又将上述三者的近场扰动(变化率)产生的声学效应传递到了远场,最终转化为辐射噪声中的各个分量。
3 结 语
流动辐射噪声问题早已出现,但时至今日,人们仍无法完全理解其复杂性,更不用说彻底解决这一问题,因为它涉及到流体力学领域中最难处理的湍流和流动分离问题,牵扯到流固耦合和流声耦合等复杂现象。近代以来,经过Lighthill等众多前辈苦心孤诣的研究,目前已经开辟出了一个极富挑战性与启发性的研究领域,深藏在流激噪声背后的深刻的流/声机理正吸引更多的研究者投身其中。
本文在前期工作的基础上,对于水中孔腔的流激噪声机理开展了研究。经由孔腔内外多种流体振荡模态特征及其与流激噪声频谱特性的内在联系分析,明确指出在水中低马赫数情况下,流体共振模态极难发生,而流体动力振荡将是孔腔发声的主要来源,揭示了孔腔流激噪声形成的机理。提出了基于Kirchhoff控制面积分与物体壁面积分辨识孔腔流动中偶极子和四极子声源对流激噪声影响量级以及频谱分布规律的分析方法。并结合流体动力声源的数学表达以及Lighthill应力张量的频谱分析,详细讨论了偶极子、四极子流动现象与应力能量及相应流激噪声响应之间的关系,并指出了孔腔流场中的涡旋对于脉动压力、脉动剪应力、脉动速度声学效应的输运作用是产生远场辐射噪声的根源,从而揭示了孔腔流激噪声传播的机理。希望本文的工作能有益于未来的研究。
[1]Roshko A.Some measurements of flows in a rectangular cutout[R].NACA TN 3488,1955.
[2]Rossiter J E.Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[R].Rep.Mem.3438,Aeronautical Research Council,1964.
[3]Rockwell D,Naudascher E.Review-Self-sustaining oscillations of flow past cavities[J].Transactions of the ASME,1978,100:152-165.
[4]Knotts B D,Selamet A.Suppression of flow-acoustic coupling in sidebranch ducts by interface modification[J].Journal of Sound and Vibration 265,2003:1025-1045.
[5]张 楠,沈泓萃,姚惠之,朱锡清,俞孟萨.孔穴流激噪声的计算与验证研究[J].船舶力学,2008,12(5):799-805.
[6]张 楠,沈泓萃,朱锡清,姚惠之,谢 华.三维孔腔流激噪声的大涡模拟与声学类比预报与验证研究[J].船舶力学,2010,14(1):181-190.
[7]张 楠.孔腔流动和流激噪声机理及耦合计算方法研究[D].无锡:中国船舶科学研究中心,2010.
[8]马大猷,沈壕编著.声学手册[M].北京:科学出版社,1983.
[9]Crighton D G,Dowling A P,Ffowcs Williams J E,Heckl M,Leppington F G.Modern methods in analytical acoustics[M].Springer-Verlag London Limited,1992.
[10]Wang Meng,Freund J B,Lele S K.Computational prediction of flow-generated sound[J].Annu.Rev.Fluid Mech.,2006,38:483-512.
[11]Morfey C L.The role of viscosity in aerodynamic sound generation[J].Int.J Aeroacoustics,2003,2(3-4):225-240.
[12]Powell A.Theory of vortex sound[J].J Acoust.Soc.Am.,1964,36(1):177-195.

