基于Boussinesq问题解的锚索受力分析

郑小毅 武金博

（中交第二公路勘察设计研究院有限公司 武汉 430056）

0 引 言

预应力锚索作为一种重要的锚固支护技术，在改善岩土体应力状态，提高岩土体的整体性、承载力及稳定性等方面已为大量的工程实践所证实，广泛地应用于地质灾害加固的各个领域.但由于岩土体的复杂性，预应力锚索作用机理十分复杂，影响因素众多，目前关于预应力锚索作用机理及设计理论还很不完善，远远满足不了工程实践的需要，因此了解锚索的内力分布将对锚索设计有很大帮助，同时将带来显著的经济效益.

1 受力机理分析

假设岩土体为无限弹性空间体，锚索张拉力为一作用于岩土体表面的垂直集中力，则此问题可以看成为Boussinesq问题.在半无限体表面受法向集中力作用下，如图1所示，用位移法求解，即解空间轴对称体的Lame方程.

Boussinesq找到了满足上式的两组特解，即满足上述平衡方程的两组位移函数，分别为

代入得

根据位移互等定理，在O点作用力P产生M点的位移等于M点作用力P产生O点的位移，取锚固体与Z轴重合，此时R＝z，则端点的位移为

设锚固段对岩体产生的剪应力为τz，取一微小单元如图2所示.

dP＝2aπτ（z）dz，则τz引起的锚固段点O的位移为

图2 轴力－剪应力平衡图

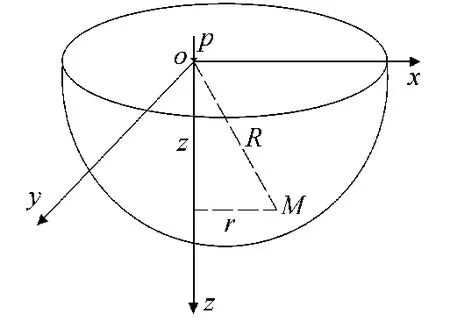
图1 Boussinesq问题示意图

锚固段总的总伸长量为

锚固段与岩体的变形都处于弹性状态，满足变形协调条件，则

两边同时对z求导，简化可得二阶变系数齐次常微分方程

借助MATLAB求解得出

有边界条件z＝0时τz＝0可得C2＝0.

沿锚索体积分可得轴力为

这与尤春安等人［1－3］基于Kelvin问题的推导结果公式相似.

锚固段位移积分得

2 应力分布形式及影响因素

2.1 应力分布形式

假设P＝960kN；a＝0.075m；υ＝0.25；E／Ea＝0.644 4，则得到k＝13.08，绘制分布曲线，如图3所示.由图3可知，轴力在锚固段端口处最大，然后快速衰减，直至趋于0，而剪应力在端口处为0，然后快速增大，在距端口0.5m位置左右到达极值，而后又迅速衰减，直至趋于0.

图3 锚固段应力分布曲线

2.2 钻孔半径的影响

其他参数不变，取不同的a（分别为0.0575，0.0675，0.075mm）得到钻孔半径对应力分布的影响如图4所示.

2.3 介质弹性模量的影响

岩石的E一般为0.95～83GPa，故E／Ea的变化范围一般为0.0266～2.3253，假设其他参数不变，取E／Ea分别为0.0266，0.6444，2.3253.E／Ea的变化对应力分布的影响如图5.

图4 钻孔半径a对锚固段应力分布的影响图

图5 E／Ea对锚固段应力分布的影响图

2.4 材料泊松比的影响

一般材料的泊松比υ变化不大，弹塑性材料的υ一般值为0.1～0.4，分别取υ为0.1，0.25，0.4.算得k值分别为13.27，13.08，13.41，相差不大，由此可知其对应力分布影响较小.

2.5 注浆压力的影响

锚索的锚固段一般都在很深的基岩中，由于开孔的影响，会使岩体的天然应力的平衡状态破坏，从而造成围岩应力的重分布，这些岩石可以近似认为各向同性的线弹性体，其应力从分布可以用弹性力学方法计算［4－5］.

当无注浆压力时，此时可以按平面应变问题考虑，引用柯西课题求解.计算图示如图6.

图6 无注浆压力计算图

此时砂浆处于无围压状态，抗剪强度没有提高，在这种情况下如果张拉吨位过大容易发生锚索与砂浆整体一起被拔出.当张拉时，对于压力型锚索来说砂浆受压，其应变为

而岩石由于开挖所产生的径向应变为

两式相等得

式中：σr为围压；σ0为天然应力；σz为锚索在承压板处的应力；υme为砂浆的泊松比；Eme为砂浆的弹模；υ为围岩的泊松比；E为围岩的弹模.

传统理论认为的在不考虑剪滞效应情况下砂浆无围压，黏结力仅有砂浆与岩面的绞合力提供，其值一般取围岩单轴抗压强度的10%.事实上当张拉完成后，砂浆既处于有围压状态，其抗剪强度和黏结力都有所提高.

当有注浆压力时，其附加应力可用弹性厚壁筒理论来计算，计算模型如图7所示.

图7 有注浆压力计算图

σr即为围压，它使得砂浆处于空间应力状态，对改善应力重分布，提高砂浆的抗剪强度是很有益处的.其力学模型如图8所示［6－7］.

图8 砂浆体受力模式图

当注浆压力为σ′时，由于岩石的弹模比砂浆的大很多，可以假设岩石不变形，既εr＝0，于是可得到

当张拉时砂浆应变为

而岩石由于开挖所产生的径向应变为

两式相等得

3 结 论

1）拉力型锚索的的应力分布规律是在端口处剪应力为0，然后顺速增大，并在靠近端口约0.5m的时候达到最大值，然后有快速的减小到0.而轴力在端口处为最大值，然后衰减为0.这与以前学者们研究的结论是一致的.

2）钻孔半径越小剪应力极值越大，分布范围越小，曲线越陡，应力集中现象越明显.故在实际工程中在条件许可的条件下可适当考虑增加钻孔半径来减小应力集中现象.

3）弹性模量比对应力分布的影响很大.比值越小即岩体越软，应力分布较均匀，分布范围较广，这与传统设计中采用剪应力平均分布相一致，故传统理论在软岩中设计的值是合理的.比值较大即岩体坚硬时，曲线陡峭，分布范围较小，集中现象明显，这时就不可以采用传统设计理论.

4）一般材料的泊松比υ变化不大，弹塑性材料的υ一般值为0.1～0.4，分别取为0.1，0.25，0.4.算得k值分别为13.27，13.08，13.41，相差不大，由此可知其对应力分布影响较小.

5）在软岩中应力分布范围较广，而在硬岩中分布范围较小.整体而言分布范围大约为0～5.5 m内，这说明锚固段锚索体的其它部分对应力无影响，即对锚索的极限抗拔力无贡献，故设计时可以减小长度，节约材料和造价.

6）注浆压力可以提高砂浆的围压，使其处于空间应力状态，从而提高砂浆的抗剪强度，减少在张拉时发生锚索被拔出的情况；同时在张拉完成后可以增加砂浆和岩面的黏结力，从而提高抗拔力.

［1］尤春安，战玉宝.预应力锚索锚固段的应力分布规律及分析［J］.岩石力学与工程学报，2005，24（6）：925－928.

［2］冯杨文.预应力锚索有关问题的分析研究［J］.探矿工程：岩土钻掘工程，2005，32（B09）：119－123.

［3］徐前卫，尤春安，朱合华.预应力锚索的三维数值模拟及其锚固机理分析［J］.地下空间与工程学报，2005，1（2）：214－218.

［4］云舟工作室.MATLAB 6数学建模基础教程［M］.北京：人民邮电出版社，2001.

［5］李同林，殷绥域.弹塑性力学［M］.武汉：中国地质大学出版社，2006.

［6］Makris N，Zhang J.Rocking response of anchored blocks underpulse－type motions［J］.Journal of Engineering Mechanics，2001，127（5）：484－493.

［7］黄 豪，唐小兵，张开银，向木生.竖向预应力作用效果的数值模拟与预应力损失的试验研究［J］.武汉理工大学学报：交通科学与工程版，2007，31（5）：922－924.