行波效应对大跨多塔悬索桥地震反应的影响分析＊

邓育林 何雄君

（武汉理工大学交通学院 武汉 430063）

对于大跨悬索桥的行波效应，许多学者进行了研究，Nakamura等［1］采用多点激励的反应谱方法，以及复杂的三维有限元模型，对金门大桥进行了地震反应分析，他们指出，对于大跨悬索桥，由于其柔性的影响，动力反应分量是主要的.此外，行波效应和多点激励对动力反应分量有显著的影响.对于两塔的反应，多点激励会导致较小的结果.A.A.Dumanoglu等［2］对3座欧洲大跨箱梁悬索桥进行了行波效应的比较分析，结果发现，在悬索桥的某些部位，行波效应会大大增加地震反应.胡世德等［3］通过对江阴长江大桥的地震反应分析指出，行波效应会使结构的反应增大.丰硕等［4］以构想中的1座主跨跨度达3 000m的悬索桥为研究对象，探讨行波效应对超大跨度悬索桥地震反应的影响.本文以泰州长江公路大桥为工程背景，分析行波效应对大跨多塔悬索桥地震反应的影响，并比较行波作用下不同结构体系地震反应的变化规律.

1 计算模型

泰州长江公路大桥为一座大跨3塔悬索桥，总体布置图见图1.2个主跨跨度均为1 080m，主缆的分跨为390m＋1 080m＋1 080m＋390m，加劲梁采用封闭式流线型扁平钢箱梁.边塔为混凝土塔，索塔总高178.0m；中塔为变截面钢塔，索塔总高192.0m，横桥向为门式框架结构，纵向为人字型.在边塔下横梁上设置竖向和侧向支座.边塔采用46根D3.1／D2.8m变截面钻孔桩群桩基础，中塔采用倒圆角的矩形沉井基础.

图1 三塔悬索桥布置图（单位：m）

2 行波效应影响分析

关于地震行进波速，现在学者们普遍认同应取视波速，而不是以前普遍采用的土层剪切波速，本次分析地震行进波速从150m／s开始，考虑到本桥南北两锚碇间距离很大，达2 940m，为较全面地分析地震行波效应的影响，最高波速取8 000 m／s，且依次取150，250，500，750，1 000，1 500，2 000，2 500，3 000，4 000，5 000，6 000，7 000和 8 000m／s 14个地震行进波速进行了分析，由于结构的对称性较好，本次分析仅考虑地震波从北端向南端传播.

2.1 对主塔内力反应的影响

图2、图3分别给出了地震动行进波速的变化对北塔塔底、南塔塔底以及中塔塔底截面内力的影响，图中纵坐标表示的是考虑行波效应与不考虑行波效应地震反应的比值，μ为12条波的平均值，σ为12条波的方差.

图2 地震行进波速对塔底截面剪力的影响

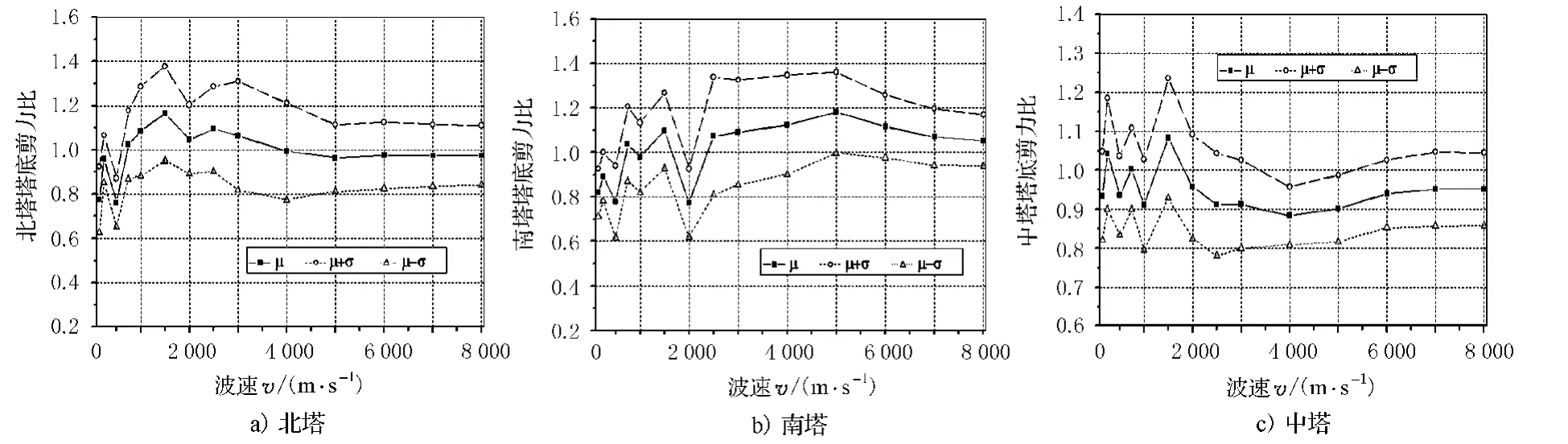
图3 地震行进波速对塔底截面弯矩的影响

从图2、图3可以看出：对于边塔，考虑行波效应有时会增大其地震反应，有时也会其减小地震反应，而对于中塔，考虑行波效应总体上减小其地震反应.当波速不断变化时，北塔塔底截面剪力平均值变化幅度为0.90～1.10，弯矩平均值变化幅度为0.75～1.15；中塔塔底截面剪力平均值变化幅度为0.9 0～1.1 0，弯矩平均值变化幅度0.90～1.10；南塔塔底截面剪力平均值变化幅度为0.70～1.25，弯矩平均值变化幅度为0.80～1.20.考虑地震波的变异性，北塔塔底截面剪力最大增大28%，弯矩最大增大40%；南塔塔底截面剪力最大增大42%，弯矩最大增大35%；中塔塔底截面剪力最大增大30%，弯矩最大增大25%.

2.2 对基础地震反应的影响

图4、图5分别给出了地震动行进波速的变化对北塔基础反力、南塔基础反力和中塔基础反力的影响，图中纵坐标表示的是考虑行波效应与不考虑行波效应地震反应的比值，μ为12条波的平均值，σ为12条波的方差.

从图4、图5可以看出：行波效应对边塔基础的水平反力影响不大，在个别波速情况下，对于北塔，平均值最大增加5%，考虑行波效应的变异性，最大增加15%，对于南塔，平均值最大增加7%，考虑行波效应的变异性，最大增加15%；行波效应对边塔基础的反力矩影响较大，对比图2和图3可以看出，其影响规律与对边塔塔底弯矩基本一致，但影响程度略小一点；行波效应对中塔基础的水平反力影响甚微，对反力矩影响也不大，即使考虑行波效应的变异性，最大增大也只有10%，且在大多波速情况下行波效应减小了中塔基础的水平反力及反力矩.

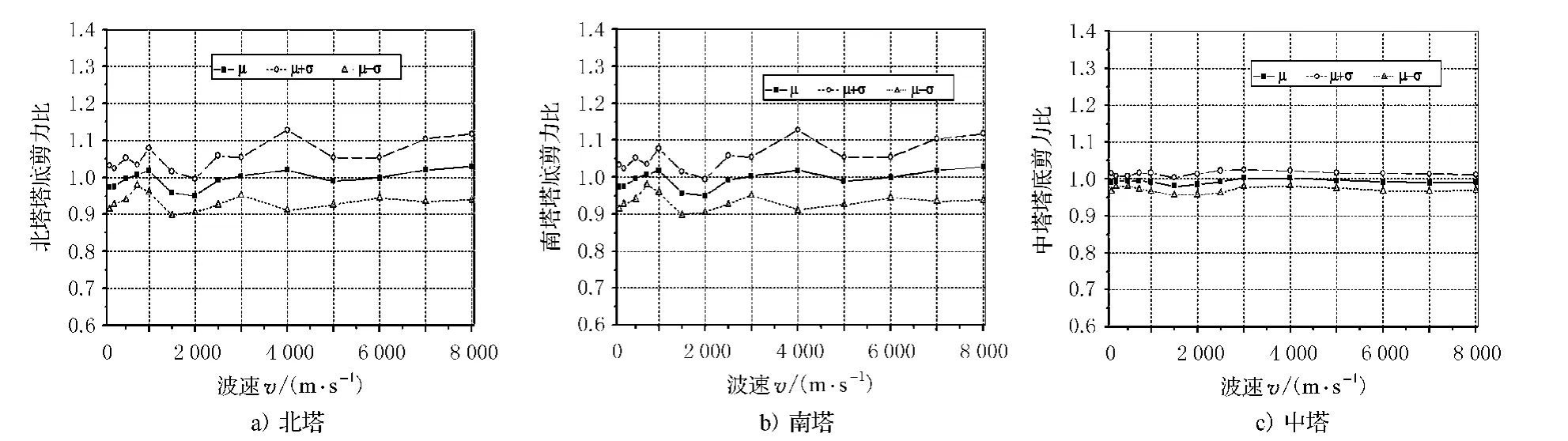
图4 地震行进波速对主塔基础水平反力的影响

图5 地震行进波速对主塔基础反弯矩的影响

2.3 对塔顶主缆抗滑移安全系数的影响

图6分别显示了地震行进波速的变化对边塔、中塔塔顶主缆抗滑移安全系数的影响，图中纵坐标表示的是考虑行波效应与不考虑行波效应地震反应的比值，μ为12条波的平均值，σ为12条波的方差.当比值小于1时表示行波效应对主缆抗滑移不利，反之大于1表示行波效应对主缆抗滑移有利.分析时主缆与鞍座鞍槽之间的摩擦系数μ取0.2.

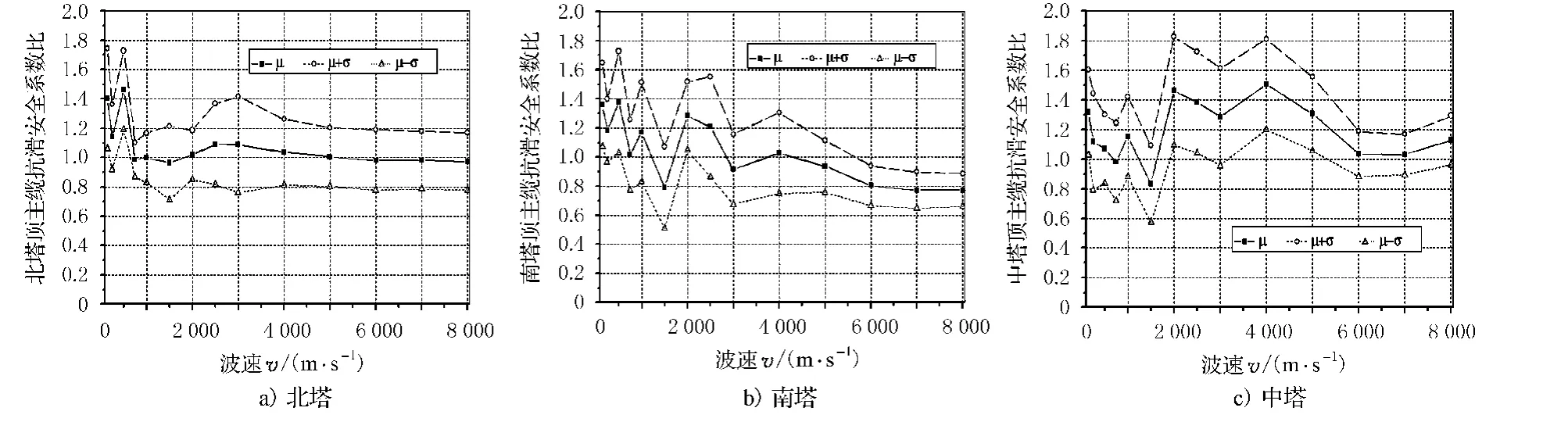
图6 塔顶主缆抗滑移安全系数比

从图6可以看出：行波效应对北塔塔顶主缆抗滑移安全系数影响较小，且基本上都是对主缆抗滑移有利；而对南塔塔顶主缆抗滑移安全系数有一定的影响，在个别波速情况下，行波效应平均值最大使主缆抗滑移安全系数减小20%左右，考虑结果的变异性，最大使主缆抗滑移安全系数减小50%左右，应当予以重视；行波效应对中塔塔顶主缆抗滑移安全系数也有一定的影响，但大多数情况都是对主缆抗滑移有利，只有个别波速情况下，行波效应平均值最大使主缆抗滑移安全系数减小20%左右，考虑结果的变异性，最大使主缆抗滑移安全系数减小40%左右.

2.4 对梁端位移的影响

图7给出了地震行进波速的变化对梁端位移的影响，图中纵坐标表示的是考虑行波效应与不考虑行波效应地震反应的比值，μ为12条波的平均值，σ为12条波的方差.从图8可以看出，行波效应对梁端位移的影响很小，行波效应平均值最大使梁端位移减小3%左右，考虑结果的变异性，最大使梁端位移变化也在7%左右.

图7 地震行进波速对梁端位移的影响

3 结构体系变化对行波效应的影响

图8、图9分别给出了四个模型，地震动行进波速的变化对北塔塔底、南塔塔底和中塔塔底地震内力的影响，取12条波的平均值，图中纵坐标表示的是考虑行波效应与不考虑行波效应比值.

图8 地震行进波速对塔底截面剪力的影响比较

图9 地震行进波速对塔底截面弯矩的影响比较

从图8、图9可以看出：当中塔基础形式不变时，无论中塔与主梁之间是否设置弹性索，行波效应对边塔塔底地震反应的影响规律及影响程度基本一致，即中塔、梁纵向连接方式的变化不会明显改变行波效应对边塔塔底地震反应的影响规律；而如果中塔、梁纵向连接方式不变时，中塔基础采用桩基础时，行波效应对边塔塔底地震反应影响要显著一些，特别是对边塔塔底剪力的影响，行波效应使得塔底剪力平均值最大增大25%左右，而当中塔基础采用沉井基础时，这一数值为15%左右.

从图8、图9还可以看出：当中塔采用沉井基础时，行波效应对中塔与主梁之间设置弹性索时的影响程度比中塔与主梁之间不设置弹性索显著；而当中塔采用桩基础时，无论中塔与主梁之间是否设置弹性索，行波效应对中塔塔底地震反应影响规律及影响程度相差不大；如果中塔、梁纵向连接方式不变时，中塔基础采用沉井基础时，行波效应对中塔塔底地震反应影响要略微显著一些.

上面分析表明，当中塔由沉井基础变为桩基础时，由于中塔整体刚度减小，边塔与中塔刚度比增大，使得行波效应对边塔的地震反应影响增大；而当中塔与主梁之间设置弹性索，中塔由桩基础变为沉井基础时，由于中塔刚度增大，边塔与中塔刚度比减小，使得行波效应对中塔的地震反应影响增大.

4 结 论

1）行波效应对边塔的地震反应有一定的影响，在个别波速情况下，行波效应使得边塔塔底反应增加40%左右；而行波效应对中塔的地震反应影响不大，且在大多波速情况下行波效应减小了中塔的地震反应.

2）行波效应对边塔基础的水平反力影响不大，但对边塔基础的反力矩有一定的影响，其影响规律与对边塔塔底弯矩基本一致，但影响程度略小一些.行波效应对中塔基础的水平反力影响甚微，对反力矩影响也不大，且在大多波速情况下行波效应减小了中塔基础的地震反应.

3）行波效应对梁端位移的影响很小，行波效应平均值最大使梁端位移减小3%左右，考虑结果的变异性，最大使梁端位移变化也在7%左右.

4）当中塔由沉井基础变为桩基础时，由于中塔整体刚度减小，边塔与中塔刚度比增大，使得行波效应对边塔的地震反应影响增大.

5）当中塔与主梁之间设置弹性索，中塔由桩基础变为沉井基础时，由于中塔刚度增大，边塔与中塔刚度比减小，使得行波效应对中塔的地震反应影响增大.

［1］Nakamura Y，Kiureghian A D，Liu D.Multiple－support response spectrum analysis of the golden gate bridge［R］.University of California at Berkeley，Report No.UCB／EERC－93／05，May，1993.

［2］Dumanoglu A A，Brownjohn J M W，Severn R T.Seismic analysis of the fatih sultan mehmet suspension bridge［J］.Earthquake Engineering and Structural Dynamics，1992，21：881－906.

［3］胡世德，范立础.江阴长江公路大桥纵向地震反应分析［J］.同济大学学报，1994，22（4）：434－438.

［4］丰 硕，项贻强，谢 旭.超大跨度悬索桥的动力特性及地震反应分析［J］.公路交通科技，2005，22（8）：31－35.

［5］Zerva A.Response of multi－span beams to spatially incoherent seismic ground motions［J］.Earthquake Engineering and Structural Dynamics，1990，19：819－832.

［6］Ettouney M，Hapij A，Gajer R.Frequency－domain analysis of long－span bridges subjected to nonuniform motions［J］.Journal of Bridge Engineering，2001（11／12）：577－586.