考虑路段转向流量和破坏排队的动态网络装载问题*
李曙光 周庆华
(长安大学电子与控制工程学院1) 西安 710064) (陕西交通职业技术学院公路工程系2) 西安 710021)
动态网络装载即是将时变的OD需求通过OD对之间的路径装载到路网中,获得路网中的路段路径的交通状况.目前对于动态交通网络装载问题的研究,从宏观模型而言,主要分为两类:一个是使用点排队模型[1-4],模拟单一模式或是多种交通模式车辆在路网中的运行状况,而点排队模型由于假设车辆是没有长度的点,忽视了由于车辆排队拥挤引起的破坏排队状况,因而,可能在一些情况下,低估路段交通拥挤状况.另一类是以简单的交通流动力学模型为基础[5-8],假设路段上仅有2种交通状况存在,一种是拥挤状态,另一种是车辆自由流状态,以此模拟车辆在路段上以及十字路口分流时的交通状况.本文在其基础上对分流模型的主要特性进行了分析,给出了相应的路网模型并在一个路网中进行了仿真试验.
1 路网模型描述
1.1 路段可接收和退出流量
一个有n个节点,和l有向路段的普遍路网结构G=(N,L).式中:N为节点集合;L为有向路段的集合.路段由变量a表示,路径由变量p表示,路径是无圈的,是由连接在一个起点与终点之间的OD对i个有向路段连接而成,p={a1,a2,…,ai}.RS表示旅行者的OD对的集合.连接OD对rs之间的路径集合用Prs.假设所有起点对应的节点没有入口路段,所有终点对应的节点没有出口路段,按照点排队方法模拟起点的排队行为.
研究时间区域[0,T]被划分为K个等时间长度的时间间隔数,时间间隔数的长度为T,“k”表示时间间隔[(k-1)·δ,k·δ].假设:研究时间区域足够的长,以便于所有的车辆在研究时域内都能够退出路网;时间间隔长度足够的短,以便于逼近连续时间模型;在一个给定的时间间隔期间、路段或路径流量率是恒定的.
文献[8]给出了累计车辆数与流量波速度之间的关系,即路段上只有2种流量波:一个是前向波,也就是路段车辆的自由流运行状态,前向波速度就是车辆的自由流速度,这与点排队的自由流速度是一致的;另一种是后向波,是由于路段出口容量的限制,而导致路段拥挤流量从路段出口向路段入口的流量传播过程,相应的后向波速度就是拥挤流量向路段入口传播的速度,本文虽然对路段出口转向排队分别进行处理,也就是说路段在出口处可能有多种拥挤状态存在,但是随着排队的向后转播,这些排队还是融为一种拥挤状态,也可以认为路段只有一种后向波.
在破坏排队的概念下,由于路段上的排队向后传播,进而可能导致上游路段的容量发生变化.下面进一步给出破坏排队概念下的路段流量传播以及节点容量分配方法.
遵从于文献[7-10]的方法,可能路段入口流量(也可以称为路段入口容量)不但受到路段入口容量的限制,(最大的路段保存容量),同时还可能受到路段下游排队的影响,当路段出口的排队一直延伸到路段入口时,相应的可能路段入口流量Xa(k)可以表示如下.

进一步,在间隔数k路段的基于转向的可能出口转向流量主要包括两个部分,一个是在k-时刻路段的入口流量以及在间隔数k-1由于路段出口拥挤未退出路段的车辆,qai,bj(k-1),相应的计算公式表示如下.

在间隔数k路段转向排队车辆数的计算表示如下.

相应的可能路段路径出口流量和路段排队车辆数可用下式表示

1.2 节点流量分配模型
节点流量分配模型是根据路段的出口容量,转向流量以及下游路段的可接收流量确定路段的时变出口容量,然后使用路段时变的出口容量计算相应的路段路径出口流量率.为了简化描述,首先给出简单的“合流”与“分流”节点的节点流量分配模型.
对于分流节点n,只有一个路段ai进入这个节点,有j个退出路段b1,…,bj.相应的路段转向出口容量表示如下.

路段出口处的转向容量受到下游转向分支路段可接受流量以及路段ai所提供的转向路段bj的容量的限制.
对于合流节点n,包括i个入口路段a1,…,ai,与一个出口路段bj.相应的路段出口容量可以表示如下.
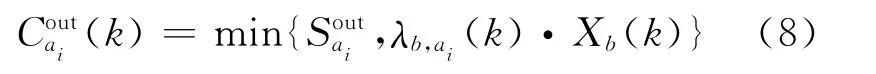
式中:λb,ai(k)表示路段b分配给路段ai的容量,为了简化期间,使用根据容量的固定合流比例也可以采用其他合流比例如文献[8-9]给出的方法.
下面给出具有多个入口路段a1,…,ai,和多个出口路段b1,…,bj的普遍节点的容量分配方法.相应的时变出口容量计算公式表示如下

上式与单独的合流与分流节点的计算方法一致.
实际的路段路径流量计算表示如下.
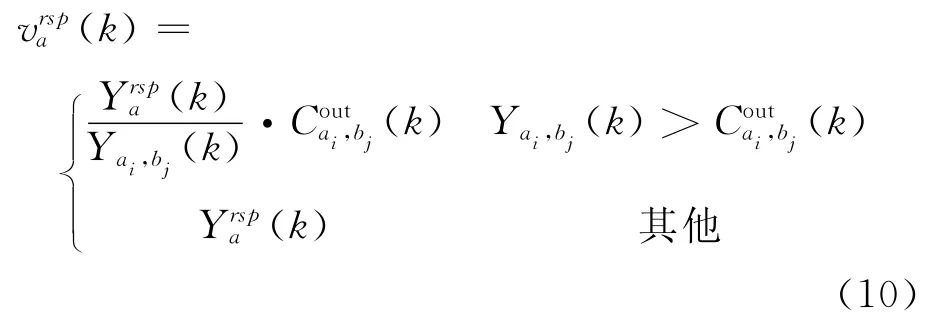
节点流量守恒公式表示如下.
式中:frsp*(k)为在间隔数k的起点路段中,实际路径出口流量.起点路段的实际路径出口流量是在点排队假设下,根据下游路段可接受流量和路径入口流量frsp(k)得到.
1.3 路段行程时间
基于FIFO原则,路段转向行程时间可以通过下式计算
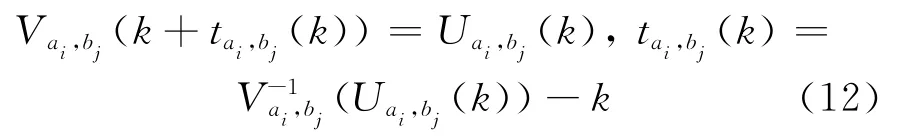
1.4 起点终点流量模拟
先前在破坏排队条件下对起点和终点流量的模拟都假设,起点和终点都出现在没有输入路段和输出路段的节点处,这种假设使破坏排队条件下的路网并没有普遍性.本文在其基础上放松了相应的假设条件,给出了一种新的模拟方法.
1)如果一个节点即是交通节点,又是起点或终点,则可以作一个连接此节点的虚拟起点(终点)路段.此路段有一个恒定的出口容量,所有通过虚拟起点(终点)进入(退出)路网的车辆都要受到虚拟路段出口容量以及相应的下游(上游)路段容量的限制.
2)当一个节点是多个OD对的起点(或终点)时,则共用一个节点的起点(或终点)OD对只设置一个虚拟路段.
3)所有虚拟的起点(或终点)路段的流量都通过点排队原则模拟.
2 仿 真
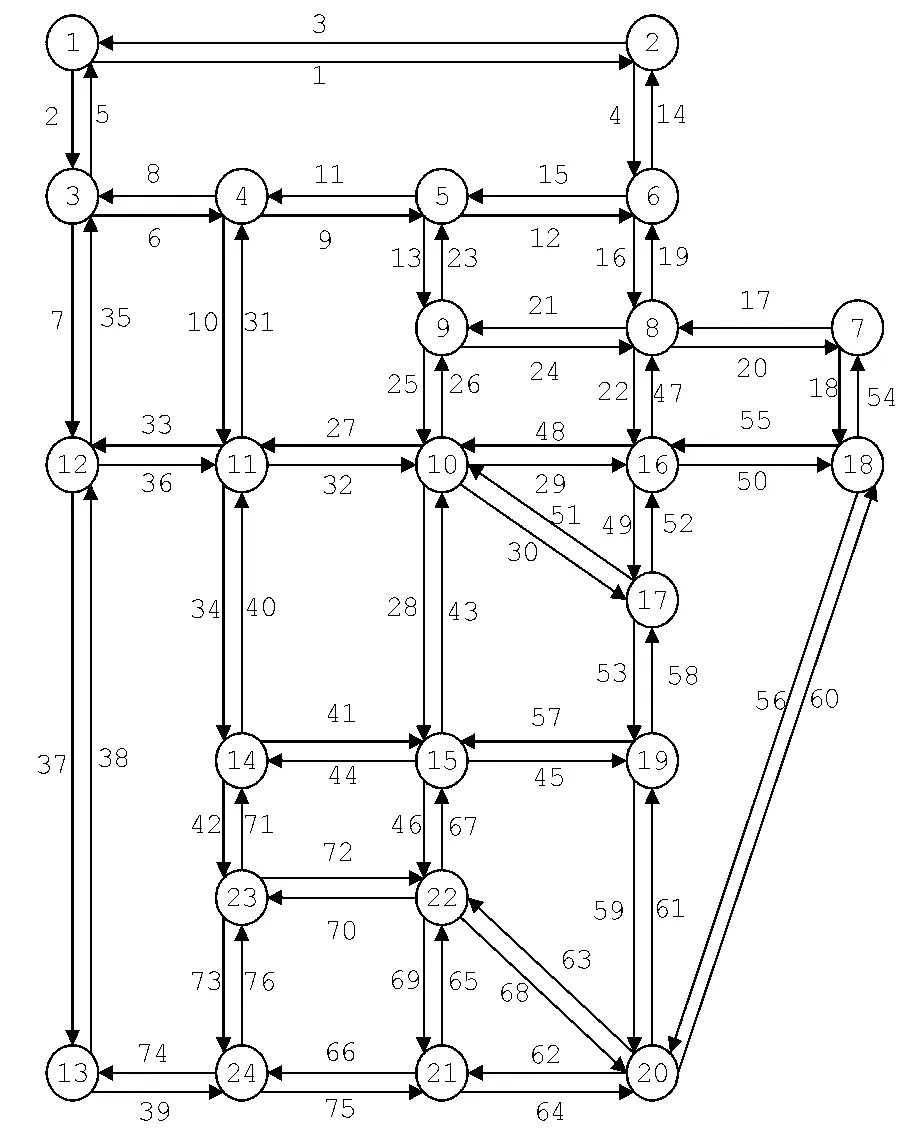
图1 Sioux Falls路网
试验路网见图1,包括76个路段,4个OD对,(1,20)之间有7条路径,(1,13)之间有1条路径,(6,13)之间有4条路径,(4,20)之间有7条路径,共19条路径.每个路段的前向波速度为50km/h,后向波速度为25km/h,路段长度是随机产生的,路段拥挤密度是200veh/km,路段2的入口容量为3 000veh/h,出口容量为3 000 veh/km,路段37的入口容量为1000veh/h,出口容量为1 000veh/km,其它路段的入口容量为1 500veh/h,出口容量为1 500veh/km.时间间隔长度设为0.01h.
图2给出了在路段2上转向路段37和路段6的出入口流量率,由于路段37的出入口容量较小,因此在路段2上转向路段37的流量首先处于拥挤状态,而转向路段6的流量并没有立刻处于拥挤状态,而随着时间的推移,两个转向流量都逐步处于拥挤状态;这也验证了先前的节点分流模型的思路,在一个路段上由于不同的转向流量率的限制,路段上呈现不同的拥挤状态,而不是如先前的一些模型,认为路段只有一种流量状态,也可以认为这种模型在一定程度上给出了更加真实的结果.图3给出了在路段2上转向路段37和路段6的行程时间,从图中可以看出由于转向容量的不同,在同时进入路段2的车辆在路段上的行驶时间的差异.在图4中给出了路段1的入口和出口流量状态,由于路段1只有一个下游和上游路段,从图中可以看出路段1的出口流量非常好的跟踪了入口流量,也就是说在路段处于非拥挤状态时,本文给出的模型能较好地反映路段流量的传播过程.
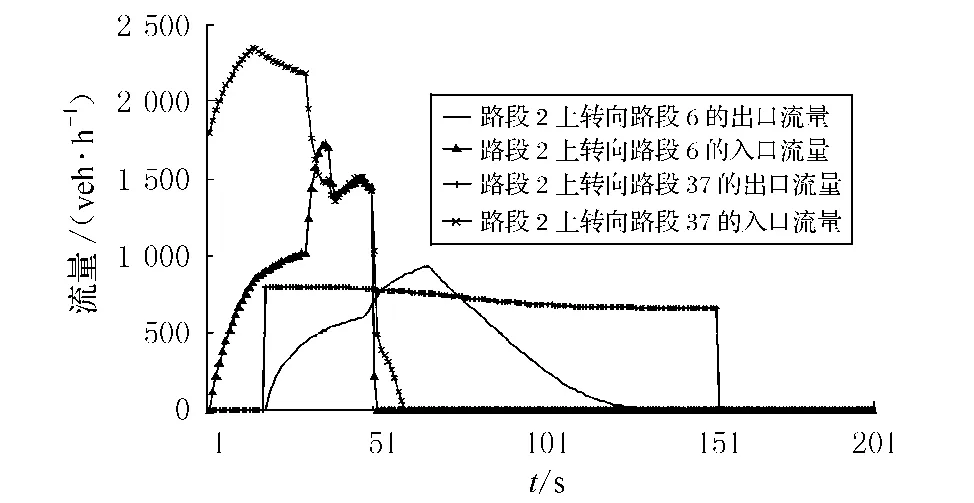
图2 路段2的流量状态

图3 路段2的行程时间
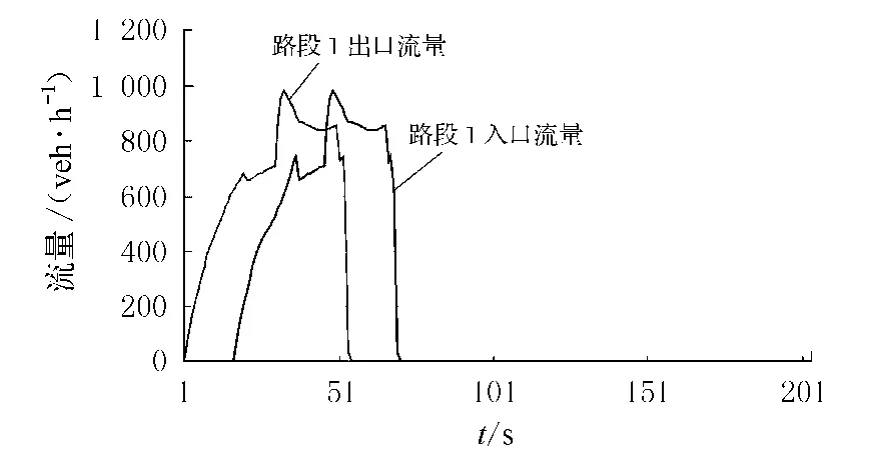
图4 路段1的流量状态
3 结束语
本文建立了一个基于转向容量和破坏排队的动态网络装载模型.模型考虑了在一个路段上由于下游分流路段可接收流量的不同进而导致上游路段出现不同的拥挤状态,也就是说,一个路段上可以出现不同的排队状况,进而以Newell提出的简单动力波理论为基础,认为路段只有2种波形存在:前向波和拥挤波.在一个中等规模的路网中进行仿真试验表明,模型不但能够模拟一个路段上的不同排队状况,同时也可以很好模拟非拥挤状况下的流量转播状况.
[1]李曙光,周庆华.基于GIS的多模式动态网络装载程序设计研究[J].公路交通科技,2006,23(9):81-84.
[2]Wu J H,Chen Y,Florian M.The continuous dynamic network loading problem:a mathematical for-mulation and solution method[J].Transportations Research B,1998,32(3):172-187.
[3]Xu Y W,Wu J H,Florian M.Advances in the continuous dynamic network loading problem[J].Transportation Science,33(2):341-353.
[4]Rubio-Ardanaz J M,Wu J H,Florian M.Two improved numerical algorithms for the continuous dynamic network loading problem[J].Transportation Research Part B,2003,37(3):171-190.
[5]Daganzo C F.The cell transmission model,part II:network traffic[J].Transportation Research B,1995,29(5):79-93.
[6]Newell G F.A simplified theory of kinematic waves in highway traffic,part I:general theory;part II:queuing at freeway bottlenecks;part III:multi-destination flows[J].Transportation Research B,1993,27(2):281-313.
[7]Kuwahara M,Akamatsu T.Dynamic user optimal assignment with physical queues for a many-to-many OD pattern[J].Transportation Research Part B,1993,27(3):461-479.
[8]Daiheng Ni.Extension and generalization of newell's simplified theory of kinewave[D].Atlanta:Georgia Institute of Technology,Doctor paper,2004.
[9]Li S,Xu H.Physical-queue discrete-time dynamic network loading with multiple vehicle types[J].Journal of Transportation Systems Engineering and Information Technology,2009,9(1):56-61.
[10]Bliemer M C J.Dynamic queuing and spillback in analytical multiclass dynamic network loading model[J].Transportation Research Record,2007,2029(1):14-21.

