基于应变梯度的微切削第一变形区几何分析模型的研究*
吴继华 刘战强
(绍兴文理学院工学院1) 绍兴 312000) (山东大学机械工程学院2) 济南 250061)
微切削加工技术在微细产品的加工中广泛应用.与其他微细加工技术(如微刻蚀、激光、电解等)相比,微切削具有如下优点:(1)加工材料范围广泛;(2)三维加工能力强;(3)加工尺度微小;(4)加工精度高.研究微切削过程中的变形机理对于控制加工过程,提高加工质量,降低加工成本具有重要意义.
剪切区模型广泛应用于宏观切削理论的研究,如用于求得应变率,描述切削过程参数及预测加工结果.准确的剪切区形状参数直接影响到应变率等切削过程参数计算的精度.切削过程中第一变形区高应变、高应变率、高温度的剧烈变形环境使第一变形区几何参数的测量变得非常困难.常规的方法是用录像机录制切削过程,再用测量装置获得剪切区的厚度和长度[1],但因实验操作过程复杂且高速切削下采集的图像模糊,使得测量数据易产生误差.目前未曾有文献涉及到应用分析法对第一变形区进行理论建模并给出几何尺寸预测模型.
在宏观弹塑性理论中,未引入内禀特征长度,无法预测切削用量在微米级微切削过程的变形[2].应变梯度塑性理论将塑性应变的二阶空间梯度引入到屈服函数中,包含内禀特征长度以描述微观尺度下的变形特性.
本文基于应变梯度构建了微切削的力学模型,提出第一变形区几何尺寸的分析预测方法,并用正交切削实验验证了模型的有效性.
1 理论分析
1.1 第一变形区厚度的确定
应用弹塑性力学理论建模正交切削过程.正交切削过程中因为工件受二维切削力作用,故认为正交切削过程是平面应变状态.工件受到切削力和进给力的熨压和剪切作用及摩擦力的剪切作用,产生二向正应力和剪切应力.第一变形区是变形剧烈的区域,应变可达1~10,应变率可达105~106s-1[3],可以把切削过程中的第一变形区等效为受熨压和剪切作用而产生的绝热剪切带,绝热剪切带的倾角就是剪切角.图1为G.Sutter在正交切削实验中得到的切削过图像[4].图中标示的矩形区待加工工件受力情况反映为图2.图2中t为切削厚度(正交切削中为进给量);φ为剪切角;w为第一变形区的厚度;L为第一变形区的长度.

图1 实际微切削过程图像
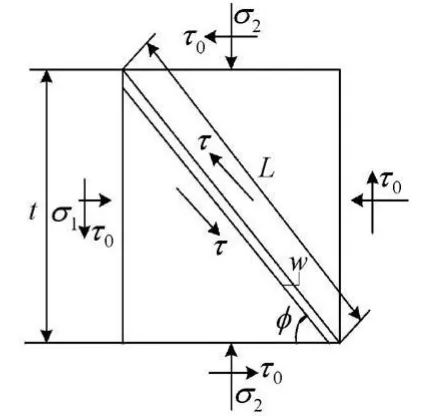
图2 正交切削过程力学模型
应变梯度模型可由连续介质非局部模型通过泰勒级数展开获得,通过选择适当的非局部权函数,仅保留级数的前二项,可表示为
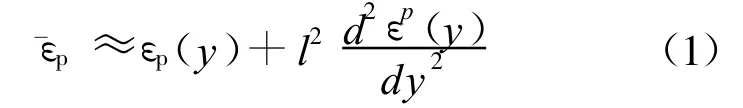
剪切应力与剪切应变的关系为

式中:k为与材料有关的系数;n为材料的硬化指数.考虑到剪切应变εp是坐标y的函数,利用弹性区和剪切塑性区的交界处的边界条件,当y=时
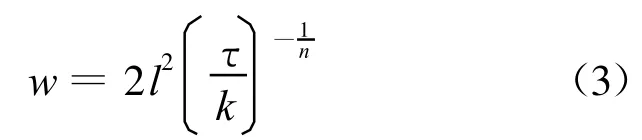
从式(3)可见,第一变形区的厚度不仅与材料的内禀特征长度有关,还与外加剪切应力τ及硬化系数k有关.材料的内禀长度l越小,即材料相对比较均匀时,第一变形区厚度越小.
1.2 剪切应力τ的求解
由材料力学可得

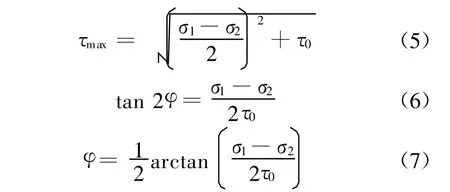
设第一变形区的长度为L,由图2可得,

由式(9)得,当切削厚度越大时,第一变形区的长度越大.
2 正交切削实验验证
为了验证模型的正确性,正交切削实验在精密车削中心PUMA 200M上进行,不加冷却液.方案如图3所示.采用肯纳公司的超细晶粒硬质合金刀具,使切削刃宽度大于待切削工件的宽度,以消除刀尖半径的影响.工件选用生产中普遍使用的45#钢,实验参数如表1所列.实验采用瑞典生产的Kislter车削测力仪测得正交微切削过程中的切削力,可以准确地获得水平分力FH(主切削力Fc)和垂直分力FV(进给力Ff).

图3 正交切削实验方案
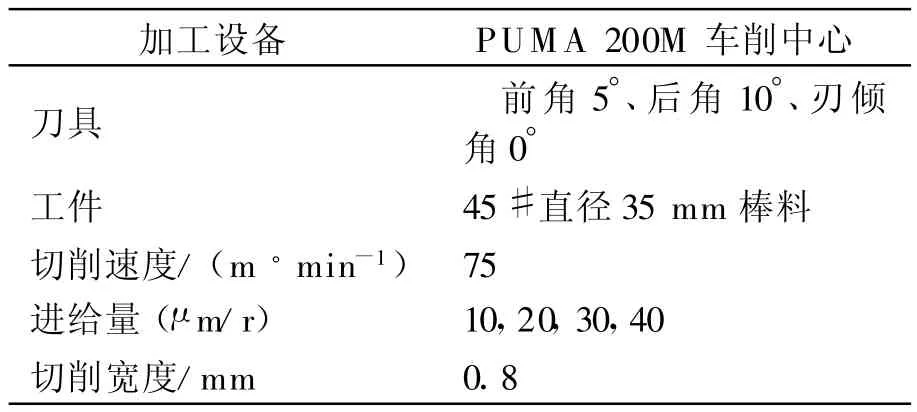
表1 切削参数
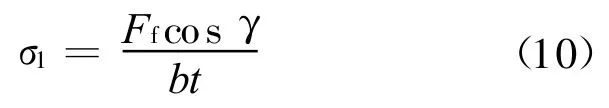
式中:b为背吃刀量;t为进给量;γ为刀具前角.
σ2可由下式计算

τ0由摩擦力产生,由下式计算
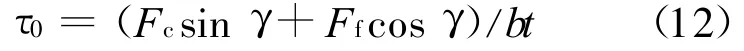
内禀特征长度l可以通过在该尺度范围内的各种材料实验来测定.将以上公式代入式(3)和式(9)求得第一变形区的厚度和长度.微切削中第一变形区的尺寸与进给量的关系如图4所示.

图4 第一变形区尺寸与进给量的关系
由图4可见,随着进给量的增大,第一变形区厚度反而减小而第一变形区的长度增大.
3 结束语
用应变梯度塑性理论确定了第一变形区的长度和厚度,构建了包含内禀材料特征长度的微切削中第一变形区的力学模型,并用实验验证了模型的可靠性,为微切削过程中变形参数的求得和切削结果的预测提供了很好的思路.任何解释都是在人为给定的边界条件下进行的,都与实际材料中的情况有一定的差距.因微切削过程中产生的热量很少,故文章未考虑切削热对应力、应变及第一变形区几何模型的影响.如何完善微切削模型,使理论更好的反映实际情况是今后微切削理论研究发展的方向.
[1]陈日曜.金属切削原理[M].北京:机械工业出版社,2002.
[2]Zhang H,Alpas A T.Quantitative evaluation of plastic strain gradients generated during orthogonal cutting of an aluminum alloy[J].M aterials Science and Engineering.2002,A332:249-254.
[3]Pujanaa J,Arrazolaa P J,Saoubi R M.Analysis of the inverse identification of constitutive equations applied in orthogonal cutting process[J].International Journal of Machine Tools&M anufacture.2007,47:2153-2161.
[4]Sutter G.Chip geometries during high-speed machining for orthogonal cutting conditions[J].International Journal of Machine Tools&M anufacture. 2005,45:719-726.

