预制钢筋混凝土结构在地震荷载下的往复荷载分析

李运升 陈红鸟

(中国地质大学(武汉)工程学院 武汉 430074)

根据现有规范设计的钢筋混凝土结构,在地震作用下会有较大的变形,甚至是消耗大量能量的塑性滞回变形.塑性变形只集中发生在结构受力和变形显著的部位,即结构的关键区域.为研究结构在静态往复荷载下的非线性反应,需集中研究结构关键区域的滞回变形行为.

数值模拟方法是研究结构在往复荷载作用下滞回变形的有效手段,而建立真实反映结构滞回反应机理的材料非线性模型是数值模拟的关键.数值模拟既要仿真结构的真实性,又要简单,便于数值计算,需要消耗大量时间才能完成计算的数字模型是不理想的.数值模型建立之后,要对结构发生塑性变形的关键区域进行判断.大量的钢筋混凝土结构试验和研究表明,在较大的往复荷载作用下,钢筋混凝土构件端部的受力和变形较大,因此关键区域一般出现在构件的端部.

Filippou及其同事提出钢筋混凝土结构在往复荷载下,其关键区域构件刚度的降低是影响结构滞回变形的主要因素[1-2].结构刚度的降低会引发以下效应：(1)在承受较大的周期往复荷载时,结构中未损坏部分的柔度和自振周期会升高;(2)结构的整体耗能性能降低;(3)结构的内力会重新分布从而使得一些区域有过度的变形.结构因地震荷载而产生的内力和变形对结构的柔度、自振周期、耗能性能非常敏感,因此结构刚度的降低将影响到整个结构的抗震性能.

本研究对前面模拟的数值模型进行修改,选用合适的滞回变形模型,对单层预制钢筋混凝土结构在周期往复荷载下的非线性静态反应做出预测,从而检验试验数据和数值模型的可靠性.

1 试验模型的建立

在试验研究中,根据欧洲规范8中的抗震设计要求建立试验模型,并对试验模型施加强度不同的地震荷载,记录其受力和变形情况.模型由6根柱子、梁、双T形屋面板构成,柱子从基础延伸出来,高5 m.在模型中,有两跨长8 m的梁和一跨长8 m的屋面板,施加的地震荷载方向与屋面板平行,见图1.模型的俯视图和地震荷载方向见图2.

图1 试验模型

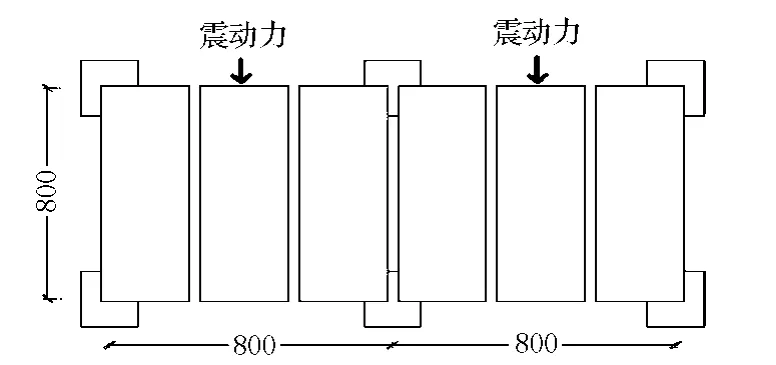
图2 模型的俯视图/cm

在类动态试验中,输入的地震波来自意大利Tolmezzo于1976年记录的地震加速度图,根据欧洲规范8中弹性设计规范对该加速度现场效应进行过滤,修改后的地震波见图3[3-4].

图3 地震加速度(Tomezzo 1976)

2 数值模拟过程和结果

结构的塑性变形集中在柱子的底端,如图4所示.在试验中,周期往复荷载的加载历史见图5.周期往复荷载的振幅是依据单层结构屋顶在钢筋屈服时的水平位移δy选定的.δy=80 mm,每个振幅值循环三个周期之后以δy/2=40 mm的振幅递增.每个振幅值循环3个周期,是为了测定结构变形的稳定性.

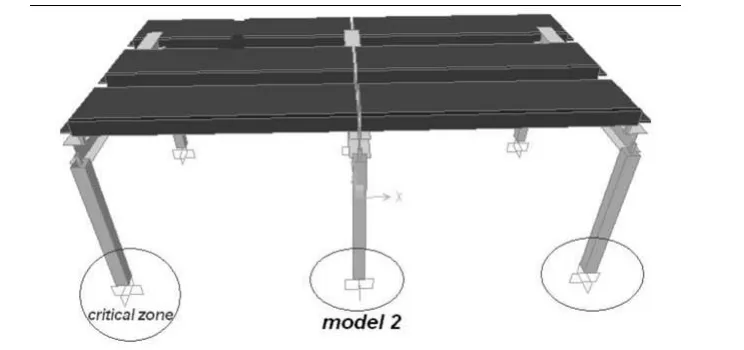
图4 塑性变形集中的区域

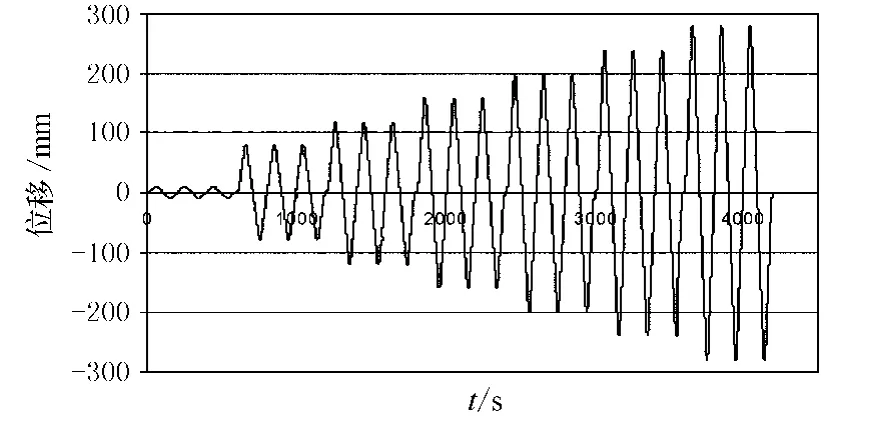
图5 周期往复荷载的加载历史

周期往复荷载分析不是SAP2000程序自带的分析类型,采用两种方法来实现这种往复加载分析.第一种方法是使用时程分析法,对控制点施加合适的约束,并把往复加载历史简化为地震荷载施加于控制点上.这种方法思路比较直接,但是模型复杂,不易控制;第二种方法就是把往复加载历史简化为一系列首位相接的推覆分析,每步分析都在前一步分析的基础上进行,尽管步骤繁多,但是模型简单,容易控制.第二种分析方法的基本原理就是推覆分析,因此本节将重点介绍该模拟方法的结果.

结构的材料非线性和前两个分析中用到的一样,也是取决于构件材料的力学和截面性质,由柱子底部的弯矩-转角关系.滞回变形模型的选用与时程分析相同,先采用 Takeda模型,后又采用Pivot模型[5-7].采用Takeda滞回变形模型,结果如下：考虑不同的塑性铰长度lp=0.55 m(通过经验公式计算得到),0.4 m(柱子截面的高度h), 0.2 m(柱子截面高度的1/2),推覆分析的结果与试验滞回曲线的比较见图6.

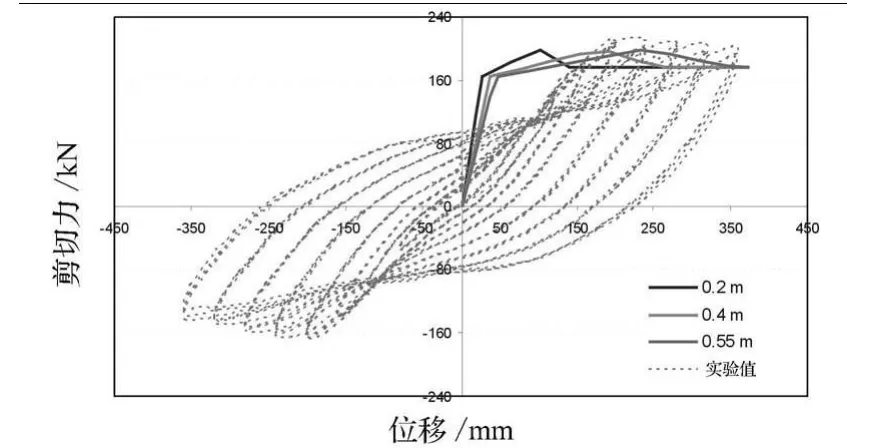
图6 不同塑性铰长度的性能曲线与试验滞回曲线

分析图6发现,当塑性铰长度lp=0.55 m时,数字结果与试验数据更为接近,因此应当选用0.55 m的塑性铰长度.

图7 数字模拟的性能曲线与滞回曲线

从图7可以看出,在数值模拟中,推覆分析的性能曲线就是滞回曲线的包络线.掌握这一规律之后,不需要每次都求出滞回曲线来判断剪力和位置大小,为参数的评估和选用节约大量时间.数值模拟的结果与试验的比较见图8和图9.

结果表明,Takeda模型可以模拟结构在水平往复荷载下的滞回变形行为,但是结构的刚度只在加载过程中有衰减,卸载的刚度保持不变,与实际不符.

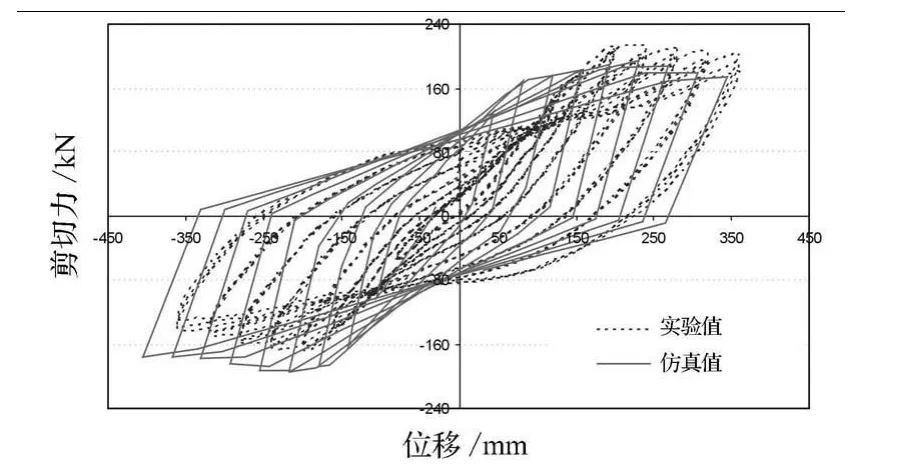
图8 数值模拟曲线与试验滞回曲线

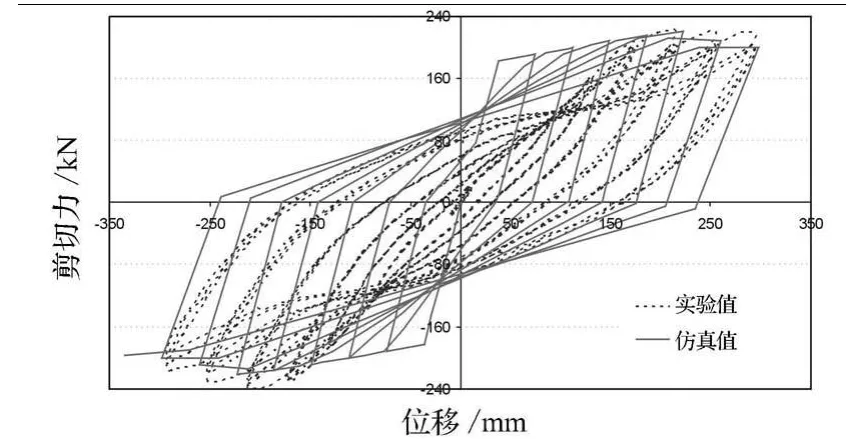
图9 数值模拟曲线与试验滞回曲线

为了模拟结构在加载和卸载过程中刚度均有衰减的特性,采用Pivot滞回变形模型.数值模拟结果与试验的对比见图10和图11.

图10 数值模拟曲线与试验滞回曲线

图11 数值模拟曲线与试验滞回曲线

结果表明,Pivot模型不仅可以很好地反映结构的滞回变形行为,还具备较好的刚度衰减规律,与试验数据比较接近.用同样的方法检验结构的局部反应,主要由非线性连接处的弯矩-曲率关系表示,见图12和图13.

3 结 论

1)模拟结果和试验数据的吻合程度较好,用Takeda模型和Pivot模型都可以在一定程度上再现试验过程.

图12 数值模拟曲线与试验滞回曲线

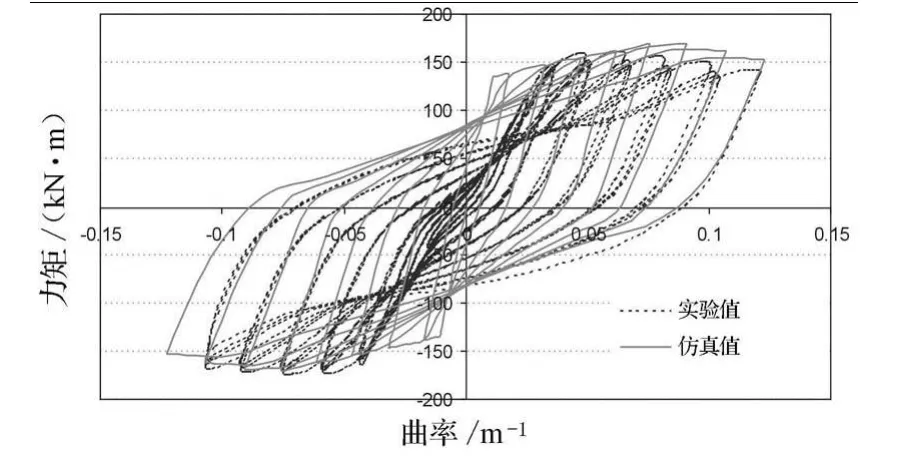
图13 数值模拟曲线与试验滞回曲线

2)因为试验模拟在前面所作的类-动态试验中已经受到损坏,所以刚度降低;在数值模拟中,结构的刚度降低不明显,原因取决于SAP模型不能保存结构被损坏的情况.

3)在数值模拟中,结构的刚度衰减并不明显,而试验模型的刚度有很明显的降低.从对结构刚度衰减的模拟看,Pivot比Takeda模型更适合做往复荷载分析.

4)虽然Pivot模型可以比较可靠地预测结构在往复荷载下的反应,但是对Pivot参数的选用必须谨慎.大量的尝试和分析发现,在时程分析中,α和β值取较小为宜,因为结构遭受的损坏不显著,刚度没有明显降低;往复荷载分析中类-动态试验之后,结构内部的损伤较大,应该选用较大的α和β值.

致谢：该研究是在米兰理工大学提供的“ICE-Unioncamere Scholarships”奖学金的支持下进行的,本文的试验数据由欧洲研究课题组提供,在此表示感谢.

[1]Ferrara L,Mola E,Negro P,Toniolo G.Seismic behavior of RC precast frame buildings：design,scope and lessons of a state-of-art experimental investigation[R].2007.

[2]Filip C,Filippou,D＇Ambrisi A,Issa A.Nonlinear static and dynamic analysis of reinforced concrete subassemblages[R].No.UCB/EERC-92/08,Earthquake Engineering Research Center College of Engineering University of California,Berkeley,1992.

[3]Domingues Costa J L,Bento R,Levtchitch V,Nielsen M P.Simplified non-lineartime-history analysis based on the Theory of Plasticity[C]//Brebbia C A. Earthquake Resistant Engineering Structures V,UK, Ashurst Lodge：WIT Press,2006.

[4] Clough R W,Benuska K L,Wilson E L.Inelastic earthquake response of tall buildings[C]//Proceedings Third World Conference on Earthquake Engineering,New Zealand,New Zealand National Committee on Earthquake Engineering,1965.

[5]叶列平,陆新征,马千里,汪训流,缪志伟.混凝土结构非线性分析模型、方法及算例[J].工程力学, 2006,23(2)：131-140.

[6]李国强,沈祖炎.钢框架弹塑性静动力反应的非线性分析模型[J].建筑结构学报,1990,11(2)：51-59.

[7]Takeda T,Sozen M A,Nielsen N N.Reinforced concrete response to simulated earthquakes[J].Journal of the Structural Division,ASCE,1970,96(12)：2 557-2 573.