基于模糊神经网络的信息系统安全风险评估研究＊

王甲生 付 钰 吴晓平

(海军工程大学信息安全系 武汉 430033)

针对信息系统的安全风险评估问题,国内外学者运用模糊数学理论、灰色系统理论、粗糙集理论、贝叶斯网络等建立了风险评估模型,取得了很多研究成果[1-5].这些研究成果是对信息系统安全风险评估理论的发展和完善,但还没形成系统的评估方法体系.本文在对信息系统的安全风险进行详细分析的基础上,采用基于改进模糊AHP的模糊综合评判法来对信息系统中边界不清、只能用模糊的非定量的语言来描述的风险因素进行定量化分析.在风险量化过程中引入人工神经网络的智能控制算法,利用其强大的自适应能力与非线性映射能力,降低了评估过程中的人为因素,较好的保证了评估结果的客观性.

1 信息系统安全风险评估模型

根据《中华人民共和国计算机信息系统安全保护条例》中的定义,信息系统是指由计算机及其相关的和配套的设备、设施(含网络)构成的,按照一定的应用目标和规则对信息进行采集、加工、存储、传输、检索等处理的人机系统[6].

信息系统的安全风险涉及物理安全、逻辑安全以及安全管理等多个方面,根据 ISO/IEC 15408和信息技术安全通用要求(GJB5095-2002),本文将从物理安全、运行安全、应用安全和安全管理4个层面对信息系统进行安全风险评估,信息系统安全风险评估的层次结构模型如图1所示.

其中,物理安全是保证信息系统安全的基本前提,其目的是保证系统所处环境、系统设备以及介质(媒体)的安全性;运行安全是信息系统各项业务顺利开展的必要条件,其着眼于信息系统的业务持续性;应用安全是信息系统安全的重要方面,其目的通过采用各种信息安全技术,保证信息系统各项应用的安全;安全管理是信息系统安全的灵魂,其目的是建立科学规范的安全管理体系,为信息系统的安全管理提供保障.

2 基于模糊神经网络的信息系统安全风险评估

2.1 信息系统安全的多级模糊综合评判

在应用模糊综合评判法对系统进行风险评估时,各风险因素的权重分配是一个关键问题.传统AHP在对风险因素的相对重要性赋值时没有考虑到专家判断的模糊性和不确定性,且存在诸如判断一致性与矩阵一致性的差异、一致性检验的困难以及缺乏科学依据等问题[7].针对这些问题,本文提出了改进的模糊AHP,引入模糊一致判断矩阵来表示信息系统各层次风险因素的相对重要性,给出了一种模糊一致判断矩阵的排序方法,以求得各风险因素的权重,在此基础上运用模糊综合评判法来对信息系统的安全风险进行综合评估.

图1 信息系统安全风险评估的层次结构模型

模糊一致矩阵的以上性质反映了人们决策思维的习惯,其合理性解释如下：(1)是元素i与j相对重要性的度量,且越大,元素i比j越重要,表示i比j重要;反之,表示j比i重要表示元素与其自身相比较是同等重要的;(2)表示元素i比j重要的隶属度,那么表示i不比j重要的隶属度,即j比i重要的隶属度,即是模糊互补矩阵;(3)模糊一致矩阵具有很好的鲁棒性;(4)如果元素i比j重要,且元素j比k重要,那么元素i一定比元素k重要;反之,如果元素i不比j重要,且元素j不比k重要,那么元素i一定不比元素k重要.

在专家进行模糊判断的时候,构造的判断矩阵通常是模糊互补矩阵,由模糊互补矩阵构造模糊一致矩阵的方法如下.

对模糊互补矩阵R=(fij)n×n按行求和,记为ri,1=1,2…,n,对其进行以下数学变换则由此建立的矩阵是模糊一致矩阵.

模糊一致矩阵排序的方法如下,其合理性和正确性已经在文献[8]中给出了证明.

若矩阵R=(rij)n×n是模糊一致矩阵,则其排序值可由下式计算

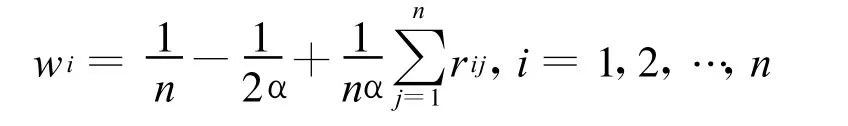
式中：α满足α≥(n-1)/2,且当α越大时,权重之间的差异越小;α越小,权重之间的差异则越大;通过调整参数α的大小,对权重结果的灵敏度进行分析,从而有助于专家做出正确的权重判断.

2.2 信息系统安全的人工神经网络模型

神经网络[9](back propagation,BP),多层前馈式误差反传播神经网络是目前应用最为广泛和成功的神经网络之一.BP神经网络的具体学习过程见文献[9].通过BP神经网络的迭代算法,可使网络输出与训练样本总体的实际值的均方误差降低到满意的程度,从而获得稳定的网络结构和连接权值,然后就可对未知样本进行识别预测,从而获得信息系统安全风险的量化值.

2.3 基于模糊神经网络的信息系统安全风险评估模型

本文在已提出的基于改进的模糊AHP的多级模糊综合评判的基础上,引入BP神经网络,提出基于模糊神经网络(FNN)的信息系统安全风险评估模型.基于FNN的信息系统安全风险评估模型如图2所示.

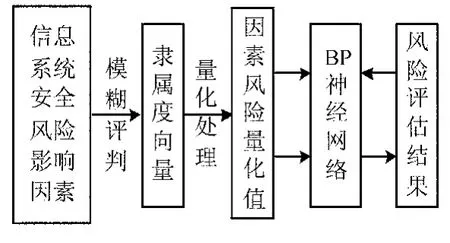
图2 基于FNN的信息系统安全风险评估模型

同时,为了提高BP网络的泛化能力,采用初期终止[10]的方法,将收集到的可用样本随机的分为两个部分,一部分作为训练集,另一部分作为测试集,其中训练集用于计算网络性能函数的梯度和更新后的网络权值,测试集用来检验神经网络的训练结果.在训练时将训练和测试交替进行,直到训练误差和测试误差都下降到一个较小值.

基于FNN的信息系统安全风险评估,主要包括以下三个步骤.

步骤1 训练样本集的设计 设风险因素i对评判集的隶属度向量为ri;β为各风险等级的赋值向量,那么该风险因素的风险量化值为：xi= ri°βT.

设系统多级模糊综合评判的结果为B,那么该系统安全风险的综合评分值为：p=B×βT.

步骤2 BP网络结构的设计 在评估模型的网络结构中,输入层节点数即风险因素的数量,输出层节点为一个.对于隐含层的数量和各隐含层的节点数量,已经证明,包含一个隐含层的三层神经网络,只要隐含层节点数足够多,就能以任一精度逼近有界区域上的任意连续函数.因此,为简化评估模型的结构,提高模型训练效率,本文采用三层的BP神经网络构建信息系统安全风险评估模型.隐含层节点的数目根据文献[9]中提出的几个经验公式,利用试凑法,通过仿真实验来确定.

步骤3 BP神经网络的训练和测试 在实际应用中,BP网络学习算法存在学习收敛速度缓慢、目标函数容易陷入局部极小值而无法得到全局最优解的问题.针对这些问题,本文采用基于Levenberg-Marquardt法的改进算法,相对于其他的改进算法,该算法具有收敛速度快、精确度高、迭代次数少的特点.

3 实例分析

设计一个三层的BP神经网络.输入层有23个节点,对应的输入为上述23个风险因素的风险量化值;输出层有1个节点,对应的输出为系统安全风险的综合评分值;根据文献[9]中的经验公式,隐含层的节点数设为个.输入层到隐含层以及隐含层到输出层之间的传递函数采用对数Sigmoid函数,即在Sigmoid函数作用前对输入数据预处理.网络的训练函数采用trainlm()函数,对应于采用Levenberg-Marquardt法的改进算法.性能函数采用均方误差性能函数mse(),并设定e=0.000 1,网络学习速率设为α=0.05.

为了保证网络训练的精度以及网络的性能,选用了其中比较具有代表性的30个样本作为训练样本集.同时,为了提高网络的泛化能力,采用初期终止的方法,将30个样本分为2个集合：27个样本作为训练集,3个样本作为测试集.

训练集和测试集样本通过模糊综合评判法得到的安全风险评估结果与通过人工神经网络得到的训练结果分别如表1和表2所列.

BP神经网络对训练集样本的误差输出和训练次数如图3所示,其中横坐标表示网络的训练次数,纵坐标表示BP神经网络的误差精度.

表1 训练集样本的模糊综合评判结果与模糊神经网络训练结果

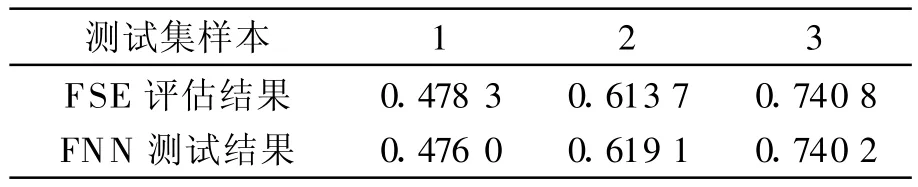
表2 测试集样本的模糊综合评判结果与模糊神经网络测试结果

图3 神经网络的输出误差和训练次数

由图3可知,网络在经过8～9次训练后,输出误差即达到了设定的精度e=0.000 1.

训练样本集的绝对输出误差如图4所示,其中横坐标表示1～30个样本,纵坐标表示各样本的样本输出值与训练输出值的绝对偏差.

图4 训练样本集的绝对输出误差

由图4可知,训练样本集的绝对输出误差在10-4～8.2×10-3之间,相对输出误差在0.02%～1.22%之间,完全满足精度需要.

模糊综合评判结果与模糊神经网络输出结果的比较见图5,其中横坐标表示1～30组样本,纵坐标为两种方法的安全风险评估输出值.

图5 模糊综合评判结果和模糊神经网络输出结果比较

由图5可知,两种方法的输出结果具有非常好的一致性,两条线几乎重合,相关系数达到R= 0.998.这说明,基于模糊神经网络的信息系统安全风险评估方法的输出结果能以较高精度逼近由多级模糊综合评判法得到的评估结果.两者之间的差异在一定程度上反映了模糊神经网络对不同专家意见的综合和各风险要素与信息系统安全之间的复杂关系,且表明模糊神经网络具有较强的自适应能力,该模型可以满足实际的应用需要.

4 结束语

在对信息系统安全风险的特性进行了详细分析的基础上,提出了一种结合多级模糊综合评判与人工神经网络的风险评估方法.多级模糊综合评判法中权重集的构建采用改进的模糊AHP,使得权重的计算更为合理;通过引入人工神经网络的智能控制算法,减少了评判过程中的随机性和专家主观上的不确定性,并在一定程度上缩小了专家主观判断的差异,使得评估结果更加科学合理.实例分析表明,该方法可行有效,为信息系统安全风险评估提供了一种有效途径.

[1]赵俊阁,张 琪,付 钰.贝叶斯网络在信息安全风险评估中的应用[J].海军工程大学学报,2007(6)：67-70.

[2]付 钰,吴晓平,严承华.基于贝叶斯网络的信息安全风险评估方法研究[J].武汉大学学报：理学版, 2006(5)：631-634.

[3]陈 錬,文巨峰,韩冰青.信息系统安全风险评估[J].计算机工程与应用,2006(4)：145-148.

[4]Jhm T,Carr V.A proposal for construction project risk assessment using fuzzy logic[J].Construction Management and Economics,2000,18(4)：491-500.

[5] Pawlak Z.Rough sets and intelligent data analysis [J].Information Sciences,2002,14(7)：1-12.

[6]方 勇,刘嘉勇.信息系统安全理论与技术[M].北京：高等教育出版社,2008.

[7]吴晓平,汪 玉.舰载装备系统综合评估的理论与方法[M].北京：科学出版社,2007.

[8]张吉军.模糊一致判断矩阵3种排序方法的比较研究[J].系统工程与电子技术,2003,25(11)：1 370-1 372.

[9]张德丰.M ATLAB神经网络应用设计[M].北京：机械工业出版社,2009.

[10]肖 龙,方 勇,戴宗坤.基于模糊神经网络的信息系统风险分析[J].计算机应用研究.2006,(5)：137-139.