钢筋混凝土桥梁结构耐久性的评估方法研究

徐 斌（江苏润扬交通工程集团有限公司，江苏 扬州225003）

1 绪论

随着我国经济的飞速发展，各地均大量修建了以钢筋混凝土结构为基础的桥梁，随着这些桥梁的使用，由于混凝土结构的耐久性病害而导致的经济损失是巨大的，并且耐久性问题会越来越严重。

混凝土结构耐久性是基于材料耐久性的进一步深化。混凝土结构在自然环境和使用条件下，随着时间的推移，材料逐渐老化和结构性能劣化，出现损伤甚至损坏，这是一个不可逆过程。它不是直接由力学因素引起的。首先是混凝土材料的物理化学作用的结果，继而影响到建筑物的使用功能和结构的承载力下降，最终会影响整个结构的安全。我国既有以混凝土为主体的结构在数量上居多，所以混凝土结构耐久性问题就显得更加突出。受地理、气候环境影响，存在着“南锈北冻”的耐久性破坏特征。华北地区气候严寒，混凝土结构往往表现为冻融破坏；而我国南方地区，气候普遍湿热，常受海洋环境的影响，往往导致混凝土碳化和氯离子侵蚀，从而引起钢筋锈蚀。

本文主要内容是从整体上运用模糊数学理论研究既有钢筋混凝土桥梁结构的耐久性评估，预测结构的剩余使用寿命，并且比较好地实现耐久性评估和剩余使用寿命预测的结合。

2 钢筋混凝土桥梁结构耐久性的评估方法

既有钢筋混凝土桥梁结构耐久性评估方法[8]是伴随着建筑结构可靠性评估理论发展起来的。传统的既有桥梁结构耐久性评估主要是应用层次分析法，将影响桥梁耐久性的因素层次化，形成一个多层的、每层包含若干组影响因素的体系，在影响因素体系建立之后，一般采用专家意见调查确定各层次各影响因素的权重。有了整座桥梁的耐久性评估体系及各层影响因素的权重，再通过各种检测手段确定底层各影响因素的状态，应用综合性评估方法(基于设计规范的方法、专家经验评定法、可靠度理论等)计算出其他各层影响因素的状态，最后得到一个表示桥梁耐久性的综合损伤值。

以往通常使用的钢筋混凝土桥梁结构耐久性的评估方法有：1）外观调查评估法2）专家经验评估法3）基于设计规范的方法4）现场荷载试验法5）层次分析法6）基于可靠度理论的方法。

由于影响既有桥梁结构耐久性的因素很多而且包含了大量的不确定性，因此传统的既有桥梁结构耐久性评估方法在某种程度上并不能给出确切结论，不能很好的满足实际评估需要。

近几年来，在模糊理论基础上逐步发展起来的各种既有桥梁结构耐久性评估技术可以弥补以上不足，扩大了既有桥梁结构耐久性评估工作的内涵及外延。可以说应用模糊理论技术的既有桥梁结构耐久性评估技术是新一代既有桥梁结构耐久性评估系统的发展趋势。

3 钢筋混凝土桥梁结构耐久性的模糊综合评估

自从可靠度引入土木工程以来，许多学者一直在探索如何运用可靠度来评估结构的耐久性，发展了以传统的概率统计为基础的可靠性理论。运用这些方法对结构耐久性进行评估是比较理想的，但在具体评估结构的耐久性问题时，不仅由于体系可靠度理论的不成熟，并且在如何界定耐久性极限状态和耐久性失效方面存在很大的争议。

模糊数学的产生和发展，使人们在结构损伤状态的评估中，可对无法直接用计算来表现和利用的信息，在参考专家意见和考虑维修费用、失效后果等方面因素后，使之数量化(即赋予一定的隶属度)，用模糊数学方法进行有关的推理运算，得出结构的破损状态。

本文在对已有的各种结构耐久性评估方法进行研究和分析的基础上，拟将评估等级分为5个等级，给出服从梯形或半梯形分布的隶属函数，来确定构件耐久性影响因素对各个等级的隶属度。本方法可用于多种类型的桥梁评估，具有普遍性。对既有钢筋混凝土桥梁耐久性评估大致分为实际调查、耐久性检测和进行耐久性评估3个部分。

3.1 模糊综合评估模型

本文基于层次性原则，参照现行《危险房屋鉴定标准》[3]，将桥梁结构划分成上部结构、下部结构、桥面系及附属设施3个组成部分。对桥梁耐久性评估的最低层次-构件，采用如下方法划分：

（1）上部结构：

梁：以一个孔径、一根为一构件。

板：现浇板以一个自然间面积为一构件；预制板以一块为一构件。

拱圈、架等：以一块为一构件。

支座：以一个支座为一构件。

（2）下部结构：

桥墩及基础：以单个桥墩及基础为一构件。

桥台及基础：以单个桥台及基础为一构件。

锥坡、护坡：以一自然间的一面为一构件。

调治构造物：按照危险房屋鉴定标准[3]第4.1条划分。

（3）桥面系及附属设施：

伸缩缝：以一个计算高度、一个伸缩缝为一构件。

桥头与路堤连接部：以一个连接部为一构件。

桥面铺装：以一个自然间面积为一构件。

人行道：以一个自然间面积为一构件。

栏杆、护栏：以一个自然间一轴线单面长度为一构件。

3.2 模糊综合评估步骤

影响既有钢筋混凝土桥梁结构耐久性的因素很多，因此，在对既有钢筋混凝土桥梁结构耐久性进行模糊综合评估时，采用多级模糊综合评估比较合适。本文采用三级模糊综合评估方法。

第一级评估：依据各影响因素，对桥梁结构的构件进行耐久性评估。

第二级评估：在对构件进行评估的基础上，对桥梁结构的组成部分进行耐久性评估。

第三级评估：在对组成部分进行评估的基础上，对桥梁的整体结构进行耐久性评估。

3.2.1 确定桥梁评估对象各个层次的因素集

对被评估的对象（既有桥梁结构）进行分析，将既有桥梁结构分为l个组成部分，每个组成部分分为m个构件，每个构件有n个影响因素，即：

U=[U1，U2，…，Ul]

Ul=[Ul1,Ul2…,Ulm]

Ulm=[Ulm1,Ulm2,…,Ulmn]

根据图1所示的模糊综合评估模型，建立模糊综合评估的因素集。其中调治构造物是指为引导或改变水流方向，使水流平顺地通过桥孔以减缓水流对桥位附近河床、河岸的冲刷而修建的水工构造物。如：导流堤、梨形坝、长堤、丁坝、顺坝、截水坝等。本文将其归入下部结构。

图1 模型评估综合模型

3.2.2 确定桥梁耐久性等级的评估集

V=[V1，V2，…,VJ]

无论评估层次和影响因素有多少个，其所引起的评估集只有一个集合，因此对结构、组成部分、构件以及影响因素来说，其评估集都是相同的。为了与我国现行有关规范和标准保持一致，根据桥梁的耐久性差异，可将既有桥梁的耐久性分为良好、较好、较差、差、危险5个等级，即：

V =[V1,V2,V3,V4,V5]=[良好、较好、较差、差、危险]

表1 既有钢筋混凝土桥梁结构耐久性等级的模糊划分

3.3 建立隶属函数

隶属函数是模糊集合最基本的概念，可以用隶属函数来定义模糊集合。在评估等级集V中，对任一集合VJ∈φ(u)，就确定了一个从u到uvj的一个映射：

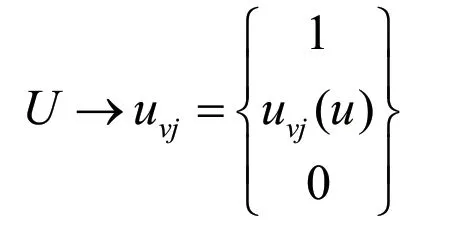
任一从u到uvj(u)的映射uvj，都惟一确定了一个子集：Vj= {u|u vj(u)=uvj}

Vj以uvj为其隶属函数，Vj的隶属函数在u处的值即为u对Vj的隶属程度。

3.4 建立因素权重集

在模糊综合评估中，因素的权重至关重要，尤其像桥梁系统耐久性，影响因素多，同层次之间、各个影响因素之间的相对重要程度，往往难以把握，即使依赖专家经验，也难以排除人为因素的影响。它反映了各个因素在综合评估中所占有的地位或所起的作用，直接影响综合评估的结果。

本文运用层次分析法确定初始权重后，提出了对第一级评估权重根据影响因素实际检测结果进行修正的更加合理确定权重的方法。对第三级评估权重，把变权原理引入到评估中，对模糊综合评估结果进行分析处理，再根据最大隶属度确定被评估对象的等级归属。对第二级的权重未加处理，采用专家给出的初始权重。

3.5 一级模糊综合评估

这是对既有桥梁结构各构件层次的模糊综合评估，也是既有桥梁结构耐久性综合评估的最基本、最重要的部分。由于对既有桥梁结构耐久性的三级模糊综合评估是按影响因素、构件、组成部分、整体结构的层次顺序由下向上逐级进行的。前一级模糊综合评估的结果是后一级综合评估的输入数据，即后一级综合评估的结果正确与否是由前一级模糊综合评估决定的，因此最底层因素的模糊综合评估是对既有桥梁耐久性模糊综合评估的基础，它的评估结果正确与否对整个既有桥梁耐久性的最终评估起着至关重要的作用。

假定论域

Ulm为欲评估的钢筋混凝土构件(如：上部主要承重构件，上部一般承重构件，桥台及基础，桥墩及基础等)的全体。在论域Ulm中随机抽取一组样本进行检测，然后依据检测结果，首先对影响其耐久性的各影响因素进行单因素评估，例如对上部主要承重构件U11进行评估，U11=[钢筋锈蚀，混凝土碳化，氯离子侵蚀，混凝土强度，混凝土裂缝，混凝土破损]，根据因素集U11中单因素的隶属函数，确定单因素U11n的评估等级的隶属度由此得出第n个因素的单因素评估集，同理依次求得各个因素的评估集，这样就得出上部主要承重构件的评判矩阵。

最后，根据获得各构件的评估矩阵和相应的权重向量，利用模糊合成运算法则，便可求出各构件耐久性的模糊综合评估结果。

对于既有钢筋混凝土桥梁结构耐久性评估，其运算式为：

式中：i—因素数，i=1,2,...,n；

j—评估等级，j=1,2,3,4,5；

ai—因素Ui的权重；

rij—因素Ui隶属于Vij等级的程度；

bj—评估结果隶属于Vj等级的程度；

这种模糊综合评估模型的特点是在决定各因素的评估对等级Vj隶属度bj时，保留了单因素评估的全部信息，对所有因素的影响均加以考虑，而不只是考虑对bj影响最大的因素，所以比较适用于既有钢筋混凝土桥梁结构耐久性评估的要求。

3.6 二级模糊综合评估

这是对组成部分层次的模糊综合评估。根据各构件的一级综合评估结果，即上部主要承重构件，上部一般承重构件，支座;桥台及基础，桥墩及基础，地基冲刷，调治构造物，桥面铺装，伸缩缝，桥头跳车，其它部件;便可得到各组成部分模糊综合评估的评估矩阵。对于上部结构而言，它的评估矩阵为;

同样，利用3.4节的权重计算方法，根据各构件对子结构的重要性失效造成损失的严重性，可求得上部结构的权重集：

进而，可求出桥梁整体结构耐久性的模糊综合评估结果

3.7 耐久性整体损伤值

由于影响结构耐久性因素的多样性、复杂性、不确定性，目前耐久性研究大多基于模糊数学等理论，所以评估的结果是一个向量而非一个点值。这就为如何由评估的结果向量确定出桥梁耐久性的整体损伤值提出了问题。也就是说，假如桥梁的整体损伤值区间为[0,1]或[0,100]，那么耐久性评估的结果是多少？目前对这一问题的研究成果还很少。

本文采用加权平均法把评估结果向量转化为确定的量值。以Bj作为权数，对各个评估等级进行加权平均，取此平均值作为评估结果，即整体损伤值。

其中：δ—耐久性整体损伤值；

bj—评估结果向量；

H相当于对综合隶属度进行综合评分，j为耐久性等级类别。根据H的计算值与哪一个等级j最接近，即可判断该桥梁结构属于（或接近）该等级。对于既有钢筋混凝土桥梁结构，在定期进行检测后，根据模糊综合评估结果和公式，即可获得既有桥梁按定期时间间隔的耐久性整体损伤值序列，然后用于本文后面提出的基于灰色动态系统理论的剩余使用寿命预测理论进行既有钢筋混凝土桥梁结构剩余使用寿命的预测。

把变权原理引入到评估中，对模糊综合评估结果进行分析处理，从而最终确定被评估对象的等级归属。变权综合原理不仅考虑了对各目标相对重要性的偏好，而且考虑了目标对均衡程度的偏好。它体现了客观事物的评估应该随着过程的具体变化而不断变化的实际。并且通过与比较成熟的贴近度法的评估结果对比，表明运用变权原理所得出的结果也是比较可信的。

4 结论

随着当前大量既有钢筋混凝土桥梁结构耐久性问题越来越突出，对耐久性评估方法的研究已引起行业内和工程界的普遍关注。本文在总结目前国内外桥梁评估研究成果的基础上，对既有钢筋混凝土桥梁结构耐久性评估和剩余使用寿命预测进行了研究，建立了基于层次分析法的三级模糊综合评估系统，该方法考虑了不同损伤程度的影响因素对评估结果的不同贡献，实现了主观（专家的知识和经验）和客观（实际检测结果）的结合，避免了单纯依靠专家的知识和经验计算权重的主观性，该方法更加合理。

既有钢筋混凝土桥梁结构的耐久性评估和剩余使用寿命预测是一个涉及知识领域十分广阔、需要不断深入研究的复杂课题。本文所提出的理论和方法，具有一定的实用意义，并且也为今后这方面进一步研究提供了参考。但由于课题的复杂性，在很多具体问题的研究方面尚需进一步的努力。

[1]金伟良，赵羽习，混凝土结构耐久性[M]，北京：科学出版社，2002，1-9.

[2]李田，刘西拉，混凝土结构的耐久性分析与设计，北京：科学出版社，1999.

[3]董传洲,混凝土桥梁耐久性模糊综合评价,[硕士学位论文],武汉：武汉理工大学,2004.