交错级数比较和比值判别法探讨

蔺梦阳

(南开大学经济学院， 天津 300071)

0 引 言

高等数学中交错级数敛散性的判别有莱布尼兹判别法，即：对交错级数

(1)

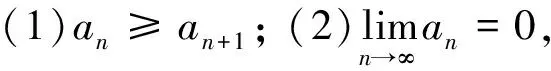
1 交错级数比较和比值判别法讨论

我们知道，正项级数有比较判别法[6]，那么，交错级数有没有和正项级数类似的比较判别法呢？下面进行一些讨论.

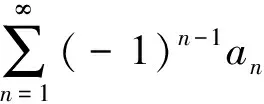
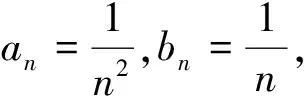
对于“问题1.1”，用正项级数的比较判别法，可以得到下面的结论：

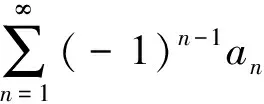
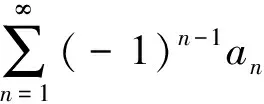
例1.3取交错级数

(2)

和

(3)

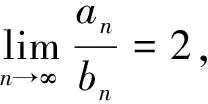
例1.4交错级数

(4)

和

(5)

从上面两个问题的讨论中可以看到，交错级数有它的特殊性，正项级数的比较判别法和比值判别法不能类比到交错级数上来.

对于交错级数(1)，如果an(an>0)本身满足某些条件，可以得到交错级数绝对收敛的一些判定结论，下面定理1.2和1.3 的证明见文献[7].

(1)当ρ<1时，交错级数(1)绝对收敛；

(2)当ρ>1或ρ=+∞时，交错级数(1)发散.

(1)当ρ<1时，交错级数(1)绝对收敛；

(2)当ρ>1或ρ=+∞时，交错级数(1)发散.

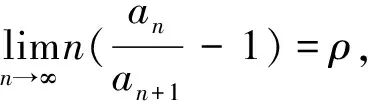
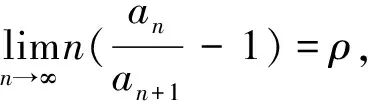
即

(6)

一方面，由于0<ε<ρ，显然有

另一方面，对(6)令n从N开始进行连乘到N+k，则有

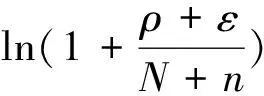
类似于定理1.4的证明，可以得到定理1.4的另外一种表示形式如下：

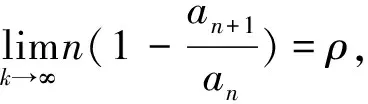
2 正项级数收敛性判别法在交错级数敛散性上的应用

对于正项级数

(7)

如果它收敛，那么交错级数(1)就绝对收敛，因此可以把关于正项级数的许多判别方法应用到交错级数绝对收敛性判别上来.上面的定理1.2和1.3就是这方面的应用，此外，还有其它更好的结论.

(1)当0<ρ<1时，交错级数(1)条件收敛，ρ>1时，交错级数(1)绝对收敛；

(2)当ρ=1时，交错级数(1)可能是条件收敛，也可能是绝对收敛；

(3)当ρ=0时，交错级数(1)可能是收敛，也可能是发散；

(4)当ρ<0时，交错级数(1)发散.

引理2.2[8]对于交错级数

(8)

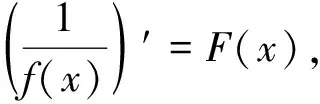
(1)当0<ρ<1时，交错级数(2.2)条件收敛，ρ>1时，交错级数(2.2)绝对收敛；

(2)当ρ=1时，交错级数(2.2)可能是条件收敛，也可能是绝对收敛；

(3)当ρ=0时，交错级数(2.2)可能是收敛，也可能是发散；

(4)当ρ<0时，交错级数(2.2)发散.

3 应用举例

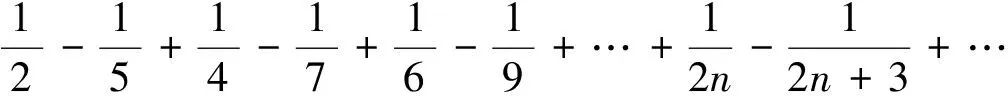
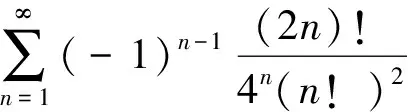
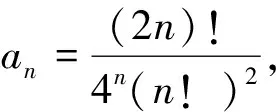
所以交错级数收敛.

参考文献

[1] 刘志高.交错级数的对数判别法[J].大学数学，2010，26(2):194-196.

[2] 钱伟懿.交错级数敛散性的一个新判别准则[J].高师理科学刊，2009，29(2):8-9.

[3] 蔡 敏，龚水法.交错级数收敛性的几个结果及其应用[J].高等数学研究,2009, 12(3):29-31.

[4] 宋文超，董国雄，龚东山.一类交错级数的敛散性判定[J].高师理科学刊，2010，30(4): 9-11.

[5] 王宣欣.交错级数敛散性的判别方法[J].山东广播电视大学学报，2010，2：66-67.

[6] 孙兰敏，张 平.双项交错级数敛散性的判定[J].衡水学院学报，2008，10(1)：5-6，19.

[7] 张效成，张 阳，徐 锬.经济类数学分析(下)[M].天津：天津大学出版社，2006.

[8] 郑玉敏，刘玉娟.交错级数敛散性的微分形式判别法[J].高等数学研究,2010,13(3): 6-7.