考虑空气阻力时大角度单摆的周期研究
肖波齐, 兰金标, 张 伟, 李秋杰
(三明学院物理与机电工程系, 福建 三明 365004)
0 引 言
单摆的周期是物理学中的一个重要问题.在大学物理的力学教学中都要研究单摆,单摆周期的求解有许多种近似方法[1-9],如余弦函数近似法、抛物线函数近似法、叠代法等[1].建立物理模型是研究和解决物理问题的关键,而单摆模型是讨论和处理有关单摆运动必不可少的要素,尤其是对于研究单摆的运动周期.由于单摆或者类单摆的运动都是在一定的环境中进行,在运动过程中或多或少会受到阻力的作用,而笔者所看到的很多有阻力的单摆的研究文献都是基于小角度情况下的,因此具有一定的局限性.在小角度下,一般在θ≤5°考虑,过于简单和理想化,而在很多情况下单摆的摆角都是大于5°.
在研究单摆问题时,大部分的学者都是运用近似方法对sinθ角度近似(角度近似也都是通过三角函数近似或者二倍角近似),最终使单摆公式简化,得到比较简单的单摆运动学方程,从而分析其周期T和一些因素(摆角、摆长、小球半径、阻尼介质等)的关系.也有的是直接分析所得到的单摆运动学方程,然后经过计算机模拟得到其运动轨迹图像,从图像中来研究单摆现象.
笔者在本文中通过对空气阻力大摆角单摆的方程进行近似,运用泰勒级数展开sinθ,用大角近似,然后运用导数微分方法计算单摆的运动学方程,通过严格的数学推导计算出周期T0,该方法避免了在解周期T时十分复杂和困难的积分运算.在空气阻力下大角度的研究对单摆周期的理论有重要的意义和科学价值,本文的研究成果对单摆的理论认识具有很好的指导作用.
1 考虑空气阻力时大角度单摆运动学方程及其解析解
与理想的单摆的模型相比,本模型考虑到空气阻力及单摆运动的角度较大(90°>θ>5°).单摆在受到阻力、驱动力下由牛顿第二定理可知运动学方程为:
(1)

公式(1)在没有驱动力的情况下可以转化为:
(2)
在大摆角情况下sinθ可按级数展开:
sinθ=θ-θ3/3!+θ5/5!-…
(3)
当θ=π/2时,θ3/3!≈0.645,θ5/5!≈0.079 5<<0.645,θ7/7!≈0.004 665<<0.079 5,θ9/9!<<0.004 665,……, 所以如果θ的取值范围在θ<π/2时,该级数是收敛的, 我们后面的讨论也是在θ<π/2的范围内进行的,这样可以省略(3)式5次方以上的项,得到:
sinθ=θ-θ3/3!
(4)
将(4)式代入(2)式中得:
(5)
已有文献得到在大角度和有阻尼时单摆的运动方程的解析解为[3]:
θ=θ0e-β tsin(ωt)
(6)
对(6)式求一阶和二阶导数:
(7)
(8)
式(8)中β>0,t>0,可知e-β t和e-3β t指数函数图像取右端的一部分,它们在[0~1]取值,故在误差范围内误差比较小,可近似得到:
e-β t≈e-3β t
(9)
分别将(6)式与(9)式代入(4)式近似得到:
(10)
又因为:
sin3(ωt)]=[3sin(ωt)-sin(3ωt)]/4
(11)
将(11)式代入(10)式进行近似得到:
(12)
然后将(7)、(8)及(12)式一起代入(2)式可得:

(13)
(13)式两边同时除以(6)式可得:
(14 )
整理(14)式可得:
(15)
又由周期T=2π/ω,可以得到在考虑空气阻力下大角度单摆的周期为:
(16)
在理想情况下单摆的周期为:
T0=2π/ω0
(17)
在考虑空气阻力下大角度单摆的周期T与在理想情况下单摆的周期T0的比值为:
(18)

2 结果分析
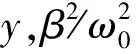

表1 x=θ0π/180与y=T0/T的关系
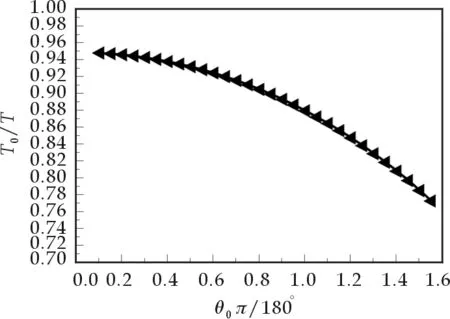
图1 y=T0/T与x=θ0π/180的关系曲线
从图1可以看出,随着弧度的增大,T0/T的值是减小的.T0/T与θ0的关系曲线呈下降趋势,这是与实际情况符合的,因为如果我们考虑空气阻力,则大角度单摆的周期T是随着角度的增大而增大的.
3 结束语
本文在考虑空气阻力情况下推导出大角度单摆的动力学方程近似解,在这里进行近似的目的是为了将大角度单摆的动力学方程用数学方法来简化,运用导数与微分的方法来计算单摆的运动学方程, 通过严格的数学推导得到其周期T,该方法避免了在解周期T时十分复杂和困难的积分运算.在空气阻力下的大角度的研究对单摆周期的理论有重要的意义和科学价值.本文的研究成果对单摆的理论认识具有很好的指导作用,有助于日常生活中一些类单摆的动力学运动问题的解决.有空气阻力大摆角单摆的运动学研究充实了对单摆的研究,而且该近似方法的运用能够使一些复杂的问题和公式得以简化. 当然本问题的近似解与精确解相比还存在一定的误差,这也是今后需要改进的,有待于我们进行进一步的研究.
参考文献
[1] 熊化高,陈 浩.有阻尼单摆的冲击波解[J].大学物理, 2007,26 (12):18-21.
[2] 陈向华,赵国忠.非线性单摆运动的数值解[J].内蒙古科技大学学报,2007,26 (1): 94-96.
[3] 刘国跃,龚劲涛,吴 英,等.单摆运动的非谐振和弱阻尼修正[J]. 绵阳师范学院学报, 2007,26(2):38-41.
[4] 谭志中. 大摆角单摆运动周期的三个公式[J]. 广西物理, 2003, 24 (3): 28-30.
[5] 叶慧群. 单摆周期近似解法综述[J]. 浙江师范大学学报(自然科学报), 2004, 27 (3): 246-250.
[6] 孙春峰. 非线性单摆的格林函数解法[J]. 大学物理,2004, 23 (1): 9-11.
[7] 谭志中. 求大摆角单摆周期近似解的“局部常化”方法[J]. 大学物理,2005,24 (12):14-17.
[8] 张风雷,鞠衍清. 另一个单摆周期近似公式[J]. 齐齐哈尔大学学报(自然科学版),2008,24(5):76-78.

