支撑向量机的若干医学应用研究

胡灵芝

(陕西中医学院基础医学院， 陕西 咸阳 712046)

0 引 言

标准的支撑向量机因具有数学形式简单、几何解释直观、全局最优、学习速度快、泛化能力优良、适合处理高维数据等特点而被成功地用于许多分类和回归的问题中.在医学上，利用模式识别技术对不同的病情症状进行正确的分类和识别时，常用的算法是支撑向量机.但在不同的研究领域，根据其样本和要求的不同，应采用不同的训练方法，现以舌色、肿瘤等几个例子说明不同领域中所用到的不同的支撑向量机训练过程.

1 算法原理

支撑向量机是基于线性可分情况下的最优超平面提出的，其基本思想概括为：首先通过非线性变换将输入空间变换到一个高维空间，然后在这个新空间中求最优线性超平面，而线性变换是通过核函数实现的.

线性支撑向量机的算法如下：

(1)用H=D[A-e]定义矩阵H；

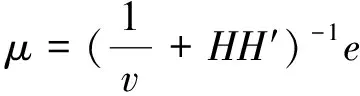
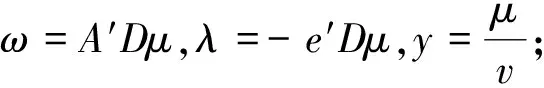
非线性支撑向量机的算法如下：

(1)选择一个核函数K(A,A′)；

(2)用算式定义G=D[K-e]；

(3)计算拉格朗日乘子v；

(4)用K(x′,A′)Dμ-γ=K(x′,A′)DDK(A,A′)′Dv+e′Dv=(K(x′,A′)K(A,A′)′+e′)Dv=0得到非线性SVM分类超平面；

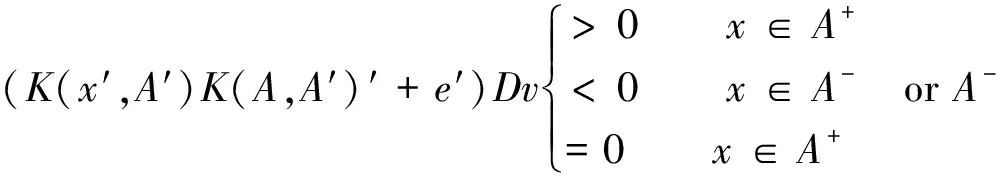
构造支撑向量机分类器首先要确定核函数的类型，采用不同的核函数将导致不同的支撑向量算法，目前得到的核函数形式主要有： 线性核函数：K(x,y)=(x·y)、 多项式核函数：k(x,y)=(x·y+1)p、 高斯核函数：k(x,y)=exp(-γ|x-y|2)、S型核函数：k(x,y)=tan(kx·y-δ).

2 支撑向量机在医学领域的应用研究

2.1 中医舌色苔色识别

舌诊是中医四诊中望诊的重要内容，是中医临床诊断的主要依据之一.传统的舌诊是根据中医医生观察来诊断病情的，诊断结果和医生的知识水平、诊断经验密切相关.为了有一个确切的诊断依据，必须将舌诊客观化，即解决舌诊的模糊性和不确定问题.计算机数字图像处理技术在这一方面具有独特的优势.

针对舌色、苔色分类与识别不仅要求具有较高的识别率，而且要求经过的分类器个数尽可能少的特点，在训练分类器的过程中，根据部分类别之间的线性可分，另一部分类别线性不可分的特点，采用不同的核函数.对于线性可分的两类问题如果采用非线性核函数，不仅计算量大，而且获得的支撑向量比较多，从而会影响识别速度和正确识别率，为此可优先采用线性核函数，在两类问题线性不可分的情况下，采用非线性核函数.如何判断两类问题是否线性可分可归结为求解如下问题：

其中α为拉格朗日系数矢量，αi为各个样本所对应的拉格朗日系数，C为惩罚项，yi为样本对应的类别标号(1或-1)，Q为核函数矩阵，N为样本总数.所得两类分类器为：

当αi=C,f(x)<0的样本，称为错分样本.采用线性核函数对样本训练完毕后，判断其是否存在错分样本，存在即线性可分，否则线性不可分.

核函数的参数选取采用交叉验证法.如样本量为750，则属于15类，每两类组合为100个样本，把这100个样本分为5组，每次取出一组作为测试数据，其他4组作为训练数据，以此类推，可得核函数参数p1=10，惩罚因子C=100，平均正确识别率为93.87%.

2.2 肿瘤形状特征分类

通常临床根据肿瘤的形态、内部回声分布等超声图像的特征对肿瘤进行良恶性的识别.利用超声图像的特征进行肿瘤良恶性的识别可采用支撑向量机.利用支撑向量机解决此类问题采用的是非线性算法，先求得其标准线性SVM如下：

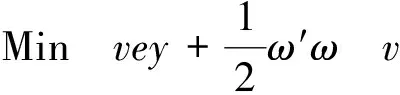
s.t.D(Aω-eγ)+y≥e，y≥0

相应的线性分类器为：

通过优化分类面的方向和位置来确定最优分类面，得到新的支撑向量机如下：

s.t.D(Aω-eγ)+y=e

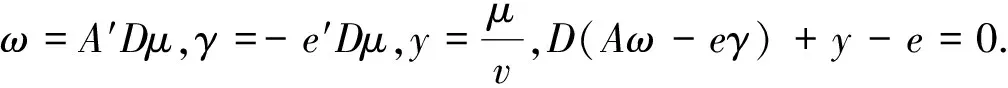
为了得到非线性分类器，将ω=A′Dμ代入上面限制条件中，并用非线性核函数K(A,A′)代替AA′，得到下式：

s.t.D(K(AA′)Dμ-eγ)+y=e

以下用K代替K(A,A′)，得到如下的拉格朗日函数(v为拉格朗日乘子)：

从KKT条件得出γ,μ,y及拉格朗日乘子v,即

(1)

非线性SVM分类面可以从线性分类面的公式中推导出来，即x′A′Dμ-γ=0. 用K(x′,A′)代替式中的内积x′A′，并将式(1)中的μ和γ代入，得到如下非线性SVM分类超平面，即

K(x′,A′)Dμ-γ=K(x′,A′)DDK(A,A′)′Dv+e′Dv=(K(x′,A′)K(A,A′)′+e′)Dv=0

相应的非线性SVMS分类器为：

可以使用上式对肿瘤样本进行分类，当良性肿瘤样本超过恶性肿瘤样本时，此算法的分类精度明显下降，反过来亦如此.

此处的核函数可选择高斯核函数，以达到较好的泛化能力和较少的参数调整.

2.3 肾结石分类

肾结石病发病率近年来呈上升趋势，同时由于该病的复发率比较高，因此探讨肾结石病的形成原因对治疗和预防具有重要的意义.SVM作为一种新型的机器学习工具被用于进行肾结石的分类.

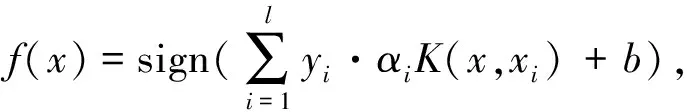
在实际训练过程中，如采用2 501个样本，可随机分成两类：用于调整模型参数的2 000个样本的训练集和用于评估预测能力的501个样本的测试集.实现SVM的计算程序可写入R文件中，用专用编译器编译，并在微机上运行.当参数C=1 000，核函数变量为1，支撑向量的数目为17时，SVM的分类准确度达到了99.95%，可见SVM对分类问题有很好的适应性.

3 结束语

线性分类器是基于数据输入空间实现分类，而非线性分类器则是基于高维特征空间用核函数代替非线性映射来实现分类，为非线性预测提供了可能.在处理不同类型的数据时，应先分析数据的空间特征，判定是否线性可分，进而采用恰当的算法，选择不同的核函数，以减少病情症状分类和识别的计算量，提高速度.支撑向量机在医学上除了上述几个应用领域之外，还可用于药物设计、蛋白质结构预测、基因识别、血细胞的分类、定量构效关系数据分析等等.

参考文献

[1] 张新峰.多类支撑向量机在中医舌质、舌苔分类和识别的应用研究[J].电路与系统学报，2004，9(5)：110-113.

[2] 王 冰.基于线性判别式和支撑向量机的肾结石分类方法[J].兰州大学学报，2006，42(2):77-80.

[3] Burbidge R,Totter M,Buxton B,etal.Drugdesign by machine learning:support vector machines for pharmaceutical data analysis[J].Computer Chem.,2001,(26):5-14.

[4] 边肇祺，张学工.模式识别[M].北京：清华大学出版社，2000.

[5] 卫保国，王爱民.一种新的多类模式识别支撑矢量机[J].模式识别与人工智能，2002，15(2)：178-181.