计算机网络病毒传播的动力学性态分析

秦 鹏， 李 红

(1.中北大学信息与通讯工程学院， 山西 太原 030051;2.太原市杏花岭区第二中学， 山西 太原 030003)

0 引 言

计算机病毒不但本身具有破坏性, 更有害的是具有传染性, 一旦病毒被复制或产生变种, 其传染速度之快令人难以预防. 传染性是病毒的基本特征. 计算机病毒会通过各种渠道从已被感染的计算机扩散到未被感染的计算机, 在某些情况下造成被感染的计算机工作失常甚至瘫痪. 与生物病毒不同的是, 计算机病毒是一段人为编制的计算机程序代码, 这段程序代码一旦进入计算机并得以执行, 它就会搜寻其他符合其传染条件的程序或存储介质, 确定目标后再将自身代码插入其中, 达到自我繁殖的目的. 只要一台计算机染毒, 如不及时处理, 那么病毒会在这台机子上迅速扩散, 其中的大量文件(一般是可执行文件)会被感染,而被感染的文件又成了新的传染源, 在与其他机器进行数据交换或通过网络接触时病毒会继续进行传染.正常的计算机程序一般是不会将自身的代码强行连接到其他程序之上的，而病毒却能使自身的代码强行传染到一切符合其传染条件的未受到传染的程序之上[1-3]. 计算机病毒可通过各种可能的渠道, 如移动硬盘、计算机网络传染给其他的计算机[4].

本文研究了新入网的计算机、从网络中被淘汰的计算机以及装有反病毒软件的计算机等因素对网络病毒的影响, 定性研究了计算机病毒在互联网中的传播规律, 为控制计算机病毒的流行提供了理论依据.

1 模型

设S(t),I(t),R(t),A(t)分别表示t时刻的易感节点(没有装反病毒软件或系统存在漏洞, 容易被感染的节点)、感染节点(已经被感染并且有感染其他节点能力的节点)、暂时免疫节点(不具有感染能力且暂时也不会被感染的节点)和装有反病毒软件的节点(装有反病毒软件且不会被感染的节点)的数量, 在单位时间里, 有C个新节点加入, 它们指新连接入网的主机;β1表示病毒对易感者节点的感染率;μ表示节点的自然死亡率;δ表示感染节点的恢复率;σ表示节点的免疫失去率;α表示易感节点受装有反病毒软件节点的影响转变成装有反病毒节点的比率;β2表示病毒受装有反病毒软件节点的感染率.

(1)

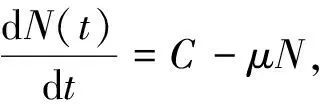
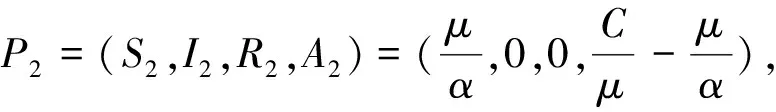
2 平衡点的稳定性分析

系统(1)在无病平衡点P1处的雅克比矩阵为:

系统(1)在无病平衡点P2处的雅克比矩阵为:

对应的特征方程为:[λ+(σ+μ)][λ-(β1S2+β2A2-(δ+μ))][λ2+(μ+αA2)λ+μαA2]=0,特征根为:-(σ+μ),β1S2+β2A2-(δ+μ),-μ,-αA2,当R01>1时,-αA2<0, 所以要想使得矩阵的特征根都具有负实部，只要使得:β1S2+β2A2-(δ+μ)<0成立, 即

因此, 当R01>1,R03<1时, 无病平衡点P2渐近稳定, 当R03>1时, 无病平衡点P2不稳定.

系统(1)在地方病平衡点P3处的雅克比矩阵为:

矩阵有一个特征根为:αS3-β2I3-μ, 其余特征根满足:

即F(λ)=λ3+a1λ2+a2λ+a3=0,其中a1=β1I3+2μ+σ>0,a2=(β1I3+μ)(μ+σ)+β12S3I3>0,a3=β12S3I3(μ+σ)-β1σδI3=β1I3(δμ+σμ+μ2)>0, 因此, 要想使得F(λ)=0的所有特征根都具有负实部, 只要a1a2-a3>0成立. 因为a1a2-a3>0恒成立, 所以F(λ)=0的3个特征根都具有负实部.

因此, 系统(1)在地方病平衡点P3处对应的特征根都具有负实部, 需要满足:αS3-β2I3-μ<0 , 即

所以, 当R02>max{1,R04}时, 地方病平衡点P3渐近稳定. 否则, 地方病平衡点P3不稳定.

综上所述:

(Ⅰ)当R01<1,R02<1时, 无病平衡点P1渐近稳定；

(Ⅱ)当R01>1时, 无病平衡点P1不稳定, 存在无病平衡点P2；

(Ⅲ)当R02>1时, 无病平衡点P1不稳定, 存在地方病平衡点P3；

(Ⅳ)当R01>1,R03<1时,无病平衡点P2渐近稳定, 当R01>1时, 无病平衡点P2不稳定；

(Ⅴ)当R02>max{1,R04}时, 地方病平衡点P3渐近稳定. 否则, 地方病平衡点P3不稳定.

3 结 论

本文中我们分析了计算机病毒的动力学行为, 通过对计算机病毒传播模型的定性分析可知, 普及提高广大用户的安全防范意识、掌握病毒防治技术是十分必要的. 例如可以通过加强计算机病毒的知识普及, 增强用户的信息安全意识, 通过及时安装反病毒软件或修补漏洞, 使计算机病毒对网络的影响降到最低.

参考文献

[1] Kephart J., White S. Directed-graph epidemiological models of computer viruses[R]. 1991 IEEE Sym-posium on Security and Privacy, 1991：343-359.

[2] Wang F.W., Zhang Y.K., Wang C.G.,etal. Stability analysis of a SEIQV epidemic model for rapid spreading worms[J]. Computers Security, 2010,29:410-418.

[3] Jose R.C. Piqueira, Vanessa O. Araujo. A modified epidemiological model for computerviruses[J]. Applied Mathematics and Computation, 2009,(213):355-360.

[4] 邓清华.计算机病毒传播模型及防御策略研究[D].武汉：华中师范大学硕士学位论文, 2009.