具有非线性传染率的病毒动力学模型的稳定性分析

王佳颖， 窦霁虹， 童姗姗

(西北大学数学系， 陕西 西安 710127)

0 引 言

随着社会的进步，病毒、传染病等字眼成为人们越来越关注的话题.所以，研究传染病模型、讨论感染是否消失以及病毒和免疫是否继续在当今社会中显得尤为重要.1997年Bonhoeffer等[1]以及2000年Nowak和May[2]建立并研究了基本的病毒动力学模型：

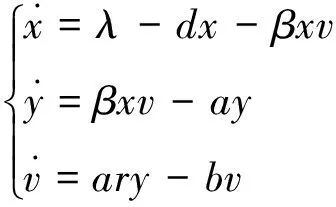
(1)

(2)

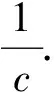
(3)

1 平衡点的分析

它表示有病毒的存在但是无免疫.

表示病毒和免疫共存.

2 平衡点的稳定性分析

证明构造Lyapunov函数：

沿系统(3)对F1(x,y,v,z)关于t求全导数可得：

(4)

定理2如果R0>1且R1≤1时，则无免疫平衡点E1是全局渐近稳定的.

证明构造Lyapunov函数

沿系统(3)，对F2(x,y,v,z)关于t求全导数，得：

由于

且当R1≤1时有

定理3如果R0>1且R1>1，正平衡点E2存在且是全局渐近稳定的.

证明构造Lyapunov函数

沿系统(3)，对F3(x,y,v,z)关于t求全导数，得：

(6)

由于

3 结束语

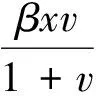
当R≤1时，即一个病人在平均染病期内能传染的最大人数不大于1时，模型仅存在无病平衡点，它是全局渐近稳定的,这时疾病就会自然逐步消亡；当R0>1且R1≤1时，模型存在全局渐近稳定的无免疫平衡点，所以此时机体已感染病毒但还未建立机体免疫反应.此时如果不采取任何措施，染病者将逐步趋于死亡；当R0>1且R1>1，宿主体内病毒和抗体共存，此时正平衡点存在且全局渐近稳定即疾病将始终存在，并进而形成地方病.

参考文献

[1] Bonhoeffer S, May R M, Shaw G Metal.. Virus dynamics and drug therapy[J].Proc Natl Acad SciUSA,1997,(94):6 971-6 976.

[2] Nowak M A, May R M. Virus Dynamics: Mathematical Principles of Immunology and Virology[M]. New York: Oxford University Press, 2000.

[3] Andrei Korobeinikov. Global properties of basic virus dynamics models[J].Bulletin of Mathematical Biology, 2004,(66):879-883.

[4] Haiyan Pang, Wendi Wang, Kaifa Wang. Global properties of virus dynamics with CTL immune response[J]. 西南师范大学学报(自然科学版), 2005,30: 796-799.

[5] Xiangyun Shi, Xueyong Zhou, Xinyu Song. Dynamical behavior of a delay virus dynamics model with CTL immune response[J].Nonlinear Analysis: Real World Applications,2010,(11):1 795-1 809.

[6] 宋 强,王 霞,吴怡静.一类带有非线性传染率的病毒动力学模型的全局稳定性[J].鞍山师范学院学报,2008,10(2): 1-3.

[7] Tsuyoshi K, Toru S. A note on the stability analysis of patheogen-immune interaction dynamics[J]. Discrete and Continuous Dynamical System Series B4, 2004 (B4): 615-622.

[8] Martin A Nowak, Charles R M Bangham. Population dynamics of immune responses to persistent viruses[J]. Science, 1996, 272:74-79.

[9] Gang Huang, Wanbiao Ma, Yasuhiro Takeuchi. Global properties for virus dynamics model with Beddington-DeAngelis functional response[J]. Applied Mathematics Letters，2009,(22):1 690-1 693.