平面曲线轮廓度误差的高斯-牛顿法评定
李 蔚, 王林艳
(西安工业大学机电工程学院, 陕西 西安 710032)
0 前 言
线轮廓度是对曲线形状的要求,是限制实际曲线对理想曲线变动量的一项指标,是零件形位公差国家标准和国际标准中应用广泛而又难以测量和评定的项目[1,2].线轮廓度误差指实际轮廓线偏离理想轮廓线的程度,用距离最小的两条与理论轮廓线处处等距的曲线包容实际轮廓线,两条等距曲线的距离即是该轮廓线的轮廓度误差.在工程领域中,对于精密传动零件的复杂曲面可以通过控制其一系列截面形状即用一系列平面曲线来表征,因而线轮廓度的评定有重要的理论意义和实用价值.由于在进行线轮廓度的精密测量时必然存在一定的安装误差,即被测轮廓的测量基准与设计基准之间存在位姿误差,会对评定结果产生影响,从而降低评定精度,因而在进行精密测量时必须进行误差分离,分离出位姿误差和轮廓度误差.线轮廓度的评定方法主要有最小二乘法、最小区域法.最小区域法建立评定的数学模型比较困难,当测量点密集时,利用最小二乘法所求解的误差曲线与实际的误差曲线非常接近,因而是最小区域法的最佳逼近,为此工程上通常采用最小二乘法进行线轮廓度误差评定.本文利用高斯-牛顿法进行了线轮廓度的误差分离,从而实现了位姿误差和线轮廓度误差的最小二乘法求解.

图1 测头半径补偿
1 测量数据的预处理
如图1所示,在用坐标法进行轮廓度测量中常采用球形测头,因此测量数据反映的是测头球心轨迹的节点坐标值,而不是被测轮廓节点坐标值.图1中,τ和n为点Pi处的切矢与法矢.在进行精密测量时,即使测头半径很小,其对评定的影响也不能忽略,因此在进行轮廓度误差评定以前需对测量数据进行预处理,即需要通过测头半径补偿将轮廓度的测量数据变换为评定数据,进行各触点法线方向的测头半径补偿[3-5].测头中心轨迹与被测轮廓互为等距曲线,将此曲线沿各测头中心点法向向轮廓表面等距平移测头半径值,实现法线方向的测头半径精确补偿.假设轮廓曲线方程为f(x,y)=0,则测头半径的补偿公式如下:
(1)
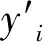
2 平面曲线轮廓度误差的评定
2.1 误差分离数学模型的建立
由于线轮廓度误差符合“小误差假设”,即被测线轮廓度误差与相应的被测曲线名义尺寸相比是微量,故可以推导出评定点Pi(xi,yi)至理论曲线的距离为di:
(2)
式中,fix和fiy分别是f(x,y)在实测点Pi(xi,yi)处对x和y的一阶偏导.
建立曲线轮廓度误差最小二乘法评定模型:
(3)
式中,n为实测曲线上的测点数目.
由于实测曲线与理论曲线之间存在着位姿误差u=[dx,dy,θ]T,因此要进行坐标变换.线轮廓度误差测量符合“小偏差假设”[6,7],即正确建立工件坐标系和进行装夹定位后,测量基准与理想基准之间的偏差和相应的曲线名义尺寸相比是微量,因而推导出坐标变换公式为:
(4)
则曲线轮廓度误差评定模型优化目标函数为:
(5)
优化问题即求向量u=[dx,dy,θ]T,使F′为最小.
2.2 位姿误差的求解
优化问题的目标函数f(x)为若干非线性函数平方和的形式,即非线性最小二乘问题,其形式可表示为
(6)
其中r(x)=(r1(x),…,rm(x))T称为在点x处的残向量[8].
结合小误差和小偏差两点假设及线轮廓度误差的定义,可以得出ri(x),i=1,2,…,m,在最优解u*处值为零或取较小值,属零残量或小残量问题,故该优化问题的求解可采用高斯-牛顿法.
函数ri(x),i=1,2,…,m,二次连续可微,则高斯-牛顿法的一阶与二阶导数分别为
g(x)=f(x)=A(x)r(x)
(7)

(8)
其中A(x)=[ri(x),…,rm(x)].
对一般无约束优化问题的牛顿类算法,在迭代点x(k)取目标函数f(x)的下列形式的二次近似:
(9)
此方程的最优解作为搜索方向或修正向量.由于ri(x),i=1,2,…,m,在最优解u*处属零残量或小残量问题,G(x)中的非线性项S(x)或为0,或同M(x)相比相对较小,故二次模型 (9) 中的矩阵Bk为f(x)在点x(k)处海森矩阵的一个近似,可取为Mk=M(x(k)),而最优解δ(k)可由方程组
(10)
确定.δ(k)为f(x)在点x(k)处的一个下降方向,在该搜索方向进行线性搜索,取
x(k+1)=x(k)+αkδ(k)
(11)
其中αk为线性搜索步长.
只进行一次优化计算,一般无法取得最优解,应采用循环迭代的方法多次进行坐标平移及转换,调整测量基准逐步逼近设计基准,直至找到最优解.
2.3 线轮廓度误差的评定
线轮廓度误差评定的求解过程如下:
(1)将实测点集根据公式(1)进行测头半径补偿,做等距曲线平移,求得评定点集.
(2)由公式(2)求解评定点集至理论轮廓曲线的距离,建立曲线轮廓度误差最小二乘法评定模型.
(3)由公式(4)建立误差优化模型.
(4)初始化,置初值向量u(0)、α(0)、允许误差e.
(5)计算f(u(k)).
(6)计算线性搜索向量δ(k).
(7)计算u(k+1),u(k+1)=u(k)+αkδ(k).
(8)计算f(u(k+1)).
(9)比较f(u(k+1))与f(u(k)),当|f(u(k+1))-f(u(k))|>e,转步(6),进入循环.|f(u(k+1))-f(u(k))| (10)将评定点集利用坐标变换转换为理想计算点集,此时所变换的点集即为消除位姿误差后与理论曲线最为匹配的点集. (11)计算点集中每一点至理想曲线的距离,正负向距离的绝对值之和最大值即为线轮廓度误差. 以测量理论曲线八分之三圆弧为例进行验证.圆弧的理论曲线方程为:x2+y2-302=0.首先从该圆上等角度每隔一度采一个点共采135个点;其次在135个点的法向上利用随机函数加上介于-10至+10 μm之间的随机误差,随机函数值的大小仿真实际曲线与理论曲线的小误差;在此基础上预加位姿误差[1,1,3]T,该向量仿真设计基准与测量基准之间的小偏差为dx、dy和θ;最后在曲线法向上等距外移0.5 mm,仿真用直径为1 mm的测头测量. (1)采用公式(1)实现曲线的等距内移,消除测头半径对测量结果的影响,结果如图2所示. (2)建立误差分离数学模型: r为圆弧半径30,n为测量点数135. (3)位姿误差求解. 根据高斯-牛顿法推导出误差分离数学模型的线性搜索方向: 令:s1=-xisinθ-yicosθ,s2=xicosθ-yisinθ,s3=xicosθ-yisinθ+dx,s4=xisinθ+yicosθ+dy. 沿下降搜索方向经多次迭代可求出最佳调整位置向量u*=[dx,dy,θ]T,即位姿误差,使得测量基准与设计基准趋于一致. 图2 测头半径补偿实例 图3 误差曲线图 实例仿真在VC++ 6.0平台上运行.第一次计算时不考虑安装误差,直接计算测量点到理论曲线的距离, 正负向距离绝对值之和的最大值为1 897 μm.第二次计算采用高斯-牛顿法进行误差分离,求得位姿误差u*=[dx,dy,θ]T=[0.995 68,1.003 45,2.998 76]T,将测量误差曲线进行坐标变换消除位姿误差对其的影响,从而计算得到正负向距离绝对值之和的最大值为20.14 μm.通过两次计算对比可以看出,第一种方法由于未考虑测量基准与设计基准不一致,测量结果偏离设定值很大,第二种方法进行了误差分离,计算结果非常逼近预先设置值(f=20 μm,u*=[1,1,3]T),是一种评定线轮廓度误差的可行方法. 仿真程序还绘制出几种误差曲线综合比较图如图3所示,图中外侧较深的细实线为测量误差曲线,内侧两条曲线中深颜色较粗的实线为消除位姿误差后的误差曲线,浅色较细的实线为被测实际误差曲线.为清楚观察误差大小,图中误差单独放大200倍.测量误差曲线包含有位姿误差,明显偏离被测实际误差曲线.消除位姿误差后的误差曲线是将测量误差曲线按计算得出的位姿误差经过坐标平移和旋转得到,与被测实际曲线趋于一致,在此情况下再进行误差评定其结果必然会趋近真实值. 本文在线轮廓度误差评定中通过测头半径补偿消除测头对测量结果的影响,建立了误差分离数学模型,根据模型特点采用高斯-牛顿法求解出位姿误差和线轮廓度误差,通过计算机仿真中误差曲线图和计算结果的双重对比得出在小误差和小偏差假设前提下,采用高斯-牛顿法进行线轮廓度误差分离简单可行.但对于采用较低精度设备所得的测量结果,不满足小误差和小偏差条件,采用何种方法进行误差分离需进一步探讨. 参考文献 [1] 刘文文,聂恒敬.一种自适应的平面线轮廓度误差评定方法[J].计量学报,1999,20(1):27. [2] 廖念钊,古莹菴,莫雨松.互换性与技术测量[M].北京:中国计量出版社,2007. [3] 侯 宇,张 竞,崔晨阳.复杂线轮廓度误差评定方法[J].仪器仪表学报,2001,22(1):104. [4] 侯 宇,张 竞,崔晨阳.复杂线轮廓度误差坐标测量的数据处理方法[J].计量学报,2002,23(1):13. [5] 苏步青,华宣积.实用微分几何引论[M].北京:科学出版社,1986. [6] 熊有伦.精密测量的数学方法[M].北京:中国计量出版社,1987. [7] 陈朝光,唐余勇,吴鸿业.微分几何及其在机械工程中的应用[M].哈尔滨:哈尔滨工业大学出版社,1998. [8] 徐成贤,陈志平,李乃成.近代优化方法[M].北京:科学出版社,2002.3 实验仿真
3.1 仿真数据
3.2 仿真过程

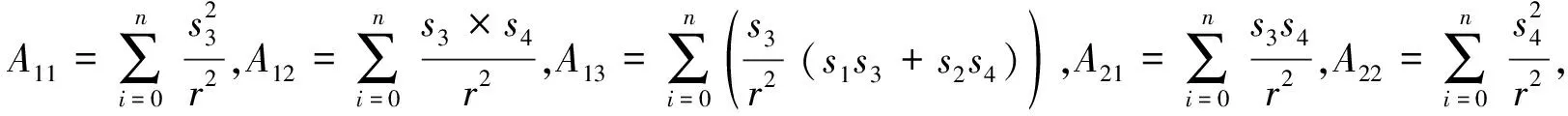
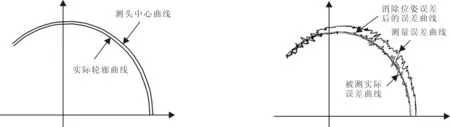
3.3 仿真结果
4 结束语

