大功率400Hz 逆变电源数字控制设计
刘春喜 马伟明 孙 驰 胡文华
(1.浙江大学电气工程学院 杭州 310027 2.海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033 3.华中科技大学电气工程学院 武汉 430074 4.辽宁工程技术大学电气与控制学院 葫芦岛 125105)
1 引言
大功率中频400Hz/115V 逆变器基波频率高,输出电流大,为保证逆变器的可靠性和工作效率,开关频率不宜过高,导致逆变桥输出的谐波含量较大[1]。为了滤除这些谐波,要求滤波器截止频率必须较低,这又会限制控制带宽的扩展,给波形质量控制带来困难。采用传统的PI 或PID 控制器,低频时控制器的增益有限,稳态误差较大[2-3]。而且,数字控制执行时由采样、计算及数字PWM 等过程产生的延时对系统的动态和稳态特性会产生较大影 响[4-5]。文献[6-7]中介绍的基于两级H 桥结构的逆变器可以得到较高的等效开关频率,降低输出电压谐波,但是并没有对数字控制引入的延时进行详细分析。近来众多文献介绍的P+谐振控制[8-11],可以消除稳态误差,且实现方便,但多用于工频或中小功率场合,在中频大功率场合的应用还很少。本文把两级H 桥结构和P+谐振控制用于400Hz/115V逆变器,对数字控制时的采样、计算和PWM 延时进行了分析,通过在连续域设计中引入等效延时环节的方法对数字控制参数进行近似设计。
2 两级H 桥逆变器结构分析
两级H 桥逆变器结构如图1a 所示,Ed为直流侧电压,nT为变压器一次和二次的匝比,L、C 分别为逆变器输出滤波电感和电容,r 表示滤波电感等效串联电阻、死区效应等各种阻尼因素的综合等效电阻。反馈变量v 被检测后,经采样、A/D 转换,变成数字量输入至处理器中,按照所设计的控制规律,求得控制量的调制信号 m(t),存储并输出到DPWM 模块,与载波进行比较,得到控制脉冲信号,这些信号经驱动电路放大后去控制开关管。
单个H 桥采用单极性控制,两个H 桥的输出经变压器二次侧串联在一起,它们之间采用交错控制技术。自然采样PWM 波形时序如图1b 所示。调制波为us,载波c(t)由四个三角波uc1、uc2、uc3、uc4组成,周期都为T,幅值为cpk,uc1、uc3、uc2、uc4相位依次相差π/2。us与uc1、uc2、uc3、uc4相比较分别产生四对互补的开关信号ug1和ug2、ug3和ug4、ug5和ug6、ug7和ug8,分别去控制八个开关管的导通与关断。当us>uc1时,ug1为高电平1;当us<uc1时,ug1为低电平0,其他比较类似。若变压器为理想变压器,且匝比为1,则变压器二次电压uT为


图1 两级H 桥逆变电路及其自然采样PWM 波形 Fig.1 The topology of single phase inverter and waveforms
在后文分析中,认为调制周期Tm为三角波周期T 的1/4,两级H 桥的等效开关频率fm为实际开关频率f 的4 倍。
3 采样、控制计算和DPWM 延时分析
3.1 采样、控制计算延时
数字执行过程中,采样、控制计算需要一定的时间才能完成。如果在一个调制周期内完成占空比的计算和输出,计算延时会使得当前周期计算出的占空比有效范围变低[12]。为使DPWM 控制正确实现,一般采用滞后一拍控制,用当前周期计算的控制量推迟一个周期去改变下一周期的占空比。为实现方便,DPWM 逆变电源一般取采样频率 fs=fm(单更新采样模式)或fs=2fm(双更新采样模式),如图2 所示。
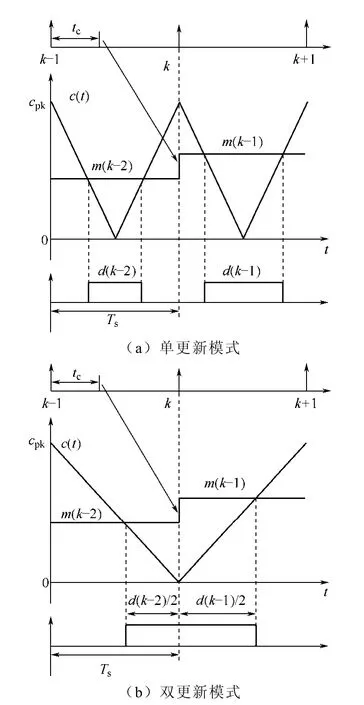
图2 滞后一拍控制时序图 Fig.2 The control sequence with one sampling period delay
图2 中只画出了载波c(t)的正半波部分,Ts为采样周期,tc为实际的采样、计算时间,m(k)为第k个采样周期得到的占空比数据,d(k)为m(k)决定的脉冲宽度与采样周期的比值。单更新采样在一个调制周期内对变量采样一次,采样点在调制周期的起始时刻(或中点时刻),采样、计算延时为一个调制周期 Tm;双更新采样在一个调制周期内采样两次,采样点在调制周期的起始和中点时刻,采样、计算延时为Tm/2。
3.2 两级H 桥DPWM 延时
用数字方法实现PWM 时,由于调制信号和载波信号都是数字信号,所以从DPWM 输入变化到占空比发生相应变化之间也有一定时间延时。
在工程中常常采用状态空间平均法将逆变系统等效为线性系统。DPWM 部分的输入为控制器输出的调节信号 m(t),输出为八个数字脉冲信号um,它们经过驱动电路后变为模拟信号去控制功率开关管的导通和关断,在变压器二次侧得到方波电压uT(t)。
由图1b 可知,在正半周,当m(t)<cpk/2 时,uT(t)包含0 和Ed两种幅值的电平信号;当m(t)>cpk/2时,uT(t)则包含Ed和2Ed两种幅值的电平信号;为了便于分析,令幅值为Ed的电平信号在一个调制周期内持续的时间与调制周期的比为D1,幅值为2Ed的电平信号在一个调制周期内持续的时间与调制周期的比为D2。当m(t)<cpk/2 时,D2=0;当m(t)>cpk/2 时,D1=1。
单更新模式采样时,一个调制周期内对调制波采样一次,采样时刻如图3a 所示,1、2、3、4 是一个三角波周期中的四个采样点。调制信号采样后进行保持,然后与三角波比较,产生相应的PWM脉冲。由于比较点所用的占空比数据是上一个采样点的占空比数据,因此DPWM 将会引入延时。对m(t)采样保持后的信号为ms(t)。因为幅值为Ed的电 平在一个调制周期内关于中点对称。这样图中Ⅰ时刻的 ms(t)相对于 1 时刻 m(t)的延时近似为(1−D1)Tm/2,Ⅱ时刻的ms(t)相对于1 时刻m(t)的延时近似为(1+D1)Tm/2。
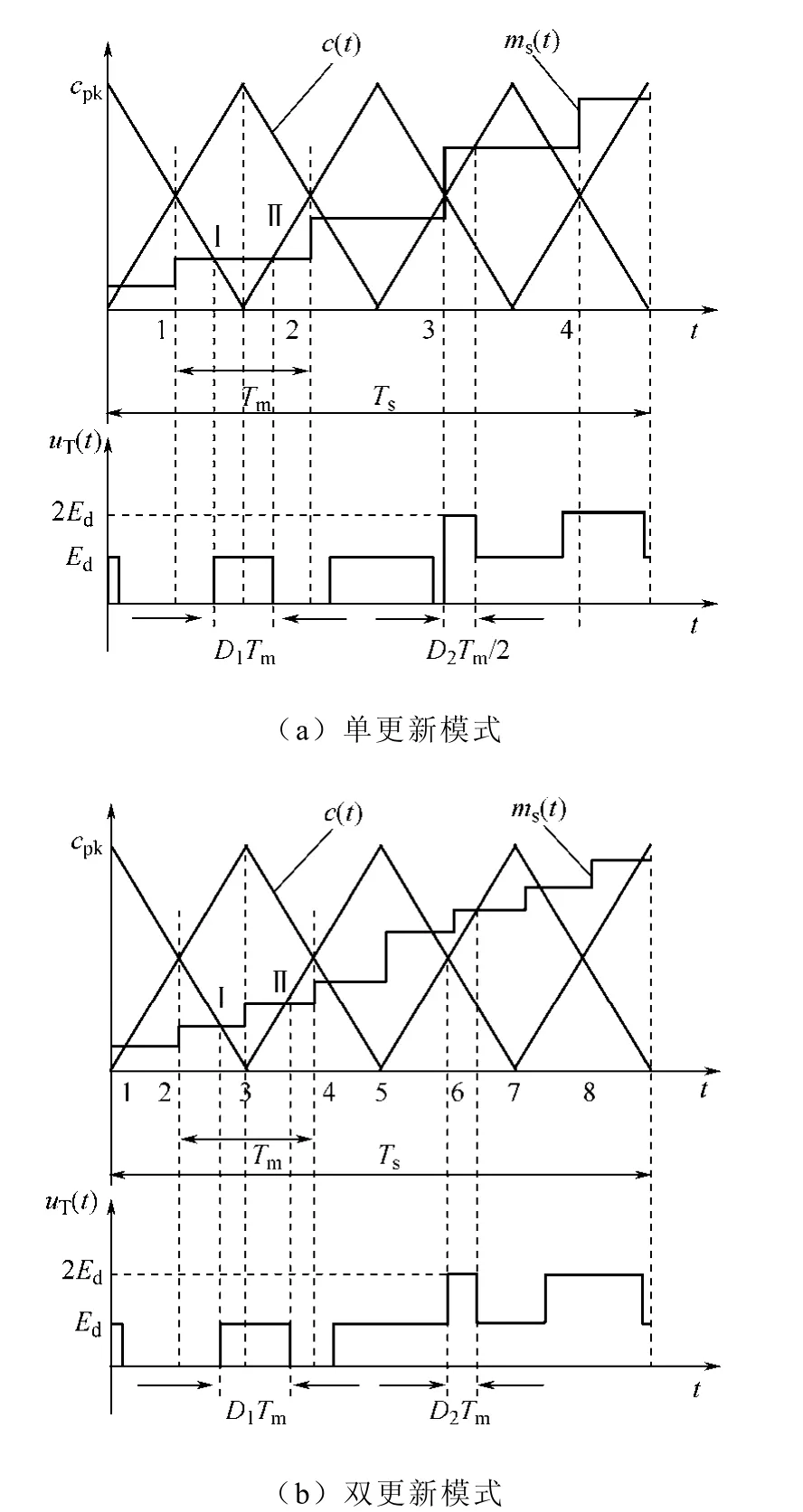
图3 DPWM 调制分析 Fig.3 DPWM modulation
当m(t)<cpk/2 时,根据平均值模型分析方法,uT(s)的基波分量uT1(s)为(本文中函数f (s)为函数f (t)的拉普拉斯变换)
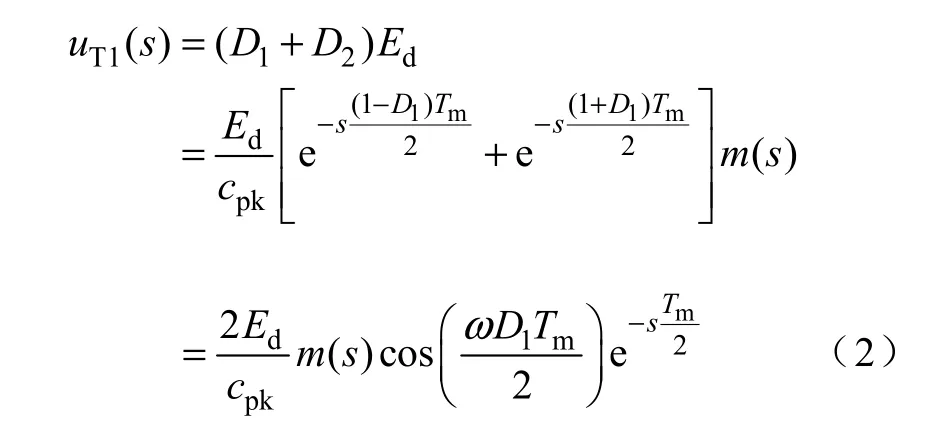
式中,s=jω。对于频率远小于调制频率的信号,ωTm≈0,上式近似为
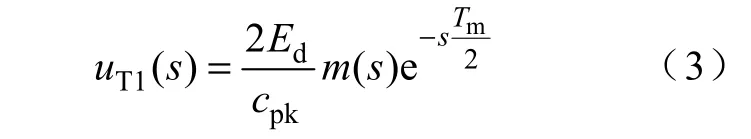
当m(t)>cpk/2 时,同理有
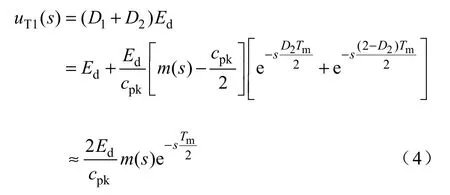
双更新模式采样时,一个调制周期内对调制波采样两次,采样时刻如图 3b 所示,1、2,…,8代表一个三角波周期中的八个采样点。因为调制频率远大于基波频率,2、3 两点间的调制波信号变化很小,可近似地认为幅值为Ed的电平在一个调制周期内关于中点对称。这样图中Ⅰ时刻的 ms(t)相对于2 时刻m(t)的延时近似为(1−D1)Tm/2,Ⅱ时刻的ms(t)相对于3 时刻m(t)的延时近似为D1Tm/2。同理,根据平均值模型分析方法,uT(t)的基波分量uT1(t)为
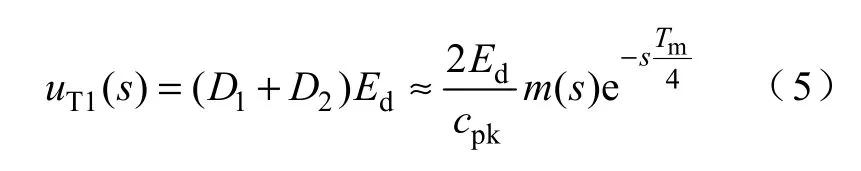
从DPWM 输入到两级H 桥输出的传递函数可表示为
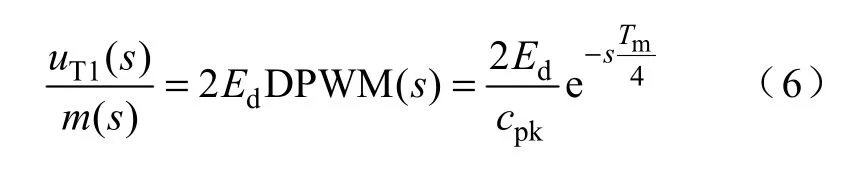
当调制波频率和LC 滤波器的截止频率相对于开关频率足够低时,两级 H 桥可看作一个增益为2Ud的比例环节,DPWM 可以等效为一个具有Ts/2延时的比例环节,比例增益为1/cpk。由于实际应用中m(t)、cpk取相同的定标,可认为cpk=1,m(t)亦为归一化调制信号,两级H 桥可等效为增益为2Ud的比例环节,DPWM 过程可近似为延时时间Ts/2 的延时环节,与零阶保持器相同。双更新采样模式的采样频率是单更新采样模式的 2 倍,因此它的DPWM 延时是单更新采样的1/2。
3.3 总的延时
一拍延时控制时,采样、计算过程会引入一个采样周期Ts的延时,DPWM 过程引入Ts/2 的延时,因此,控制器的总延时为3Ts/2。调制器和两级H桥可通过两个独立模块的串联来模拟,一个模块是静态增益,另一个是延时环节。
由于延时时间td引起的相位滞后Δθ 为

式中 fo—基波频率,取400Hz。
4 系统控制结构
图4 给出了逆变器系统的控制方框图,所有组成部分用各自的传递函数和增益表示。采用双环控制,电容电流内环和输出电压外环。对直流侧电压和输出电压进行了前馈解耦。Z(s)表示未知负载,iL、iC和io分别是流过电感、电容及负载的电流;Gi(s)、Gv(s)表示内外环控制器,内环采用比例控制器,Gi(s)=Ki;外环采用比例谐振控制,Gv(s)为[9]
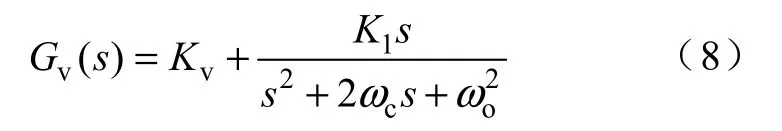
式中 Kv—外环比例系数;
K1—谐振系数;
ωc—谐振控制器低频截止角频率;
ωo—基波角频率。
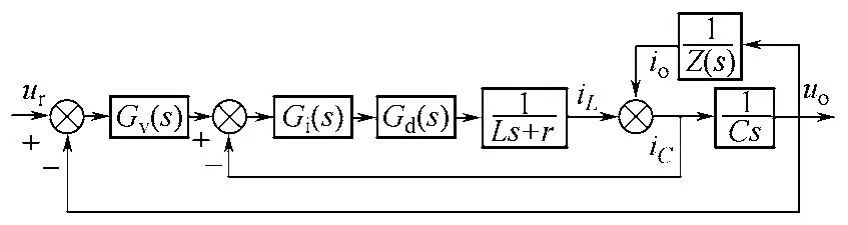
图4 系统控制方框图 Fig.4 The control block diagram of the system
Gd(s)表示数字控制器采样、计算过程引入的延时。若延时时间为3Ts/2,那么

该函数在整个复平面是解析的,没有有限的极点和零点。对所有的ω,有
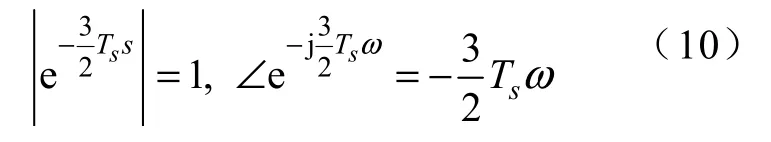
因此延时只影响系统相频特性,不影响幅频特性。延时越大,系统的相位滞后越大。为了分析方便,可用一阶pade 近似来表示延时环节。即
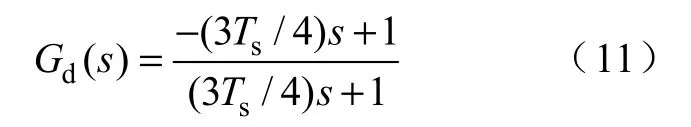
系统在空载时最不容易稳定,因此设计时必须保证系统空载运行时稳定。空载时,内环开环传递函数为
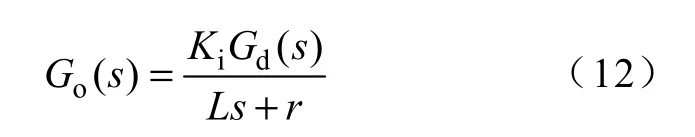
内环闭环传递函数为

外环开环传递函数为
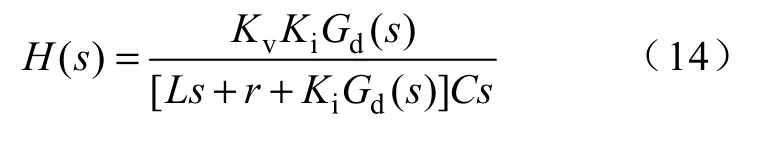
5 实例设计
单相逆变器功率容量为100kVA,输出电压为115V,逆变器各参数见表1。单更新采样模式,采样频率fs取11.2kHz;双更新采样模式,fs取22.4kHz。
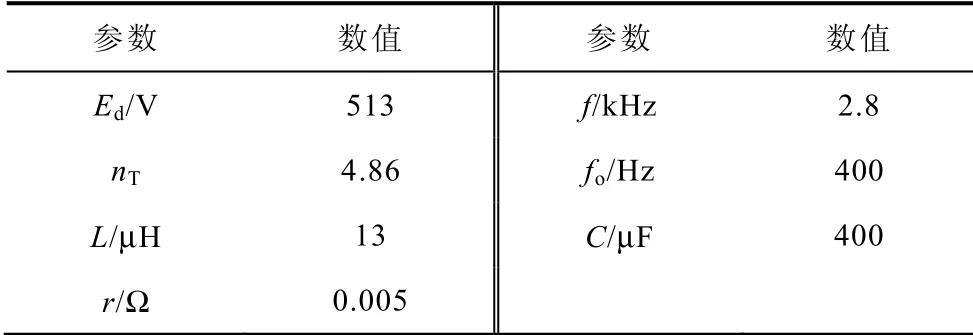
表1 仿真模型参数 Tab.1 Simulation parameters
5.1 内环设计
由式(13),根据劳斯稳定判据可得内环稳定时
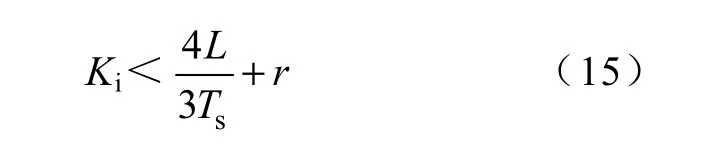
fs取11.2kHz 时,Ki<0.199;fs取22.4kHz 时,Ki<0.393。所以,Ts越小,保证内环稳定的Ki范围越大。
单更新采样模式和双更新采样模式时,分别选取Ki为0.1 和0.2。内环的幅值裕量分别为5.98dB和5.87dB,相角裕量分别为38.4°和36.9°。穿越频率分别为1.22kHz 和2.45kHz。所以单更新采样模式时的内环带宽要比双更新模式时小很多。
5.2 外环设计
与比例控制器相比,P+谐振控制器只是在谐振点对系统的频率特性有影响,在其他点影响很小。因此设计外环时,先不考虑谐振控制器,仅采用比例控制来设计,然后再设计合适的谐振系统。
根据外环开环传递函数式(14),fs取11.2kHz和22.4kHz 时,对应的Ki分别取0.1 和0.2,Kv变化时外环的根轨迹如图5 所示。由图可知,单更新采样时,Kv<2.12 时外环稳定;双更新采样时,Kv<4.07 时外环稳定。两种情况下,分别选取Kv为1.1 和2.1,对应的外环幅值裕量分别为5.7dB 和5.75dB,相角裕量分别为68.7°和69.2°。开环穿越频率分别为446Hz 和870Hz。所以单更新采样模式时的外环带宽要比双更新模式时小很多。
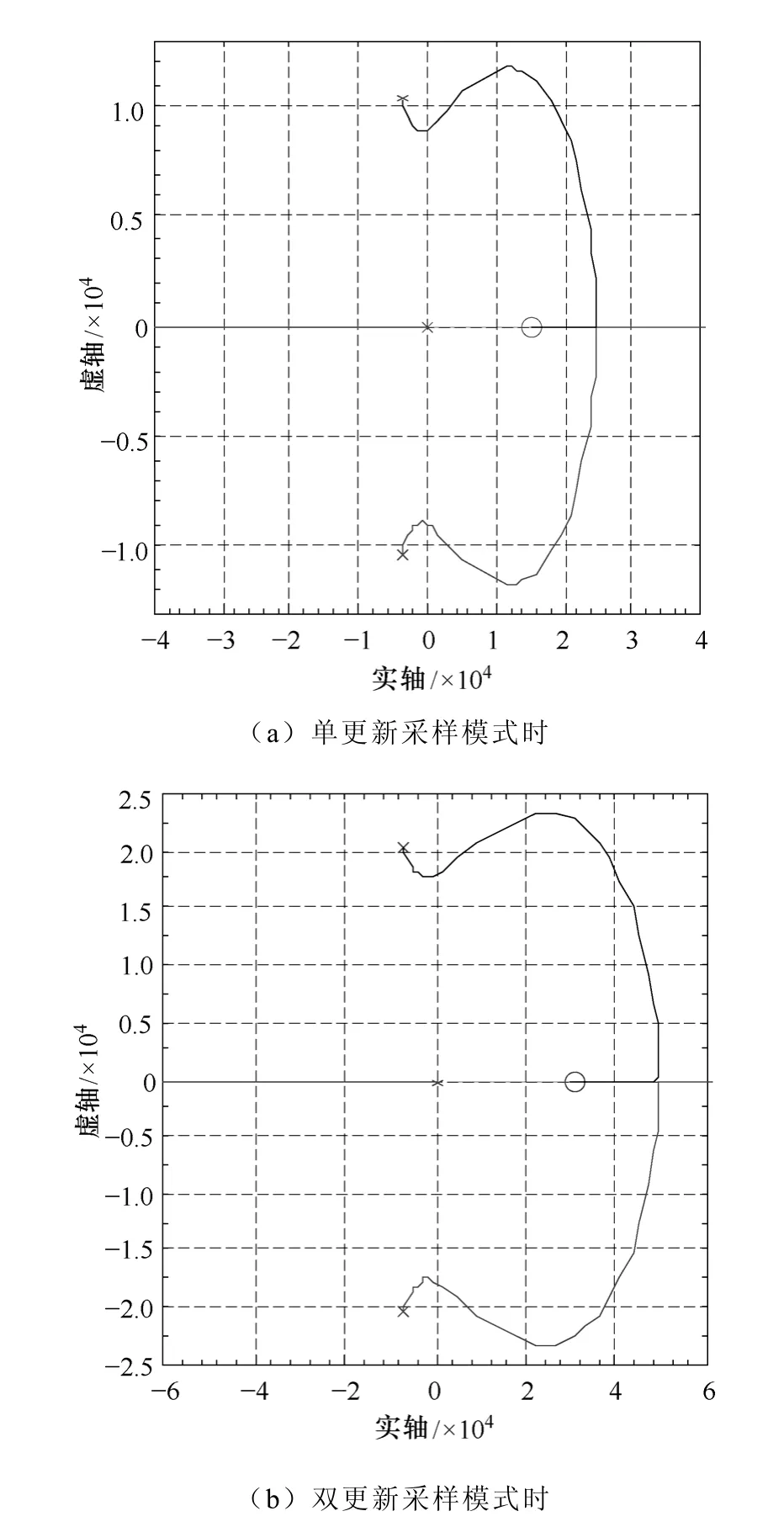
图5 外环根轨迹图 Fig.5 The outer loop root locus
在此基础上设计谐振控制器,谐振控制器需要确定K1的取值。采用谐振控制器时,K1越大,谐振点的开环增益越大,谐振控制器对临近区域的影响也越大。由于谐振点附近的相位有±90°的变化,所以根据频率特性图很难判定系统是否稳定。下面做出外环随K1变化时的根轨迹,由根轨迹可方便得到系统稳定时的K1取值范围。
fs取11.2kHz 和22.4kHz,对应的Ki分别取0.1和0.2,对应的Kv分别取1.1 和2.1,K1变化时外环的根轨迹如图6 所示。由图可知,单更新采样时,K1小于4.88×103时外环稳定;双更新采样时,K1小于2.33×104时外环稳定。两种情况下,分别选取K1为2300 和6000,这时阻尼较大,分别近似为0.13和0.43,超调最小,分别为66%和22%。
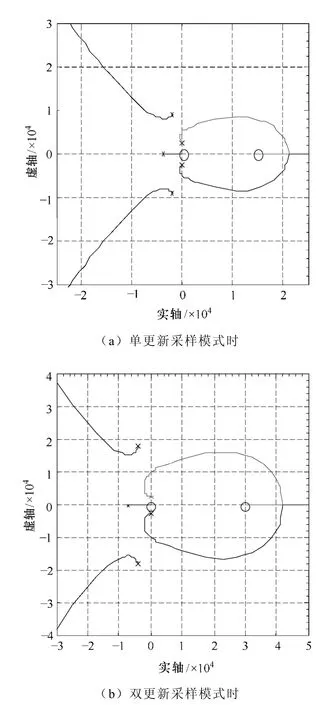
图6 K1 变化时的参数根轨迹 Fig.6 Parameter root locus when K1 changes
两种情况下的外环开环频率特性如图7 所示。Ho1 和Ho2 分别对应于单更新采样模式和双更新采样模式。可以看出双更新采样模式由于延时时间小,增益可以取得较大,带宽较宽。因此对于大功率400Hz/115V 系统,同样的开关频率,采用延时一拍控制时,采用双更新采样模式,可减小控制延时,使系统的动态和稳态性能好于单更新采样模式。

图7 开环频率特性 Fig.7 Open loop frequency characters
6 仿真和实验验证
6.1 仿真验证
按表1 所示参数建立仿真模型,单更新和双更新模式下的控制器参数见表2。

表2 控制器参数 Tab.2 The controller parameters
采用Tustin 方法对外环控制器进行离散化,两种采样频率下离散化的结果分别为
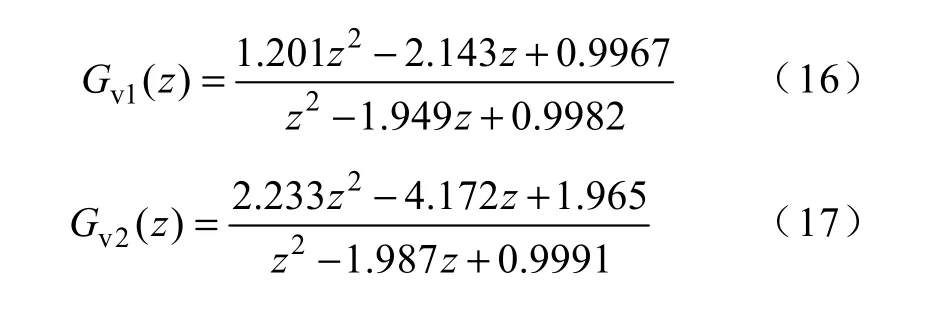
为了模拟数字执行时一个采样周期的延时,在内环引入一个单位延时,延时时间为一个采样周期。当负载为一个0.1Ω电阻和一个30μH 电感串联时,逆变器输出电压uo和参考电压波形ur如图8所示。因为双更新采样延时为单更新采样的一半,所以系统响应速度更快,稳态误差更小。单更新采样时需要近四十个基波周期系统才稳定,而双更新采样时只需三个基波周期,输出即达到稳定。由于采用了P+谐振控制,两种情况下的稳态误差都近似为零。
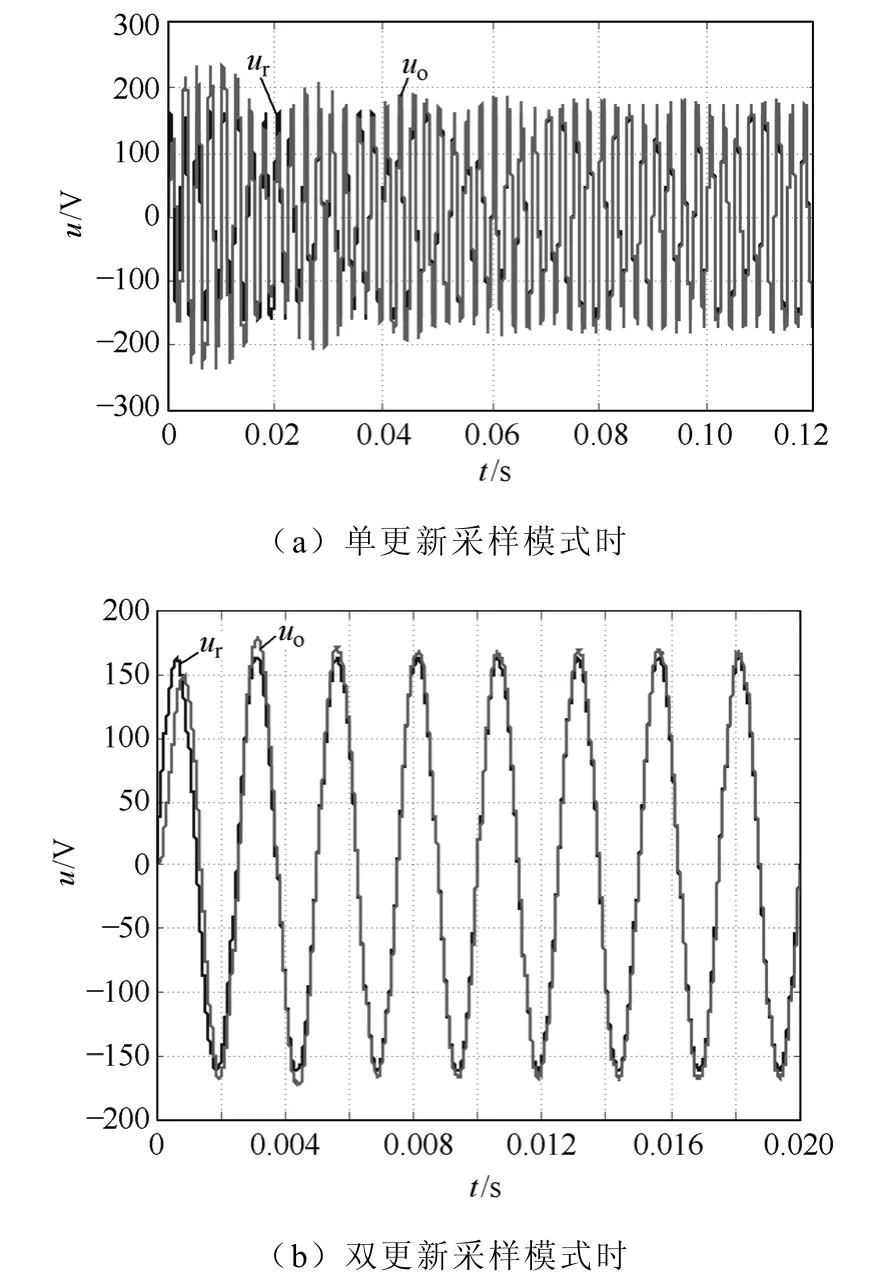
图8 输出电压和参考电压波形 Fig.8 Output voltage and reference voltage waveforms
6.2 实验验证
为了验证两种情况下的延时,利用DSP 和现场可编程序门阵列(FPGA),以同一个400Hz 正弦信号ur为参考,同时生成两种情况下的PWM 脉冲波形。采用DSP 发出频率f 为400Hz 的正弦参考信号,送到FPGA。FPGA 内产生四个相位互差π/2、频率fs为2.8kHz 的三角波。正弦波与三角波比较后产生相应的脉冲信号。通过 FPGA 的嵌入式软件SignalTap 直接采集FPGA 端口的脉冲信号,根据式(1)分别得到两种情况下的uT波形,如图9a 所示,可以看出双更新采样时的uT相对于参考波ur的滞后更小。用Matlab 对这三个波形数据进行分析,可得到参考信号与两种情况下uT基波的相位差,如图9b 所示,分别为(19.3±0.1)°和(9.6±0.1)°,与通过式(7)计算所得到的值一致,证明了延时分析的正确性。
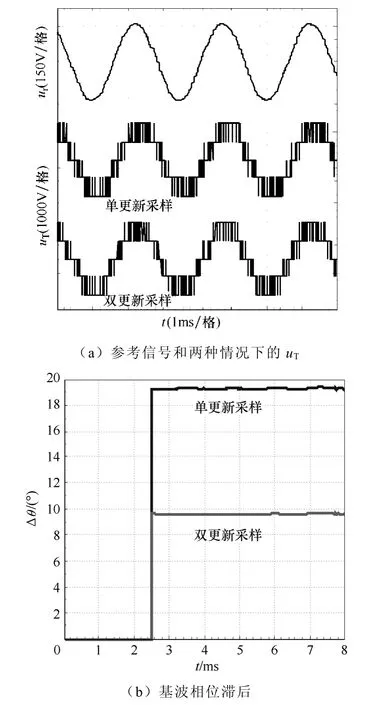
图9 单更新和双更新时的uT 波形及相位滞后 Fig.9 uT waveforms and fundamental lagging phases
7 结论
本文对大容量400Hz 逆变器采用延时一拍控制时的采样、计算和DPWM 延时进行了分析,采样、计算延时为一个采样周期,DPWM 延时近似为1/2采样周期。通过在连续域设计中引入等效延时环节的方法对数字控制参数进行了近似设计。由频域可知,延时时间越长,系统越不容易稳定,控制器参数取值范围越小。最后对一个100kVA 的400Hz/ 115V 逆变器进行了控制设计,建立其离散仿真模型,仿真结果证明了理论分析的正确性。通过DSP结合FPGA 的方法对单更新和双更新采样引入的延时进行了实验验证。
[1] Jensen U B,Blaabjerg F,Pedersen J K.A new control method for 400Hz ground power units for airplanes[J].IEEE Transactions on Industry Applications,2000,36(1):180-187.
[2] 蔡昆,李耀华,胜晓松,等.高性能单相电压源逆变器的输出控制[J].电工技术学报,2005,20(1):104-107.
Cai Kun,Li Yaohua,Sheng Xiaosong,et al.Output control of the high performance single-phase voltage- source inverters[J].Transactions of China Electro- technical Society,2005,20(1):104-107.
[3] 张纯江,张婧,邬伟扬,等.基于Delta 算子的谐振控制器实现高频链逆变器波形控制[J].电工技术学报,2008,23(7):81-85.
Zang Chunjiang,Zhang Jing,Wu Weiyang,et al.High-frequency link inverter waveform control with resonant controller based on delta operater[J].Transactions of China Electrotechnical Society,2008,23(7):81-85.
[4] 谢孟,蔡昆,胜晓松,等.400Hz 中频单相电压源逆变器的输出控制及其并联运行控制[J].中国电机工程学报,2006,26(6):78-82.
Xie Meng,Cai Kun,Sheng Xiaosong,et al.Output control and parallel operation control of 400Hz single-phase voltage-source inverter[J].Proceedings of the CSEE,2006,26(6):78-82.
[5] Mihalache L.Improved load disturbance rejection method for 400Hz GPU inverters[C].IEEE PESC,2004:95-101.
[6] 李建林,张仲超,许洪华.基于级联H 桥五电平变流器 SAPF 的应用研究[J].电工技术学报,2006,21(2):79-82.
Li Jianlin,Zhang Zhongchao,Xu Honghua.Research on SAPF based on cascade H bridge five-level converter[J].Transactions of China Electrotechnical Society,2006,21(2):79-82.
[7] 李建林,许鸿雁,高志刚,等.级联 H 桥五电平变流器工况分析与验证[J].电工技术学报,2007,22(4):85-91.
Li Jianlin,Xu Hongyan,Gao Zhigang,et al.Analysis and validation of cascade H-bridge five-level converter operating condition[J].Transactions of China Electrotechnical Society,2007,22(4):85-91.
[8] Zmood D N,Holmes D G,Bode G.Frequency domain analysis of three phase linear current regulators[J].IEEE Transactions on Industrial Applications,2001,37(2):601-610.
[9] Zmood D N,Holmes D G.Stationary frame current regulation of PWM inverters with zero steady state error[J].IEEE Transactions on Power Electronics,2003,18(3):814-822.
[10] Teodorescu R,Blaabjerg F,Liserre M,et al. Proportional-resonant controllers and filters for grid-connected voltage-source converters[J].IEE Proc.Electr.Power Appl.,2006,153(5):750-762.
[11] Liserre M,Teodorescu R,Blaabjerg F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J].IEEE Transactions on Power Electronics,2006,21(1):263-272.
[12] Heng Deng,Oruganti R,Srinivasan D.PWM methods to handle time delay in digital control of a UPS inverter[J].IEEE Power Electronics Letters,2005,3(1):1-6.

