工频磁场对电磁继电器动态特性影响的 三维有限元分析

杨文英 任万滨 翟国富 李岐新

(1.哈尔滨工业大学军用电器研究所 哈尔滨 150001 2.陕西群力电工有限责任公司 宝鸡 721300)

1 引言

电磁继电器在工业控制、现代通信等领域应用广泛，在执行控制、信号传递、系统配电等方面起着重要作用。作为基础的电器元件，研究其电磁兼容性能，对于提升整个系统的抗干扰能力和可靠性具有不可忽视的作用。

电磁继电器既是一种电磁干扰源，同时也是电磁干扰的敏感元[1-3]。外界电场、磁场的干扰，都会影响其动态特性，甚至导致其误动作，危及继电器控制系统的正常运行[4-7]。其中，工频磁场的干扰就是一种很典型的干扰形式。

工频磁场是由导体中的工频电流产生的，或者极少量的由附近的其他装置（如变压器的漏磁通）所产生。正常运行条件下的电流，产生稳定的磁场，幅值较小；但故障条件下的电流，则能产生幅值较高、持续时间较短的磁场。

本文采用三维有限元方法仿真分析了电磁继电器受到短时工频磁场干扰时的动态特性，给出了不同幅值的工频磁场对继电器动态特性的影响规律，并定量分析了继电器吸合时间、电磁力矩、衔铁吸合速度以及吸合电流的变化情况。本文的分析方法对研究继电器受到工频磁场干扰时的动态特性十分有效，对设计继电器时就考虑其抗干扰性能具有借鉴意义。

2 分析方法

2.1 研究对象的实体模型

分析的对象是典型的拍合式电磁继电器，其结构和相关尺寸如图1 所示。该继电器的主要尺寸如下：l1=6mm，l2=0.74mm，l3=10mm，h1=0.05mm，

h2=6.3mm，h3=4.66mm，h4=5.06mm，h5=0.74mm，

Φ1=3.78mm，Φ2=9.1mm。当继电器处于释放状态时，工作气隙δ =0.377mm，衔铁的转角θ =3.1°；当继电器处于吸合状态时，工作气隙δ = 0.02mm，衔铁的转角θ = 0°。

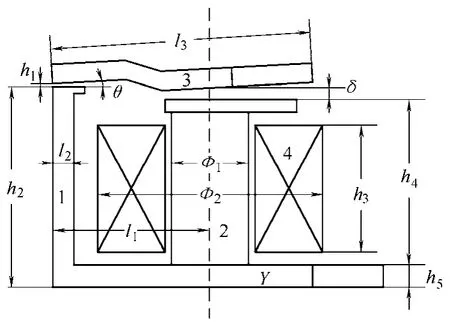
图1 电磁继电器的结构 1—轭铁 2—铁心 3—衔铁 4—线圈 Fig.1 Structure of electromagnetic relay

2.2 电磁场的有限元求解方程

电磁继电器的动作过程包含了电磁场的计算问题以及衔铁运动的动力学问题还有电路的计算，因此是一个十分复杂的磁、电、机械耦合求解问题，采用三维有限元方法进行建模分析，可以很好地对该问题进行求解[8-9]。

标量有限元法求解不含永磁的电磁继电器磁场的基本方程为

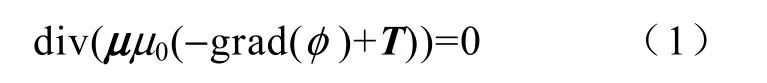
式中 μ—相对磁导率张量；

μ0—空气的磁导率；

φ —标量磁位；

T—激励源。

T 由线圈电动势或外磁场提供，采用标量线圈作为激励线圈时，可以通过毕奥-沙伐尔定理解析求解。

采用无限远边界条件，可较为真实地模拟出分析域的边界条件。通过有限元法求解出电磁场，得出线圈磁链，再由虚功法计算衔铁受力，得出其对转动轴的电磁转矩Tm。

2.3 机械运动方程

求解电磁场，通过虚功法计算得出衔铁的电磁转矩Tm，衔铁在此力矩的作用下，按式（2）所示方程绕其转轴进行转动。

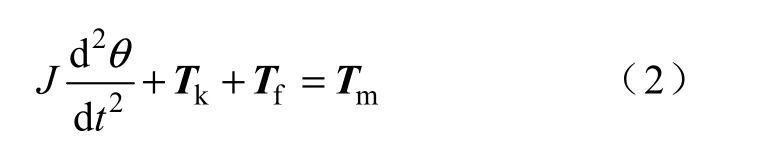
式中 J—衔铁的转动惯量；

θ —衔铁的转角；

Tk—弹簧反力提供的负载转矩；

Tf—摩擦力转矩。 由式（2），解出衔铁在下一时间点的位置角度θ，角速度ω以及角加速度β。

2.4 电路方程

通过电磁场的求解可得线圈磁链，再由磁链随时间的变化率和式（3）所示的电路方程，求解下一时间步的线圈电流。

式中 u—线圈激励电压；

R—线圈电阻；

i—线圈电流；

ψ —励磁线圈磁链。

3 仿真建模

3.1 继电器有限元模型

继电器的额定电压为12V，线圈电阻为280Ω，匝数为2100。采用三维有限元法建立的模型如图2所示。其反力特性如图3 所示。

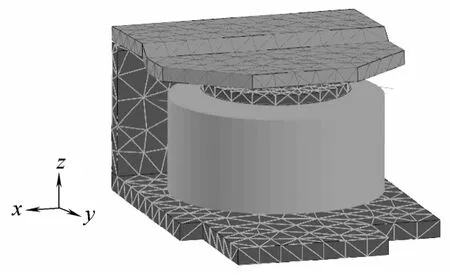
图2 有限元模型（隐去空气单元） Fig.2 FEM model of electromagnetic relay （air element is hidden）

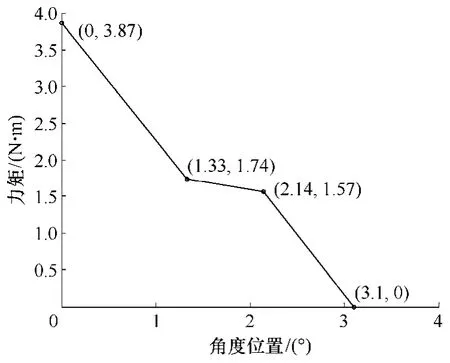
图3 反力特性 Fig.3 Load characteristic of the return spring

3.2 外部磁场干扰模型

采用通电长直螺线管来建立继电器外部的工频干扰磁场。以继电器上下对称平面和其铁心轴线的交点为坐标原点O，铁心轴线方向为z 轴，衔铁转动平面为yz 平面，建立直角坐标系xyz（见图4）。外部螺线管的中心位置位于原点O，当其绕x 轴转动时，转角设为α；当其绕y 轴转动时，转角设为β。设螺线管处于初始位置时，其轴线与继电器铁心轴 线重合，转动方向以逆时针为正，顺时针为负。当螺线管通以电流I，在其内部产生磁场，从而对位于其中心区域的继电器产生磁干扰。改变电流值I，可以改变继电器受到的干扰磁场的大小。改变电流方向，可以得到相反方向的干扰磁场。

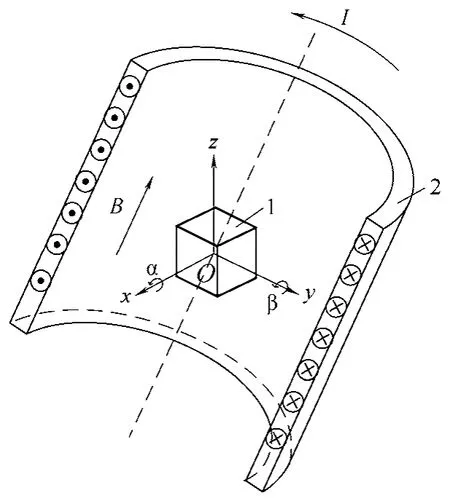
图4 工频干扰磁场模型 1—继电器 2—通电螺线管 Fig.4 Model of power frequency magnetic field

螺线管长度设为80mm，半径为35mm，匝数为83 766 时，得到其电流I 为0.01A，在内部中心区域生成 0.01T 的磁场。该中心区域大小为 20mm×20mm×20mm，可以将继电器完全包含其中。电流频率设定为50Hz，即可产生工频干扰磁场。

根据文献[10]对继电器受到外部恒定干扰磁场的分析，可知继电器受到磁场干扰的敏感方向，沿其铁心轴线。因此，在仿真分析的过程中，为了观察外部磁场干扰的最恶劣情况，沿继电器的轴线方向施加工频干扰磁场，同时假设磁场正方向沿z 轴正向。

4 仿真结果分析

本文主要分析研究继电器动作吸合过程。考虑当磁场处于负半周，相角为270°时，对继电器的吸合影响会较大。因此，假设继电器动作时刻，干扰磁场幅值为负向最大，如图5 所示。图中，5ms时刻，继电器开始动作。继电器实测的吸合时间约为2.7ms，因此，继电器的整个吸合过程都受到负向工频磁场的干扰。

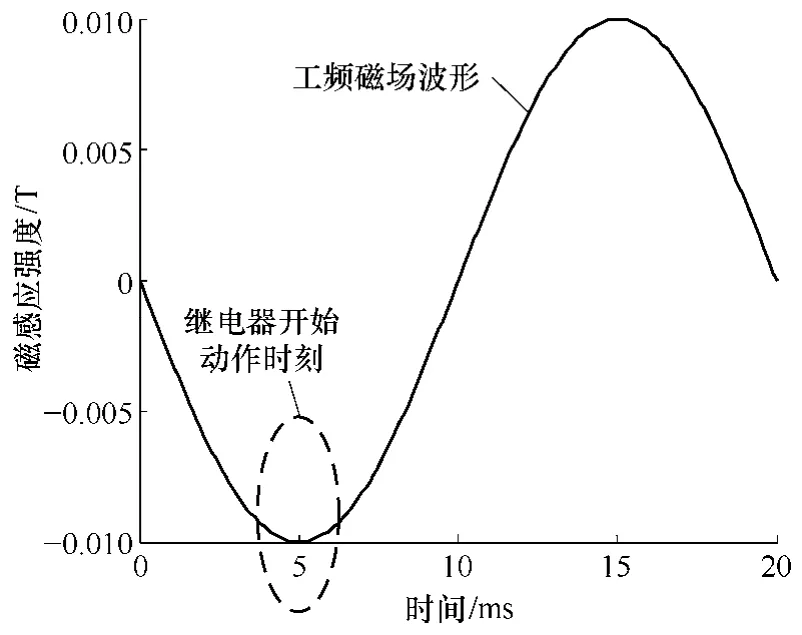
图5 继电器动作时刻与工频干扰磁场关系示意图 Fig.5 Relationship between operation time and power frequency magnetic field

4.1 继电器磁场分布图景

在继电器发生吸合动作前（即5ms 时刻），外部干扰磁场在继电器内的分布云图如图6 所示。改变干扰磁场的幅值，从0.01T 至0.04T，从图中可看到磁场分布的变化规律。

图6 磁场分布云图（5ms 时刻） Fig.6 Distribution of magnetic field in relay (at 5ms)

由图6 可知，当继电器处于释放状态时，衔铁和铁心之间的工作气隙为377μm，而衔铁和侧轭铁之间的距离仅为50μm，因此，该处的磁阻远小于工作气隙磁阻。所以，磁场主要分布在侧轭铁内部。而这样的磁场分布，直接导致外部干扰磁场会对继电器的衔铁产生一个干扰力矩，其方向同线圈产生的吸力力矩相反，从而会阻碍继电器的正常吸合。而且，随着磁场增大，继电器侧轭铁内的磁场从0.5T增大至1.5T 左右，产生的干扰力矩也更强。该干扰力矩随磁场幅值变化的关系曲线如图7 所示。从图7 中可以看出，干扰力矩随着磁场强度的增加，几乎呈线性增大的趋势。

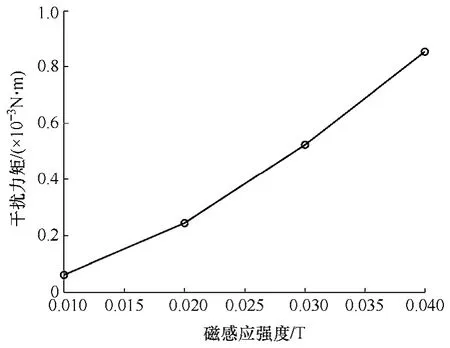
图7 干扰力矩随磁场变化曲线 Fig.7 Variation of interference torque with magnetic field

4.2 动态特性

动态特性反映继电器的动作性能，动态特性求解时间步长为 0.1ms，衔铁的转动惯量为 1.55×10−8kg·m2。衔铁在线圈产生的电磁吸力作用下，完成吸合过程，但由于其受到外部工频磁场的干扰，在干扰力矩的阻碍下，吸合时间会发生明显改变。不同大小的干扰磁场对继电器动态特性的影响，如图8 所示。吸合时间随磁场的变化曲线如图9 所示。 可以看出，吸合时间随磁场线性增加。当干扰磁场幅值达到0.04T 时，继电器的吸合时间约为5.8ms，是正常闭合时间的2 倍。

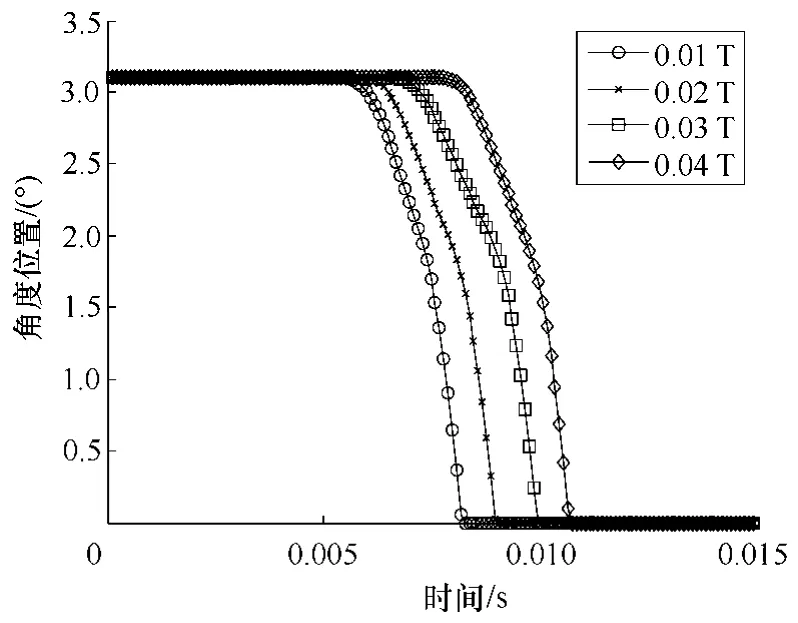
图8 继电器动态特性 Fig.8 Dynamic characteristic of relay

图9 吸合时间随磁场变化曲线 Fig.9 Variation of operation time with magnetic field

4.3 衔铁吸合速度

衔铁的吸合速度，是研究继电器动作过程的一个关键因素。闭合时速度越大，往往越容易发生回跳，从而产生吸合电弧，增加对继电器触点的烧蚀。因此，闭合时的速度并非越大越好。当外部干扰磁场增大时，衔铁在吸合过程中的速度曲线如图 10所示。衔铁闭合时的速度同磁场的关系曲线如图11所示。可以看出，衔铁闭合时的速度并非随着磁场的增大而一味减小，当磁场增大至0.04T 时，衔铁的速度反而增大。这主要是因为，磁场增大到一定程度，会使继电器的吸合持续时间超过工频磁场的1/4 周期，这样当继电器处于正半周的干扰磁场作用下，会加速其吸合，从而导致衔铁闭合时刻的速度增大。

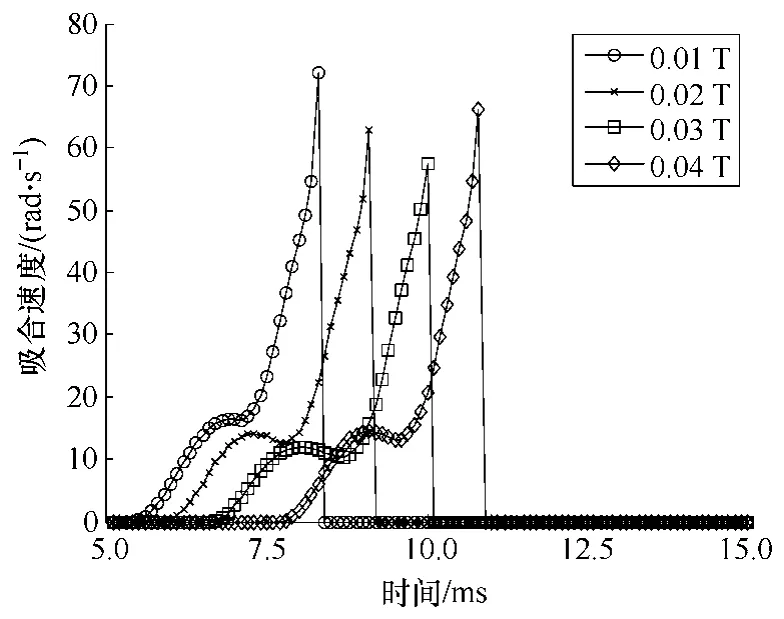
图10 吸合速度 Fig.10 Variation of pick-up velocity with time

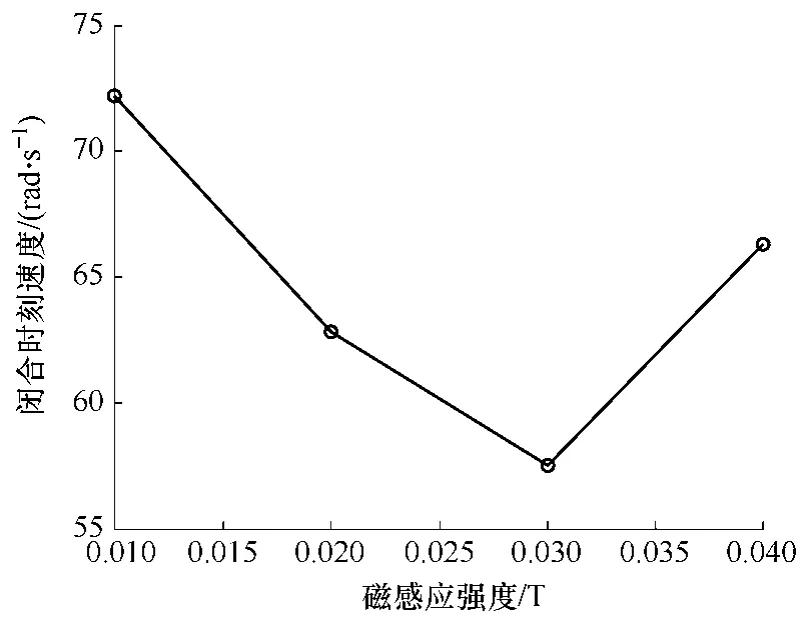
图11 闭合时刻速度随磁场变化曲线 Fig.11 Variation of pick-up velocity with magnetic field

4.4 吸合电流

继电器吸合过程中，线圈中的电流受外部磁场的影响规律如图12 所示。从图中可以看出，吸合过程中，无论外部干扰磁场大小，线圈中的电流都会在7.5ms 时刻上升到30mA 左右。但过了7.5ms，干扰磁场增大会导致电流下降至闭合时刻电流值的时间越长。而且，衔铁闭合后，磁场增大会使线圈电流达到稳态电流值的时间明显缩短。

图12 吸合电流 Fig.12 Coil current

5 实验验证

为了验证仿真结果的正确性，对继电器受到工频磁场干扰的情况进行了实验研究。实验原理框图如图13 所示。首先，由磁场发生器产生工频磁场，然后磁场的幅值可以通过高斯计测量得到，当磁场强度达到负向最大时，单片机系统控制继电器动作，同时发送启动信号给高速摄像机，拍摄下继电器受干扰情况下吸合过程。高速摄像机的拍摄速率设定为10 万张/s，分辨率为10μs。

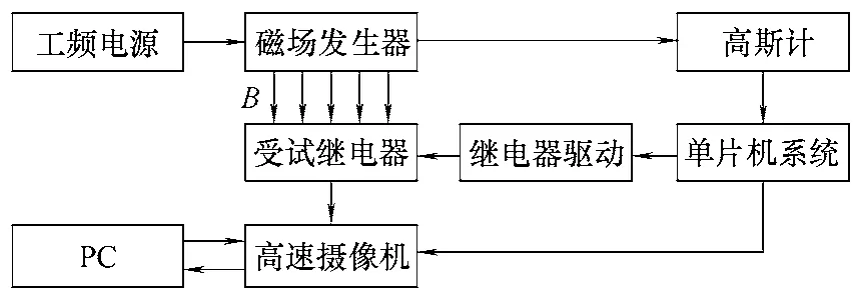
图13 实验原理框图 Fig.13 Block diagram of experiment

通过实验，得到在不同幅值的干扰磁场下继电器的吸合时间。同仿真计算结果比较，如图14 所示。可以看出，仿真结果同实测值较为一致，但随着磁场幅值增加，误差有所增大。

6 结论

外加工频干扰磁场时，采用三维有限元法对电磁继电器动态特性进行了仿真计算，并通过实验验证了仿真分析的正确性，得到结论如下：

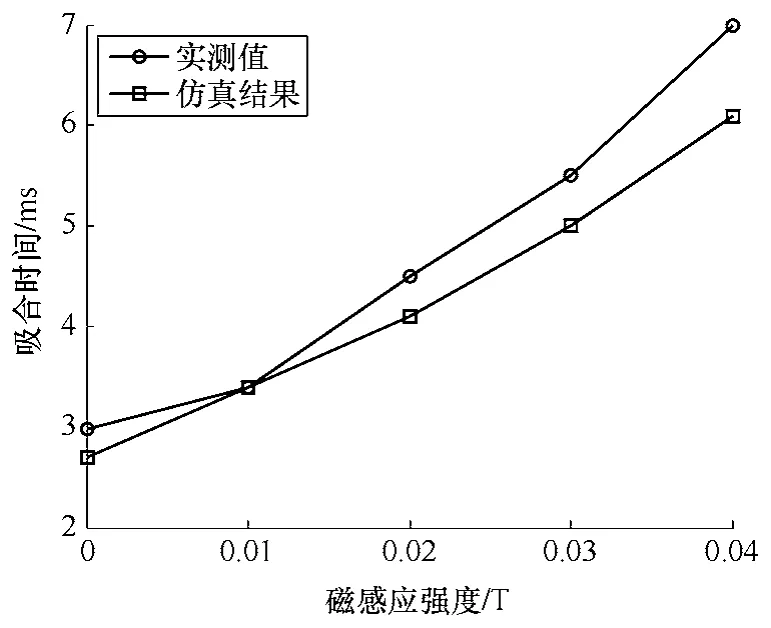
图14 实测吸合时间同仿真结果比较 Fig.14 Comparison of experiment and simulation

（1）当工频磁场处于负半周时，会对继电器的 衔铁产生干扰力矩，该力矩阻碍继电器的正常吸合，并且随磁场线性增加。

（2）继电器吸合时间受工频磁场影响显著，随磁场幅值增大，吸合时间明显变长。当干扰磁场幅值达到0.04T 时，吸合时间约为正常吸合时间的2 倍。而且，吸合时间也随外部干扰磁场线性增加。

（3）当磁场增大的程度不足以使继电器的吸合时间超过工频磁场的1/4 周期时，衔铁闭合时的速度呈递减趋势；而当磁场增大到一定程度，如0.04T，则导致继电器在闭合后半段会受到正半周的工频干扰磁场影响，从而增加了衔铁闭合时刻的速度。

（4）继电器吸合时，干扰磁场增大会导致电流下降至闭合时刻电流值的时间越长。而且，衔铁闭合后，磁场增大会使线圈电流达到稳态电流值的时间明显缩短。

[1] Minegishi S.Frequency spectra of the arc current due to opening electric contacts in air[J].IEEE Transactions on EMC,1989,31(4):342-345.

[2] Uchimura K,Fujita H,Ikesue S,et al.Noise induced by showering arc in switching relays and malfunction of digital circuits owing to its noise[C].IEEE International Symposium on Electromagnetic Com- patibility,Nagoya,Japan,1989,9:400-405.

[3] 李岐新,刘青.电磁继电器的电磁干扰现象及抑制方法[J].继电器,1998,26(1):51-57.

Li Q X,Liu Q.Electromagnetic interference of electromagnetic relays and the reduce method[J].Relays,1998,26(1):51-57.

[4] 黄道春,阮江军,余世峰,等.特高压紧凑型输电线路工频电场强度计算[J].高电压技术,2006,32(7):69-71.

Huang D C,Ruan J J,Yu S F,et al.Calculation of the power frequency electric field intensity of UHV compact transmission lines[J]. High Voltage Engineering,2006,32(7):69-71.

[5] 卢斌先,王泽忠,李成榕,等.500kV 变电站开关操作瞬态电场测量与研究[J].中国电机工程学报,2004,24(4):133-137.

Lu B X,Wang Z Z,Li C R,et al.Measurements and research of switching of switching operation transient electric field in 500kV substations[J].Proceedings of the CSEE,2004,24(4):133-137.

[6] Nils H,Dieter K.Overvoltages in secondary circuits of medium-voltage switchgear generated by multiple regnitions of circuit breakers [J].IEEE Transactions on EMC,1999,41(4):510-515.

[7] Hosaka H,Kuwano H.Design and fabrication of miniature relay matrix and investigation of electromechanical interference in multi-actuator[R].IEEE Workshop on Micro Electromechanical System,1994:313-318.[8] Kawase Y,Miyatani O,Yamaguchi T,et al.Numerical analysis of dynamic characteristics of electromagnets using 3-D finite-element method with edge elements[J].IEEE Trans.Magn.,1994,30:3248-3251.

[9] Yamaguchi T,Kawase Y,Shiomoto H,et al.3-D finite-element analysis of dynamic characteristics of twin-type electromagnetic relay[J].IEEE Trans.Magn.,2002,38(2):361-364.

[10] Zhai G F,Yang W Y,Zhou X.3-D finite element analysis of dynamic characteristics of twin-type relay interfered by uniform constant magnetic field[J].IEICE Transactions on Electronics,2008,91(8):1215-1221.