旋转测试树的多柔性体接触分析

刘敬花，胡桂川

LIU Jing-hua，HU Gui-chuan

（重庆科技学院 机械与动力工程学院，重庆 401331）

0 引言

接触问题出现在固体力学的许多领域中，并在机械工程和自然科学中有着广泛的应用。尽管接触与碰撞现象普遍存在，但接触力学至今还未能被充分认识。从工程的观点来看，接触动力学的理解和建模对产品设计以及提高产品性能和安全性非常重要。接触的处理非常麻烦却又非常重要，其算法不仅复杂，且计算时间也相当惊人。除了变形和波的传播外，接触的单向性导致的不等式约束乃为数学上难以处理的根本原因。

接触问题出现在固体力学的许多领域中，并在机械工程和自然科学中有着广泛的应用。尽管接触与碰撞现象普遍存在，但接触力学至今还未能被充分认识。从工程的观点来看，接触动力学的理解和建模对产品设计以及提高产品性能和安全性非常重要。接触的处理非常麻烦却又非常重要，其算法不仅复杂，且计算时间也相当惊人。除了变形和波的传播外，接触的单向性导致的不等式约束乃为数学上难以处理的根本原因。

长期以来，力学家和数学家一种致力于求解接触问题，研究过程可分为相互重叠的3个阶段[1]。第一阶段中只涉及刚体，用牛顿定律和欧拉定律来建立微分方程，摩擦用库仑定律描述；第二阶段以赫兹开创性论文[2]为标志，开始讨论弹性体的静态接触，描述如何计算接触区域和接触力，试图确定弹性体接触问题的解析解[3,4]，这些解析解虽然只局限于几何形体非常简单的接触问题，但这些研究非常重要，一方面是由于许多接触的物体可用简单的几何形体来进行近似

描述，另一方面是这些解析解可以用来检验数值计算程序；第三阶段是以数值计算为本，借助于计算机以及接触问题的近似处理，对复杂的几何形体和复杂的材料本构关系其接触过程进行数值模拟。

1 接触问题分析与数值求解

接触问题的特点是具有单侧边界条件和未知接触区域。接触区域与加载方式、荷载、接触面性质等密切相关，属于边界待定问题；材料的非穿透和接触力的不受拉即单侧边界条件是物体间的相对位置的约束条件。接触间的摩擦用库仑摩擦定律描述。接触问题的本质是非线性问题。

1.1 接触分析

在接触过程的计算中，根本性问题是如何满足非穿透性条件，不考虑物体自身的接触，物体间相互接触可用图1所示。

物体i（i=1,2,...,n）分别具有内部区域Ωi和边界

。在体力和面力的作用下，物体在空间中运动。在任意时刻每个物体的边界由给定位移的边界 、给定应力的边界 、接触边界 三个部分组成，即

非穿透性条件是指任意时刻任意物体内点不可能同时属于另一物体，即任意两区域的交集为空集：

图1 物体接触几何关系图

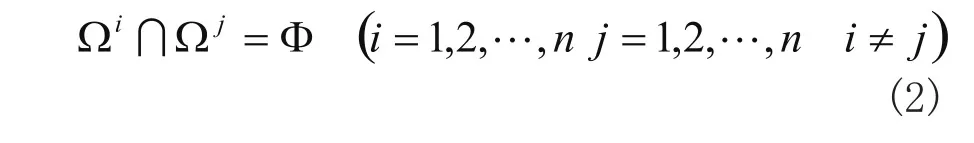
对于边界条件则有：

如图1所示，假设两个即将发生接触的物体上有最小距离的两个点P1和P2，物体具有光滑的外表面，物体上任意一点P可由该点在表面上的单位法向矢量和单位切向矢量，建立局部坐标系。若接触物体表面向外凸，则存在具有最小距离的两个最邻近点P1和P2。他们的局部坐标系坐标轴间有关系：

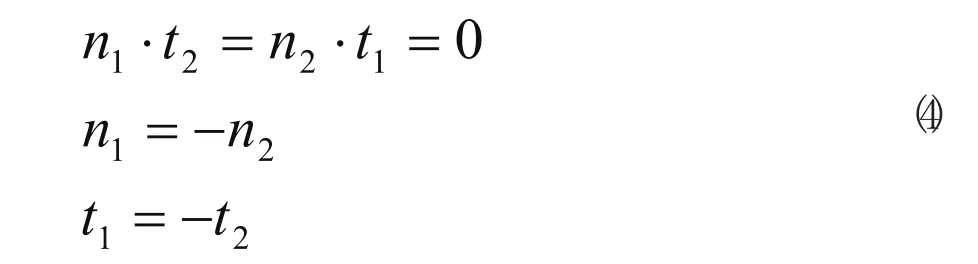
他们间的相对位移 与切向单位矢量正交，即：（5）

由最近点的相对距离g可以确定物体间最短的法向相对距离gN

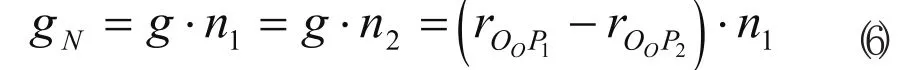
若gN＞0，则物体没有接触；gN=0，则物体相互接触；gN＜0，则物体相互渗透。

1.2 接触问题的数值解

数学上对施加无穿透约束的方法有拉格朗日乘子法、罚函数法和直接约束法。利用数值计算方法进行接触问题的求解流程如图2所示。

一些商品化的有限元分析软件提供了求解接触的专门分析工具。采用的方法有：

1）间隙单元 基于拉格朗日乘子或罚函数的接触界面单元；

2）非线性弹簧 基于罚函数方法，通过子程序施加非线性弹簧；

3）接触迭代法 直接约束的接触算法，是一种通用算法。对大面积接触，以及无法预知接触发生区域的接触问题，根据物体的运动约束和相互作用自动探测接触区域，施加接触约束。

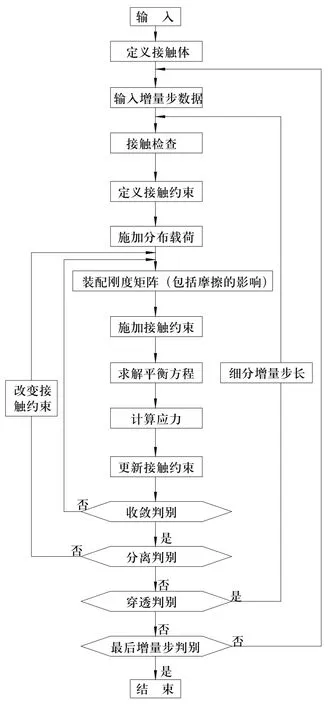
图2 接触算法流程图

2 测试树的接触分析

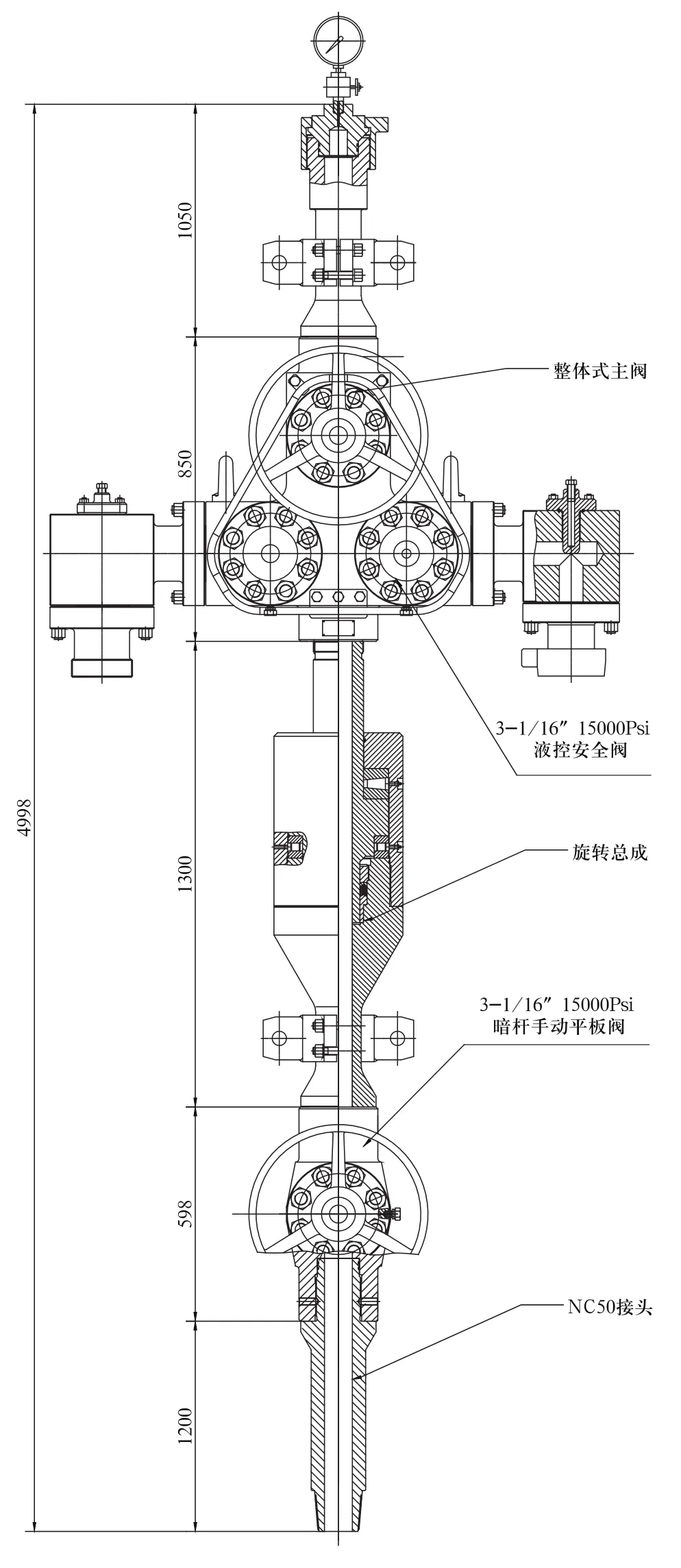
图3 测试树的结构图

如图3所示的测试树是石油钻井过程中，测量井下参数的一个关键设备，各个零部件间通过螺纹进行连接，测试树上端与采油树间通过螺纹连接。在设计工况下，流道内流动的介质为105MPa的泥浆，在NC50接头处连接的是钻柱，钻柱的重量为300吨。因此，测试树是在恶劣工况下、安全性要求非常高的设备。对螺纹连接区域的强度、测试树的整体结构是否满足现场的要求，是测试树设计过程中必须要解决的技术难题。利用有限元理论，研究测试树在设计工况下各个螺纹连接区域的应力、变形及其分布规律，提出优化方案具有非常深远的现实意义。

2.1 测试树有限元分析模型建立

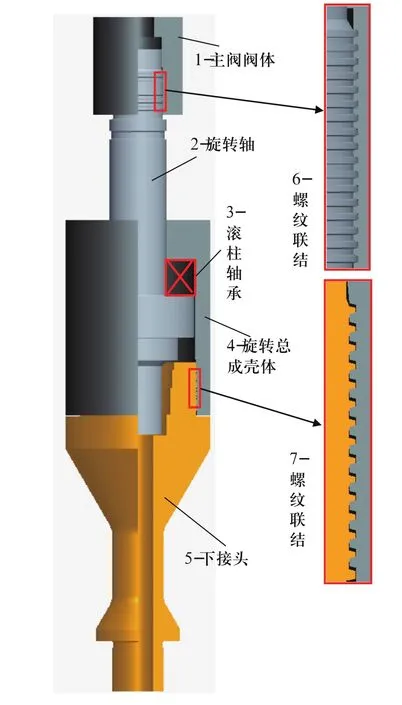
图4 测试树的三维实体装配图

测试树的所有零件均为回转体类零件，各个零件间通过螺纹进行连接。在进行有限元分析时，采用四节点的轴对称单元对回转体零件进行离散化，零件间的螺纹连接处忽略螺纹的升角，螺纹连接采用接触单一进行模拟。有限元分析模型如图5所示。

2.2 边界条件

测试树在工作过程中，其上端通过螺纹与采油树连接、下端与套管通过螺纹连接。进行测试树有限元分析的边界条件为：

1）约束条件 采油树断面约束；

2）载荷 作用在测试树的 载荷主要有测试树内部通道内泥浆的压力、钻杠的重量和测试树的重量。

1）泥浆的压力：105MPa；

2）钻柱的重量：按套管的最大最大重量300吨进行计算；

3）材料 测试树零件的材料为理想弹塑性材料。

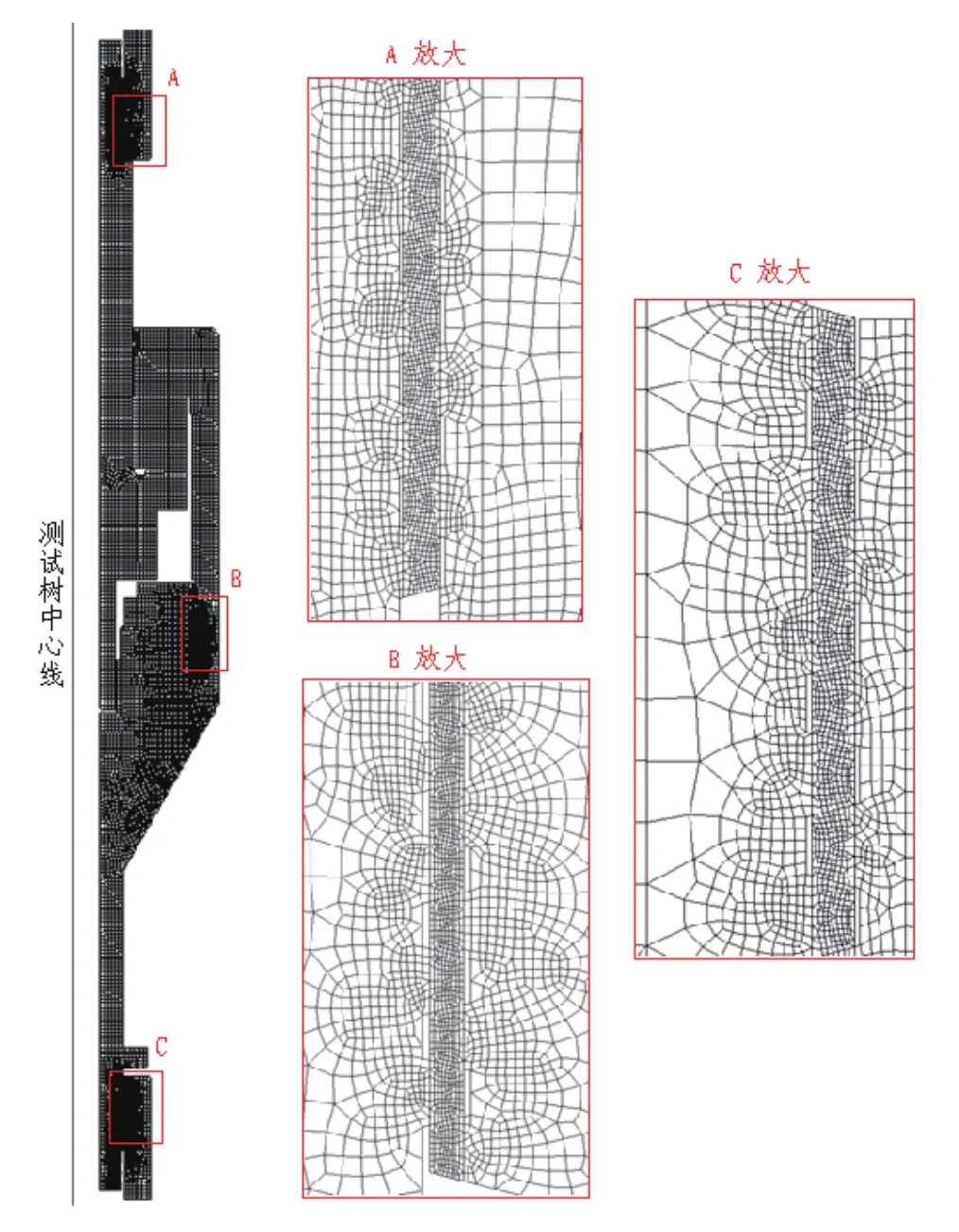
图5 测试树的有限元分析模型图

2.3 分析结果

对建立的模型，利用有限元分析求解器进行计算，获得给定边界条件下测试树的应力、变形及其分布规律。

从分析结果中可以得到下面结论：

1）测试树的最大变相为1.42mm，其变形较大，主要原因是测试树下接头最小段的壁厚较薄；

2）测试树的最大集中应力出现在螺纹连接区域，最大综合应力为556MPa，在阀体与旋转轴、下接头与套管的螺纹连接区域，测试树零件处于危险状态，应通过采用高强度的材料或改进结构的方法提高测试树的可靠性；

3）在各螺纹连接区域，螺纹的应力不均匀，在两端应力高、中间应力低，可以通过调整螺纹的连接长度实现螺纹应力的优化。

4）在旋转轴和下接头中，由于结构特征的突变，出现了应力集中，可以在两个突变特征间增加园角特征，降低集中应力。

通过有限元分析，为旋转测试树的结构优化提供了方向和理论依据。

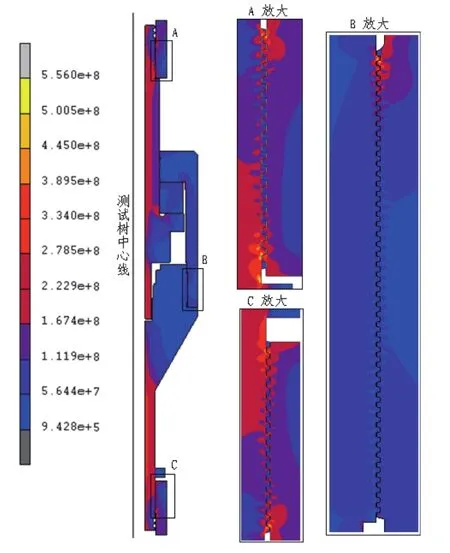
图6 测试树的综合应力分布

3 结论

1）研究了地面旋转测试树的多柔性体接触状况下的接触分析，开展了旋转测试树在套管载荷作用的弹塑性有限元分析。

2）采用有限元分析方法，进行了多柔性体接触仿真分析。分析结果表明，螺纹接触区域的应力分布呈非均匀变化，啮合螺纹的两端应力很高，中间部分应力较低，最大等效应力均出现在外螺纹接头根部及内螺纹端部，即位于内、外螺纹连接的最后啮合处；而螺纹接触应力的分布呈两头大、中间小的趋势。

3）通过地面旋转测试树的多柔性体接触分析，获得各个零件的应力、变形及其分布规律，为装配各个零件的结构优化提供理论依据。

4）本研究暂限于柔性回转体的轴对称四面体单元分析，但该多柔性体接触分析方法可以推广到三维多柔性体的接触分析问题中。

[1]彼得·艾伯哈特,胡斌.现代接触动力学[M].南京：东南大学出版社,2003.

[2]陈火红.Marc 有限元实例分析教程[M].北京：机械工业出版社,2002.

[3]傅衣铭,罗松南,熊慧而.弹塑性理论[M].长沙：湖南大学出版社,1996.

[4]张幼振,石智军,田东庄,等.高强度大通孔钻杆接头圆锥梯形螺纹的有限元分析及改进设计[J].煤炭学报,2010,35,（7）：1219-1223.

[5]刘巨保,丁宇奇,韩礼红.基于三维有限元模型的钻具连接螺纹上扣扭矩影响分析[J].石油矿场机械,2009,38（3）：28-32.

[6]高连新,金烨,史交齐.圆螺纹套管接头应力分布规律研究[J].机械强度,2004,26（1）：42-48.

[7]何敏,孙智.基于接触理论的高速精密压力机预紧力研究[J].机械工程学报,2010,46（11）：165-171.

[9]杨文玉.力抓取的接触力建模与可行抓取力分析.机械工程学报,2010,46（11）：43-48.