非均匀圆膜轴对称振动的离散模型的振动反问题

王其申，汪 杨，何 敏，钱华峰，刘全金

(1.安庆师范学院 物理与电气工程学院，安徽 安庆 246011;2.安庆师范学院 数学与计算科学学院，安徽 安庆 246011)

1 圆膜轴对称振动方程及其离散模型

考察质量轴对称分布的圆膜，其面密度只与半径r有关，即ρ=ρ(r)。这时圆膜振动方程成为:

这里y=y(r，θ，t)是膜的横向位移函数。考察最一般的轴对称边界条件:

其中:T与σ是正常数。对于这类轴对称膜的轴对称振动，膜的位移仅与径向坐标有关，y=y(r，t)。把方程(1)分离变数:y=u(r)ejωt，相应的径向方程成为:

这里ω是系统固有振动的圆频率。

一般而言，方程(3)已不是Bessel方程，但它显然仍为斯图膜-刘维尔型方程。上述方程在由式(2)经分离变量所得的边界条件:下，构成了较为特殊的一类斯图膜-刘维尔方程的本征值问题［1］。按照斯图膜-刘维尔方程的标准形式，这里的p(r)=rT，它在区间［0，a］的端点r=0处取零值，因而属于奇异本征值问题。相应地应有u(0)有界。由于这里仅考虑轴对称振动，进一步应有:

显然，对于一般的密度函数ρ=ρ(r)，特征值问题方程(3)～(5)没有精确解。为了寻求它的近似解，我们首先建立与方程(3)～(5)相应的差分离散系统。

图1 轴对称膜的差分格式Fig.1 The difference scheme of the axisymmetric circular membrane

引入差分点0=r0＜r1＜…＜rn=a并记lr=rs-rs-1(s=1，…，n)，这相当于把圆r≤a划分成一个一个的圆环，如图1所示。记fs、f's与f″s为相应函数在差分点rs(s=0，…，n)处的值，那么利用函数的精确到二阶小量的泰勒公式:

在略去高阶小量后，不难解出如下的二阶中心差分公式:

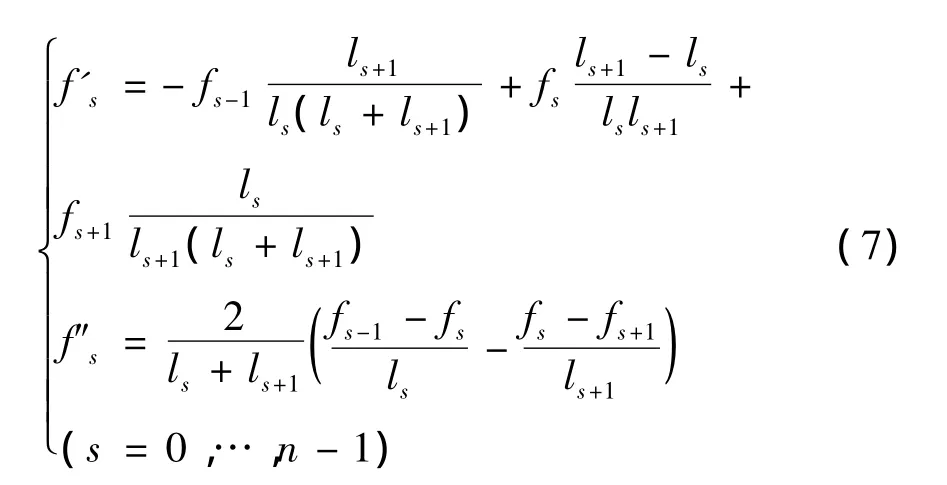
记us=u(rs)(s=0，…，n)。对于s=1，…，n-1 的内点，将上面的二阶中心差分公式(7)代入式(3b)有:

对s=n的端点处，直接利用泰勒展式(6)和边界条件式(4)得到:

以此连同泰勒展式(6)和边界条件(5)代入方程(3b)可得:

若引入变换:

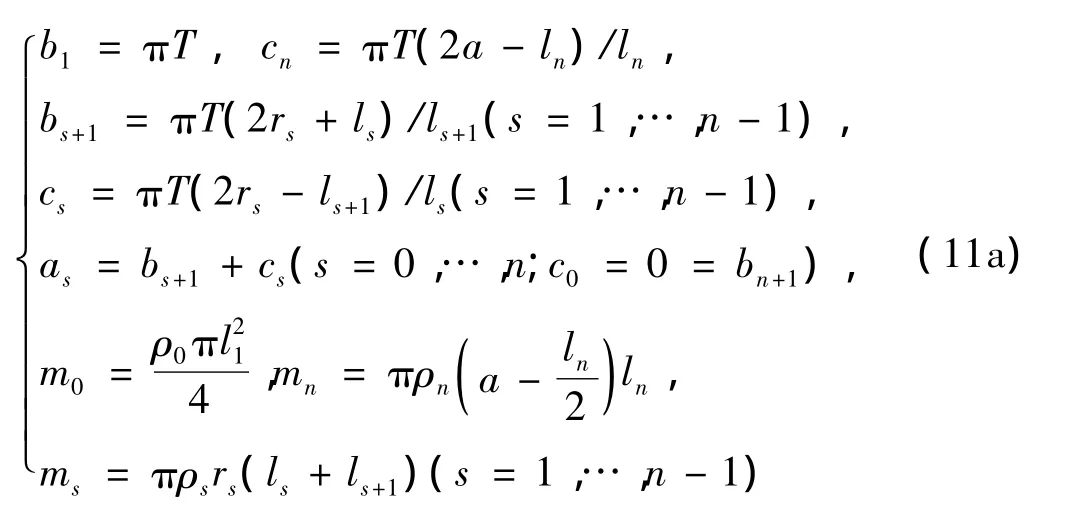
则上述离散后的方程成为:

这里:

代表边界力。可以看到，一般情况下这样导出的方程组并不是弹簧—质点系统的运动方程组.不过，所得系统仍然属于文献［4］中所定义的标准雅可比(Jacobi)系统。特别的，对于等步长的差分离散系统，l1=l2=…=ln=a/n，系数组(11a)简化为:

系统归于弹簧-质点系统。

2 圆膜离散模型的振动定性性质

鉴于上述差分离散模型属于雅可比系统，若记方程组(12)左边的系数矩阵为A，则用归纳法不难证明，当圆膜周边固定时，det A=b1b2…bn，而当圆膜周边弹性支承时，det A=b1b2…bnqn，从而除周边自由外，圆膜离散系统属于雅可比正系统。依据雅可比矩阵特征值和特征向量的特有性质［4］，我们马上可以得出轴对称膜的离散系统轴对称振动具有如下定性性质:

(1)系统的频率是实的和单的，可按从小到大次序排列为:

这里等号只在σ=0时成立。当0≤σ＜+∞时N=n+1而当σ=+∞时N=n。

(2)相应于ωk的第k个特征向量即第k个位移振型 u(k)=(u0k，u1k，…uN-1，k)T恰有k-1(k=1，2，…，N)个变号数。

(3)两个相邻振型 u(k)和u(k+1)(k=2，…，N-1)的节点相间。

(4)鉴于当σ=+∞时，膜的周边固定，un≡0。方程组(12)中的最后一个方程化为平衡方程。就是说，周边固定膜的离散系统的质量矩阵和刚度矩阵都是周边弹性支承膜的相应矩阵的截断矩阵。由雅可比矩阵与其截断矩阵的特征值的相间性推出，周边固定膜的离散系统频谱(k=1，2，…，n)和周边弹性支承膜的频谱(k=1，2，…，n+1)相间，即:

完全类似的也有:

(5)在式(13)中，注意到边界力Qn或边界力系数qn随表征边界支承弹簧常数σ的增长而增长，且qn≥0。若记=an+qn，显然有≥an且等号当且仅当σ=0时成立。就是说，周边自由膜的离散系统的刚度矩阵和周边弹性支承膜的相应矩阵的差别仅在于其右下角元素，而二者的质量矩阵是相同的，依据雅可比矩阵特征值与其元素之间的关系［4］可知，周边自由膜的离散系统频谱和周边弹性支承膜的频谱(k=1，2，…，n+1)也相间，即:

综上所述，更有

(6)导出周边固定膜的离散系统频谱和周边弹性支承膜的频谱相间关系的另一方法如下:

研究周边弹性支承膜的离散系统在其周边受一外力密度为q的简谐力作用时的强迫响应问题。这种情况下的强迫振动方程是:

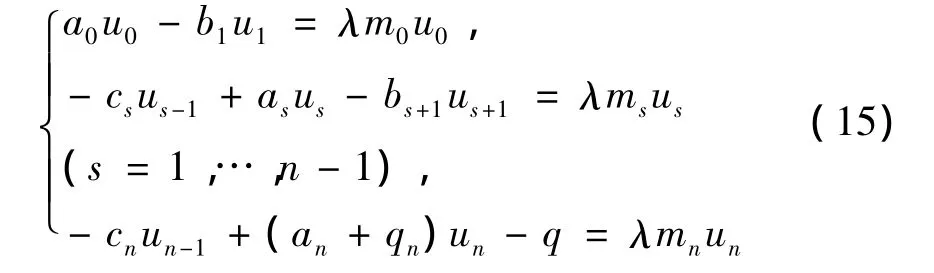
上述方程组写成矢量形式就是:

这里 λ = ω2，M=diag(m0，m1，…，mn)，e(n+1)=(0，…，0，1)T是n+1维列向量。

采用按固有振型展开的方法求解上述强迫响应问题，即设:

这里u(k)(k=1，…，n+1)是周边弹性支承膜的离散系统相应于固有圆频率的振型，

已经关于M归一化，即:

为了确定常数ck(k=1，…，n+1)，把级数展开式代入式(16)后两边再左乘矢量(u(k))T，即可解得:

于是，强迫振动的振幅向量可以表示为:

特别地，有:

从这里，我们得到周边固定膜的离散系统(un=0)的如下频率方程:

从这里，同样可以得出周边固定膜的离散系统频谱和周边弹性支承膜的频谱相间关系式(14)。

3 圆膜离散模型的模态反问题

与杆的纵振动的离散模型的模态反问题类似［5］，对圆膜的轴对称振动离散模型可以提出如下模态反问题:

给定周边固定或周边弹性支承膜的离散系统的两个模态(ωi，u(i))和(ωt，u(t))，这里 ωi＜ ωt，试确定系统的质量系数和刚度系数。

此式给出:

记:

则有:

不同于文献［5］的是，需要进一步计算周边弹性支承膜的离散模型的几何、物理参数.在给定ln、圆膜半径a和张力T的条件下，它们可按以下步骤计算:

(4)由于b1=πT是常数，由式(21)可得

至于周边固定膜，其模态反问题的提法和解法与周边弹性支承膜完全相似，只是减少一个自由度。

4 圆膜离散模型的频率反问题

提出并求解圆膜离散模型的如下频率反问题:

频率反问题的求解过程如下:

(1)由给定频率数据和式(18)可以解出周边弹性支承圆膜离散系统各振型的最后一个分量unk(k=1，…，n+1)。

(2)式(17)的第一式给出:

此式的对角元素给出:

由此可以解出mn。

(3) 令 q=M1/2u=(q0，…，qn)T，改写方程(12)为:

其中:

由此按照:

即可依次解出ci/mi和bi+1/mi(i=1，2，…，n)，这里bn+1=qn。继而仿照模态反问题算出差分步长lk(k=n-1，…，1)、弹性支承参数 σ 以及结点密度 ρk(k=n，n-1，…，0)。

5 反问题的计算实例

例1 周边固定的均匀膜，取n=10，ρ=1，T=1，a=1，采用等步长的差分格式。以相应的正问题的1、2阶模态为反问题的原始数据，计算相应的差分步长和结点线密度.计算结果列于表1。

表1 周边固定膜的模态反问题的数值计算结果Tab.1 The numerical calculated result on the inverse modes problem of membrane with the fixed boundary

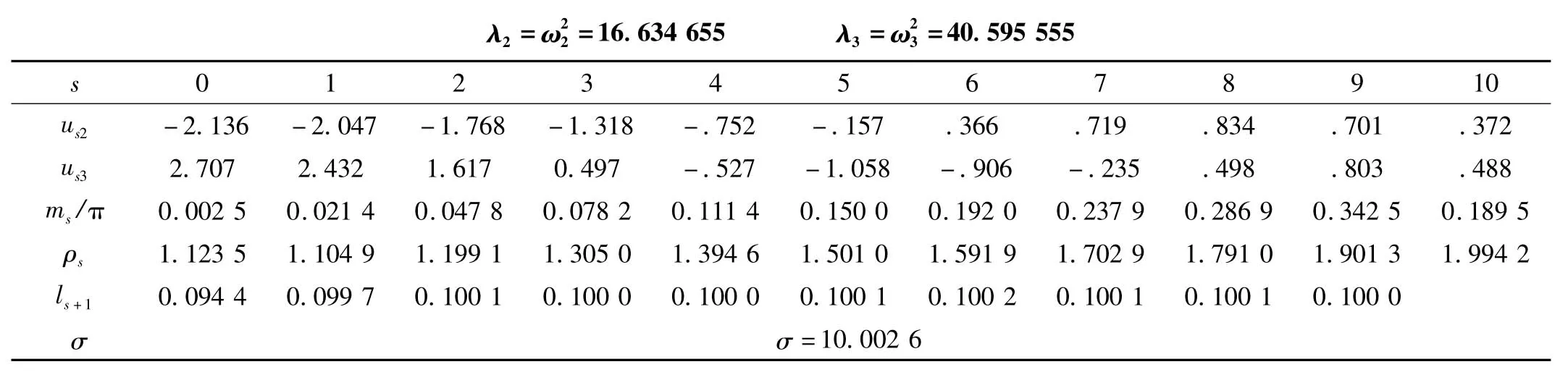
表2 周边弹性支承膜的模态反问题的数值计算结果Tab.2 The numerical calculated result on the inverse modes problem of the membrane with the spring supported boundary

表3 周边弹性支承膜的频率反问题的数值计算结果Tab.3 The numerical calculated result on the inverse frequencies problem of the membrane with the spring supported boundary

例2 周边弹性支承的变厚度膜，取n=10，ρ(r)=r+1，T=1，a=1，σ=10，采用等步长的差分格式。以相应的正问题的2、3阶模态为反问题的原始数据，计算相应的差分步长和结点线密度。计算结果列于表2。

例3 周边弹性支承的变厚度膜，取n=10，ρ(r)=r+1，T=1，a=1，σ=10，采用等步长的差分格式。以相应的正问题的频谱和周边改为固定时的频谱作为反问题的原始数据，计算相应的差分步长和结点线密度。计算结果列于表3。

6 结论

以上我们导出了轴对称圆膜做轴对称振动时所对应的差分离散模型，进而讨论了它的定性性质并求解了相应离散系统的振动反问题。以上算例表明，上述反问题的提法是合理的，反问题的解法是正确的。而且与文献［5-7］中的结论一样，频率反问题对原始数据的精度要求较之模态反问题要高得多。

［1］郭敦仁.数学物理方法［M］.北京:科学出版社，1982.

［2］余志祥，赵 蕾.张拉膜结构自振特性研究［J］.西南交通大学学报，2004，39(6):734-739.

［3］林文静，陈树辉，李 森，等.圆形薄膜自由振动的理论解［J］.振动与冲击，2009，28(5):84-86.

［4］甘特马赫、克列因著，王其申译.振荡矩阵、振荡核和力学系统的微振动［M］.北京:中国科技大学出版社，2008.

［5］王其申，王大钧.由部分模态及频率数据构造杆件离散模型［J］.振动工程学报(试刊号)，1987(1):83-87.

［6］何北昌，王大钧，王其申.Euler-梁的差分离散模型及其振动反问题［J］.振动工程学报，1989，2(2):1-9.

［7］吴 磊，刘全金，章礼华，等.外伸梁差分系统的模态反问题［J］.计算物理，2010，27(3):407-412.