复合作动器复合方式对平台主动隔振影响分析

陶 帅，白鸿柏，顾 伟

(1.63956部队，北京 100093;2.军械工程学院 自行火炮教研室，石家庄 050003;3.73906部队51分队，南京 210028)

微隔振平台在军工领域需要较宽的隔振频带和隔振的高效率，具有驱动、传感功能的压电驱动结构为微动平台主动隔振系统的建立提供了一种途径。致动器作为微隔振平台自适应控制的重要组成部件，它不仅具有结构承载功能，还具有驱动和传感的功能，压电主动元件研制成为发展自适应结构控制的关键问题之一。在Umland等［1］研制了低电压驱动的第三代主动元件后。在国内，芮小健等［2］对压电叠堆谐振特性进行了理论与实验研究;叶青等［3］开展了航天压电陶瓷致动器的设计与实验研究;李俊宝［4，5］研制了用于自适应桁架控制的主动元件;哈尔滨工业大学(威海)船舶工程学院张凯研究了一种新型的用于汽车发动机主动支承的压电液压驱动器［7］。作者在前述文献的基础上，研制出一种应用于压电微动平台的新型复合致动器［8］，为有效隔离平台外部扰动，研究了复合隔振元件物理参数对主动控制力的影响，为隔振元件的选择提供了依据。

1 隔振平台建模

1.1 复合压电作动器

未复合的压电陶瓷原件是由机械串联、电学并联方式粘结在一起的压电堆加上外围机械结构组合而成，其静力学模型可以简化成如图1所示的模型，即与弹簧刚度Kp并联，并受外力Fw作用。图中Fz为压电陶瓷由于受到电压控制和弹性原件及外力约束而产生的力，x为压电陶瓷作用位移。

图1 压电致动器等效力学模型Fig.1 The piezoelectric actuator's equivalent model

设压电陶瓷作用面积为A，长为L，弹性模量为E，压电应力常数为d33，压电陶瓷的自由位移:xz=d33u，则在外加电压u和预压力联合作用下，

式中Kz=EA/L。

由力学平衡条件得:

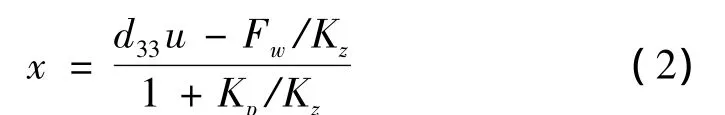
假设致动器上面驱动一质量为M的平台，建立动力学方程为:

式中Fz=Kzd33U，x0为平台地基扰动位移，c为作动器的等效阻尼，U为控制电压。

当未加控制力时的地基到平台传递率为:

由隔振基本理论可以知道，被控对象和外扰间直接加上一致动器后，由于致动器本身的刚度很大，相当于在被动隔振平台和地面之间联入了一刚性联结。与被动隔振系统相比，此时系统的频率比、阻尼系数将会降低，传递率大幅度提高。此时，即使加上了主动控制力，对整个系统而言，不仅耗散了不必要的能量，提高了驱动的压力，而且对隔振的效果而言，将会非常的不理想。为此，设计一种可以减小作动器等效弹簧刚度的致动器安装在系统中。

1.2 基于复合作动器平台的整体建模

复合隔振器由作动器和弹性体两种元件构成，弹性体可以用一个刚度和一个粘性阻尼来等效。根据其相对位置，复合隔振器可以有两种组合形式:作动器在弹性体下方、作动器在弹性体上方。干扰形式一般可分为空气、声音等的直接力干扰和通过地基传播的位移干扰。为分析作动器与弹性体不同组合方式下，针对不同类型干扰，对作动器要达到理想隔振效果所需要的控制力进行了标定。

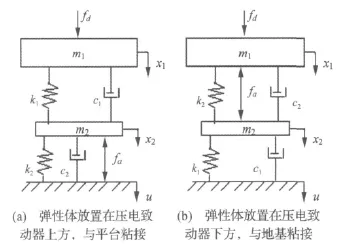
图2 弹性体和作动器相对位置简图Fig.2 The relative position of elastic solid and actuator

图1中m1为复合作动器的负载质量，k1、c1为橡胶的等效刚度和阻尼，忽略橡胶本身的质量，k2、c2为压电作动器的等效刚度和等效粘性阻尼，fa为作动器的输出力，x1、x2和u分别为负载和压电作动器等效质量及地面的绝对位移。

1.2.1 弹性体在上方

作动器平台系统的动力学方程为:

下标:1对应弹性体，2对应作动器，m2为致动器在其端点处等效的质量。

通过拉氏变换，如果隔振效果达到理想的X1=0，则上式可以变换为:

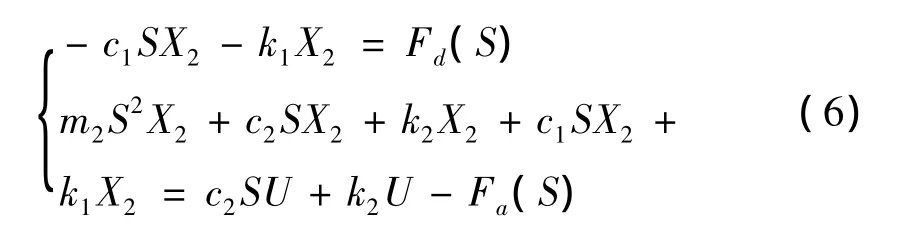
暂不考虑作动器本身的输出特性，就平台系统而言，要达到理想使隔振效果，要综合可虑直接扰动和地基扰动对平台的影响，才能决定致动器的输出力大小。由于两种扰动的互相独立性，可分开分析，然后通过综合，就能得到要达到平台隔振目的所需要的致动器输出力大小。

仅考虑直接干扰情况:即U=0，代入方程可得:

该表达式是在直接干扰下，平台中致动器的传递函数。也可以理解为:隔离单位直接扰动所需要的致动器输出。

仅考虑地基位移干扰时，即Fd(S)=0时，如果没有采取隔振措施，则基础对隔振对象m1产生的惯性力为:

拉氏变换为:

代入方程(6)可得:

同理，该比值可以理解为:要隔离单位地基扰动所需要的致动器输出。

对于传递函数，我们可以提出另外一种解释:对于单位(幅值)输入所引起的输出(幅值)或目标响应大小。针对上述作动器输出与不同外扰(地基扰动和直接干扰)的传递函数，其分别可以认为是:如果要抑制单位地基扰动或单位直接干扰需要的控制力。所以，针对隔振系统可能面临各种水平的地基扰动和直接干扰，可以用抑制α个单位直接扰动和β个单位地基扰动所需要的控制力(幅值)来评价传递函数对应系统的优劣。定义:

1.2.2 弹性体在下方

当弹性体放置在压电作动器下方时，由于橡胶的质量可以忽略，所以可以使m2=0，此时的m2是一虚质量(质量可以忽略)，且m1=um1+m1=(1+u)m1。致动器平台系统的动力学方程为:

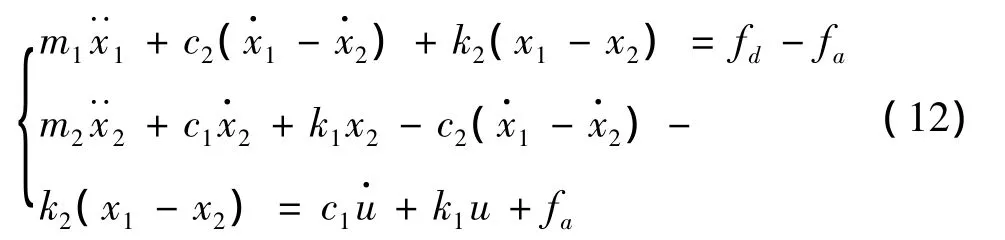
通过拉氏变换，如果隔振效果达到理想的X1=0，则上式可以变换为:

仅考虑直接干扰情况:即U=0，代入方程可得:

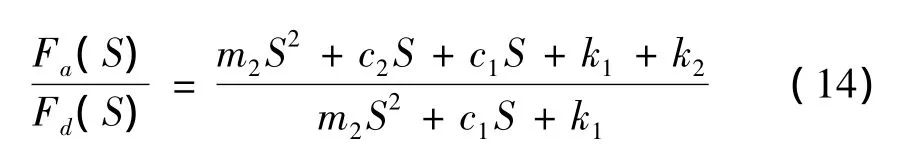
仅考虑地基位移干扰时，即Fd(S)=0时，代入方程可得:

同样用公式(11)定义此时系统的评价函数。

2 弹性体位置对控制力的影响仿真

在对两种安装方式进行仿真研究时，设作动器的等效质量与平台的质量比可以设定为1∶100。整个作动器的已知参数有:Kp=100 N/μm，Ks=1.818 N/μm，k2=Kp+Ks=101.818 N/μm，m1=50 kg，c1=2 119 N·s/m，m2=0.5 kg，k1=2.243 606 N/μm。

a代表直接干扰对平台系统施加力的单位数，b代表地基扰动对平台施加位移单位数。

图3 平台在直接干扰下作动器输出力幅比Fig.3 The platform's force translation rate in directly distrubation

图4 平台在地基干扰下作动器输出力幅比Fig.4 The platform's force translation rate in ground distrubation

图5 平台在混合干扰下作动器输出力幅比Fig.5 The platform's force translation rate in ground and directely distrubation

从图3可以看出，平台受不同类型干扰时，安装方式的不同，在不同的频段，隔振需要的作动器的输出也会有所不同。随着干扰频率的增加，在g＜1.42之前，作动器下方放置弹性元件，有利于降低作动器隔振控制力。由于ω2值本身较大，且微隔振平台主要隔振频率在低频段，因此，对于g＞1的部分不是关注的重点，这里不予分析。

从图4可以看出，当系统仅受单位地基扰动时，橡胶的位置对作动器输出控制力的影响基本一致。同时，为隔离单位地基扰动作动器所需要输出的控制力较隔离单位直接扰动所需要的控制力低一个数量级。因此，在选择作动器与橡胶放置位置时，需要考虑平台实际应用环境中，直接干扰力和地基扰动的(幅值)大小。

当平台系统受混合扰动时，分别取α=1～10，β=1～10进行仿真，整体趋势与图5的规律都相同(图5为α=10，β=1时的仿真图)，综合比较可以看出:橡胶放置在作动器的上方，如果要达到理想的隔振效果，在低频段需要的控制力要低于橡胶放置在作动器下方的情况。

在对平台进行主动控制时，复合压电作动器中橡胶和作动器位置的选择，除了上述理论分析的原因外，还考虑了作动器质量的等效方式对平台控制的影响。作动器虽然在整个平台系统中的质量基本可以忽略不计，但现实中存在这种等效质量。如果采用下方用弹性体与地面相接触，则在作动器质量等效时，可以将该质量等效到平台整体质量的一部分，此时，如果作动器支撑平台位置不对称，就会导致本就不确定的平台重心偏移，影响平台系统的耦合度，进而增加平台控制的难度;同时平台质量m1的变化，将导致作动器直接驱动时平台系统的固有频率，从而导致仿真曲线时横坐标g的偏移，使复合隔振系统的弹性体刚度和阻尼设计产生误差，得不到较优化的弹性体刚度和阻尼。如果采用作动器与地基相连，作动器质量可以忽略不计，又由于作动器的刚度很大，可以认为是地面与平台系统的一个刚性连接，以上偏差就不会产生。综合理论分析和上述原因选择橡胶放置在作动器的上方来构成复合压电作动器。

3 实验研究

本文根据上述分析，设计了复合压电作动器，将其应用到微隔振平台中，并设定平台的隔振效果指标为:使平台扰动位移峰值衰减80%。在白天，利用100 Hz采集一组地基扰动信号，其频率范围在1 Hz～20 Hz之间，采用状态反馈的鲁棒性能控制器对微动平台进行控制［9］，控制频率为 100 Hz。

弹性体在作动器上方时，设计出的状态反馈控制器u=kx的比例系数为:

弹性体在作动器下方时，设计出的控制器系数为:

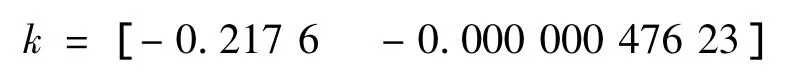
其控制效果如图6。

图6 平台信号Fig.6 Signal of platform

对平台控制10 s，结合实际控制环境，仿真地基扰动和直接扰动比值在5∶1到10∶1时的情况，比较不同复合作动器在达到相同的控制效果时所输出的控制能量比。从仿真的结果发现，在同样的外扰下，弹性体在下的布置如果要达到弹性体在上时的控制效果，其耗费的控制能量至少要多5%，且当平台受单一频率外扰时，在g=0.8时，其多耗费的能量达到了将近15%。

4 结论

通过分析复合压电致动器中致动元件和弹性元件不同位置对平台隔振控制力评价函数的影响，从仿真结果可以得出如下结论:弹性体放置在压电元件的上方时，可以有效隔离直接干扰对平台的扰动，且对平台动力学方程中的参数影响较小;弹性体放置在压电元件下方时，与弹性体放置在压电元件上方时抑制地基扰动所需要的控制力无明显区别。从作动器不同设计方式对平台控制效果的影响来看，弹性体在上方布置与其布置在压电材料下方，达到相同的控制效果所耗费的控制能量要少，且弹性体布置在上方更有利于隔离对平台影响较大的直接干扰量。

［1］ Umland J W，Chen G S.Active member vibration control for a 4 meter primary reflector support structure［A］.Proceedings of 33rdAIAA SDM Conference［C］，1992.

［2］芮小健，钟秉林，颜景平.压电叠堆谐振特性的理论与实验研究［J］.压电与声光，1993，15(2):42-46.

［3］叶 青，阎绍泽，汤晓瑛，等.压电主动元件设计与实验研究［J］.机械科学与技术，2003，22(4):629-631.

［4］李俊宝.智能桁架结构设计、建模与阻尼控制的理论和试验研究［D］.南京:南京航空航天大学，1996.

［5］李俊宝.压电作动器研制及其在空间结构振动控制中的应用研究［R］.博士后出站报告:西安交通大学，1998.

［6］严 蔚.智能主动构件的设计、分析和研究［D］.杭州:浙江大学，2004，

［7］张 凯，温建民.基于压电液压驱动器发动机主动支承系统的研究［J］.机械设计与制造，2009，10:97-99.

［8］陶 帅，白鸿柏，侯军芳，等.基于压电致动器的微动隔振平台系统［J］.振动与冲击，2010，29(3):147-149.

［9］侯军芳，白鸿柏.基于Riccati不等式的微动平台鲁棒性能控制器设计［J］.振动工程学报，2009，22(4):340-344.