基于改进的EMD方法提取车辆-轨道垂向耦合系统动态特性
陈双喜,林建辉,陈建政
(西南交通大学 牵引动力国家重点实验室,成都 610031)
轮轨系统的激励可以分为脉冲型、谐波型和动力型,由车辆和轨道两方面的因素造成。车辆方面较为单一,主要是车轮擦伤、车轮踏面几何不平顺及车轮偏心。而轨道方面的因素比较复杂,大体包括三个方面[1]:①轨道几何不平顺,如高低、水平、方向不平顺以及轨面的波浪形磨损;②钢轨接头不良;③轨下基础缺陷。轨面波浪型磨损是钢轨沿纵向表面出现的周期性波浪性不平顺,一般波长在25 mm~1 500 mm,波深0.1 mm~2 mm,其产生机理至今不明[2-4]。轨道的几何不平顺包括静态不平顺和动态不平顺,一般用多谐波函数表示[5]。由于轨道不平顺、波浪形磨损等因素的影响,高速列车运行时轮轨间将产生接触振动,甚至导致高频共振,对车辆和轨道使用寿命影响极大。通过动力学仿真计算出各种不同激励模型下的动力学响应,国内外学者对此进行了大量的研究,但是对复杂激励模型下车辆-轨道耦合系统动力学响应的动态特性提取主要以频谱分析为主,研究并不深入。而此方面的研究有助于对车辆-轨道系统动力学特性及其成因进行深入了解,具有重要的研究意义。
本文提出利用一种改进的经验模态分解方法对车辆-轨道垂向耦合系统的振动响应进行经验模态分解,提取耦合系统的各种动态特性,并且对垂向轮轨接触力、转向架和车体的加速度本征函数(IMF)进行了分析和比较,取得了较好的效果。
1 改进的EMD算法
经验模式分解(EMD)是美国华裔科学家Huang提出的新的信号时频分析方法。它将信号自适应地分解为多个本征函数(IMF)及一个余项,从而反映信号的内部特点。满足这样两个条件的信号称为本征函数(IMF):① 在整个数据序列中,极值点的数量(包括极大值点和极小值点)与过零点的数量必须相等,或最多相差不多于一个;②在任一时间点上,信号局部极大值确定的上包络线和局部极小值确定的下包络线的均值为零。EMD方法对非平稳、非线性信号处理具有较高的效率,但其局部均值的精度较低,计算速度较慢。此外EMD方法在对非平稳信号进行分解时,在数据的两端还会产生发散现象,并且这种发散的结果会逐渐向内“污染”整个数据序列而使所得分解结果严重失真(端点效应)。因此,有两个问题需要解决:一是如何进一步提高局部均值的求解精度,二是如何有效地消除因边界不连续而产生的边界效应。
在EMD方法中以局部极大值与极小值的包络线的均值代替信号局部均值并不是唯一的方法,其他求解方法有[6,7]:自适应时变滤波法(ATVFD)、极值域均值模式分解法(EMMD)、改进的极值域均值模式分解法(IEMMD)等。本文以改进的极值域均值模式分解方法来提高局部均值的求解精度。其步骤如下:
① 求出原始数据x(t)中所有局部极值点组成极值点序列e(ti),其中i=1,2,3…k。按照公式(1)计算出两相邻极值点间的局部均值序列mi:

② 假设mi在原始数据x(tii)与x(tii+1)(1≤ii≤k-1)之间。按式(2)求得mi对应的时间tγi:

③ 用两个相邻的局部均值mi(tγ1)和mi+1(tγ2)加权平均求ti+1处极值点的局部均值m(ti+1),即:

公式(3)中的k(ti)和k(ti+1)是通过相似梯形得到的加权系数,即:

求得极值点处的局部均值之后,就可以用这些点来拟合数据的局部均值曲线,进而分解出IMF。
目前已经提出了一些抑制端点效应的方法[6-9]:如采用神经网络对数据延拓法、在端点处按照端点数据变化的“平衡位置”附加两条平行线段的方法、极值点延拓法、基于AR模型的时间序列线性预测方法等。边界波形匹配预测法[10]能最大限度地维护原始信号在端部的变化趋势,相对与其它方法而言,其构造的虚拟极值点更加合理,对端点效应的抑制效果更加理想。考虑到计算的精度与成本和适应性,本文以边界波形匹配预测法来抑制端点效应。其基本步骤如下:
① 分别确定数据x(t)左右端的两个相邻极值点。假设左端两个极值点为e0和e1,右端极值点为en-1和en,左端点到e0这段波形记作w0,长度为l0,右端点到en-1这段波形记作wn,长度为ln。
② 计算整个数据段每一个极值点附近与w0(wn)长度相同的一段波wi与w0(wn)的匹配度mati。

s(j)表示波w0(wn)所有数据点,u(j)表示波形匹配计算中wi平移后的波形,N为序列长度。
③记mat=min(mati),如果mat<αl(其中α是一个常数,l为波的长度)则选取wi作为原始数据的延拓,否则选取原始数据两端的两个相邻的极值点的均值为两端的极值点。
2 车辆-轨道耦合动力学模型
车辆-轨道垂向耦合动力学模型如图1所示,包括车辆模型、轮轨耦合模型、轨道模型。其中轮轨耦合模型采用赫兹非线性接触理论实现车辆系统与轨道系统的耦合,其计算方法见文献[1]。
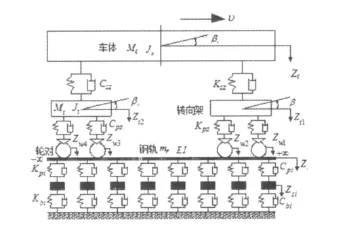
图1 车辆-轨道耦合系统模型Fig.1 Model of vehicle-track coupling system
2.1 车辆模型
本文建立10自由度客车垂向振动模型,包括车体和转向架的沉浮与点头、轮对的沉浮。车辆系统的振动响应微分方程为:

2.2 轨道模型
对于轨道系统的模型,本文选取弹性支承块式无砟轨道作为研究对象。文献[11]计算得知,钢轨的剪切变形和转动惯量对钢轨的固有频率有影响,模态越高,影响越明显。对于高速高频激励响应,只有钢轨采用Timoshenko梁模型,考虑钢轨断面的剪切变形,才能真实反映轮轨系统的高频振动。为了满足高速高频振动要求,本文选取钢轨模态阶数为NM=90,钢轨长度为120 m。于是,钢轨模型微分方程[11]为:

式中,A为钢轨断面面积;mr为单位长度钢轨质量;E为钢轨弹性模量;I为钢轨截面惯量;k为钢轨截面影响系数;Φr(x,t)为钢轨轴线的转角;zr(x,t)为钢轨的振动位移;G为钢轨剪切模量;Fj为轮轨作用力;Ri为支承块反作用力。
弹性支承块的振动微分方程[1]为:

式中,Msi为弹性支承块质量;Zsi为支承块位移;Kbi、Kpi为块下胶垫和扣件的刚度;Cbi、Cpi为块下胶垫和扣件的阻尼。
2.3 轨面激励模型
对于高速列车,整个车辆-轨道耦合系统振动的原因可能是车轮缺陷也可能是轨道不平顺。钢轨波浪形磨损是钢轨沿纵向表面出现的周期性的类似波浪形状的不平顺现象。Zarembski和 Grassie[2,3]按照波长确定机理和损伤机理对其进行了分类,指出低频力P2共振导致钢轨塑性弯曲、滚动接触疲劳和波谷纵向振动磨损,从而分别形成波长为500 mm~1 500 mm、150 mm~450 mm、150 mm~450 mm的波磨。
本文以谐波波磨激励模型进行计算,谐波激励模型如文献[1]。
单一谐波激励模型:

组合谐波激励模型:

公式中a为波的深度;L为波长;n为波数。
根据上述的波磨特点,本文的谐波激励模型假设为两种不同波长(波长分别为L1=300 mm、L2=1 500 mm)的钢轨面波浪形磨损叠加在轨道垂向谐波不平顺(波长L3=6 m)上,即激励为三种不同波长的谐波组合。
2.4 系统动力学特性的分析
为了研究车辆-轨道耦合系统动力学的时域特性,需要在时域上对由方程(5)~(9)组成的高阶微分方程组进行动力学计算。对于这种大型复杂非线性动力学高阶微分方程组,目前只能采用直接数值积分法,本文采用翟婉明[1]提出的新型快速显式积分求解此方程组。为了研究不同车速下特别是高速情况下,波浪形磨损和轨道不平顺对车辆的振动响应的影响,本文选取的速度分别为 350 km/h、300 km/h、250 km/h、200 km/h。通过计算得到了在激励模型下,系统的动力学响应特性如轮轨接触力、轮对加速度、转向架加速度、车体加速度等,典型的计算结果如轮轨垂向接触力如图2所示。

图2 不同速度下的轮轨力Fig.2 Vertical contact force at different speed
图2中,V-F表示轮轨垂向力,在轨面波浪型磨损与轨道垂向谐波不平顺的激励下,轮轨垂向力V-F呈现准周期波动(由于赫兹非线性接触力存在,轮轨力并不是绝对的周期变化),随着车速的提高,轮轨力不断增大。同时可见,轮轨力由这样几部分组成:①静态载荷;②波浪性磨损引起的动载荷;③轨道垂向不平顺引起的动载荷。计算和识别它们对轮轨力的贡献能了解不同波长波磨对轮轨接触力的影响。而前述的改进的EMD方法具有自适应的特性,能对复杂信号(轮轨力、加速度等)进行分解,系统各个部分的动力学指标均能通过这种方法进行分析。
3 车辆-轨道耦合动力学模型
3.1 轮轨接触力特性的提取与分析
在前述的激励模型下,轮轨垂向力及其分解如图3所示,V-F表示轮轨垂向力,V-F c1~c3表示其本征函数,V-F r3表示剩余分量,即静态轮轨力。车速为350km/h。改进的EMD方法将垂向轮轨接触力完全分解:V-F c1的幅值为28.25 kN;V-F c2的幅值为12.22 kN;V-F c3的幅值为4.96 kN,即高频力成分占到动态轮轨力的62%,中频轮轨力占到动态轮轨力的27%,低频轮轨力仅仅占动态轮轨力的1%。同理,计算得到速度为 300 km/h、250 km/h、200 km/h情况下动态轮轨力的成分组成:它们的高频成分分别占到动态轮轨力的50%、43%、46%;它们的中频成分分别占到动态轮轨力的39%、48%、43%。在四种不同车速下,波长分别为L1=300 mm、L2=1 500 mm的钢轨面波浪形磨损引起的轮轨力分别占到动态轮轨力的89%、89%、91%、88%,是动态轮轨力的主要成分。

图3 垂向轮轨力分解(350 km/h)Fig.3 Decomposition of vertical contact force
图4为不同车速下垂向轮轨力本征函数的比较结果。对于高频轮轨力成分V-F c1,车速越高,幅值越大,从350 km/h ~200 km/h,其数值分别为 28.25 kN、18.97 kN、13.64 kN、9.02 kN。对于中频轮轨力成分 V-F c2,其值不随车速线性变化,在车速350 km/h时,其幅值为12.22 kN;车速为300 km/h时,其幅值为14.93 kN;车速为 250 km/h 时,其幅值为 14.85 kN;车速为200 km/h时,其幅值为8.40 kN。对于低频力,其幅值随着速度降低而降低,从350 km/h~200 km/h,其数值分别为 4.96 kN、3.84 kN、2.59 kN、2.2 kN。

图4 垂向轮轨力本征函数(IMF)Fig.4 Intrinsic mode functions of vertical contact force
由此可见,波磨引起的轮轨力是动态轮轨力的主要成分,速度越高,高频动态轮轨力所占比例越大,中、低频轮轨力所占比例越小。
3.2 转向架动态特性的提取与分析
在前述的激励模型下,不同车速下转向架的垂向加速度响应本征函数的比较及其分解结果如图5所示。

图5 转向架加速度响应本征函数(IMF)Fig.5 Intrinsic mode functions of bogie acceleration response
Acc c1~c3为其加速度响应的本征函数,Acc r3为其剩余分量。对于其低频加速度响应成分Acc c3,车速越高,幅值越大,从200 km/h~350 km/h,其数值分别为0.46 m·s-2、0.67 m·s-2、0.85 m·s-2、1.04 m·s-2。中频加速度响应成分Acc c2随速度非线性变化,最大幅值为1.46 m·s-2,出现在250 km/h;其次幅值为1.31 m·s-2,出现在300 km/h;再次幅值为0.99 m·s-2,出现在350 km/h;最小的幅值为0.91 m·s-2,出现在200 km/h。高频加速度响应成分Acc c1也随速度非线性变化,最大幅值为0.53 m·s-2,出现在300 km/h;最小的幅值为0.39 m·s-2,出现在200 km/h。
由此可见,转向架加速度响应的低频与中频成分幅值大于高频成分,速度越高,低频加速度响应幅值越大,中、高频加速度响应呈非线性变化。
3.3 车体动态特性的提取与分析
在前述的激励模型下,不同车速下车体垂向加速度响应本征函数的比较结果及其分解如图6所示,Acc c1~c3为其加速度响应的本征函数,Acc r3为其剩余分量。高频加速度响应成分Acc c1随速度非线性变化,最大幅值为0.022 m·s-2,出现在250 km/h;其次幅值为0.019 m·s-2,出现在300 km/h;再次幅值为0.18 m·s-2,出现在 200km/h;最小的幅值为0.016 m·s-2,出现在350 km/h。对于其低频加速度响应成分也随速度非线性变化,当车速为250 km/h,其Acc c2与之对应且其幅值最大为0.026 m·s-2。其它车速时Acc c3与之对应:在车速为200 km/h,其幅值为0.015 5 m·s-2;在车速为 300 km/h,其幅值为0.014 6 m·s-2;在车速为 350 km/h,幅值为 0.015 m·s-2。

图6 车体加速度响应本征函数(IMF)Fig.6 Intrinsic mode functions of car body acceleration response
由此可见,由于一系悬挂和二系悬挂的隔离,车体的加速度响应及其分量随速度非线性变化,且其幅值变化的范围很小,小于乘车舒适度标准0.13 g,因此车体具有很好的舒适性。对于不同车体,也可以通过此方法研究其设计参数的合理性、乘坐舒适度。
4 结论
本文对经典的EMD方法进行了适当的改进:①以改进的极值域均值模式分解方法(IEMMD)提高局部均值的求解精度;② 以边界波形匹配预测法抑制端点效应。同时运用车辆-轨道耦合动力学,计算了系统在波浪形磨损和垂向谐波不平顺组合情况下的各种动力学响应(轮轨力、轮对和车体的加速度响应)。然后运用改进的EMD方法对系统的动力学响应进行了经验模式分解,详细分析了各个响应分量及其变化规律。计算结果表明这种改进的EMD分解方法自适应地将信号分解成本征模态,能有效地提取车辆-轨道系统的动力学特性。
[1]翟婉明.车辆轨道耦合动力学[M].北京:中国铁道出社,1997:20-60.
[2]Zarembski A M.Type of rail corrugation[J].Rail Gazette International.1989,85(8):12-13.
[3] Grassie S L ,Kalousek J.Rail corrugation:characteristics,cases and treatments[J].Proceeding of the Institution of Mechanical Engeersrs,1993,207:57-68.
[4]张继业,金学松,张卫华.高频力轮轨相互作用下钢轨的波磨[J].摩擦学学报,2003,23(2):128-131.
[5]张 洁,陈春俊,林建辉.基于小波变换的轨道不平顺信号分析[J].西南交通大学学报,2004,39(4):469-471.
[6]余 泊.自适应时频分析方法及其在故障诊断中的应用[D].大连:大连理工大学,1998.
[7]盖 强.局域波时频分析方法的理论研究与应用[D].大连:大连理工大学,2001.
[8] Zhao J P,et al.Mirror extending and circular spline function for empirical mode decomposition method[J].Journal of Zhejiang University,2001,2(3):247-252.
[9]邓拥军.EMD方法及Hilbert变换中便捷问题的处理[J].科学通报,2001,46(3):257-263.
[10]邵晨曦,王 剑,范金锋,等.一种自适应的EMD端点延拓方法[J].电子学报,2007,35(10):1944-1946.
[11]徐志胜,翟婉明,王开云.基于Timoshenko梁模型的车辆轨道耦合振动分析[J].西南交通大学学报,2003,38(1):22-27.
[12]雷晓燕,张 斌,刘庆杰.列车-轨道系统竖向动力分析的车辆轨道单元模型[J].振动与冲击,2010,29(3):168-173.
[13]宋 颖,杜彦良,孙宝臣.压电传感技术在轮轨力实时监测中的应用探讨[J].振动与冲击,2010,29(1):228-232.
[14] Gullers P,Andersson L,Lundén R.High-frequency wheel-rail contact forces-field measurements and influence of corrugation[C].Proceedings of the Seventh International Conference on Contact Mechanics and Wear of Rail/Wheel Systems,Brisbane,Australia,September 2-27,2008,265,1472-1478.

