三相PWM变换器传导干扰的预测分析
孙亚秀, 孙睿峰, 陈炳才
(1.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001;2.哈尔滨电业局,黑龙江哈尔滨 150001)
三相PWM变换器传导干扰的预测分析
孙亚秀1, 孙睿峰2, 陈炳才1
(1.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001;2.哈尔滨电业局,黑龙江哈尔滨 150001)
为了预测整流-逆变-感应电机系统的传导干扰,建立系统的共模和差模等效电路。等效电路由干扰源和耦合通道构成,用干扰源的数学模型代替电力电子器件开关时的非线性环节,对整流桥产生的共模和差模干扰采用傅里叶变换得出共模和差模干扰源的表达式,对逆变桥产生的共模和差模干扰采用双重傅里叶积分法得出干扰源的表达式,根据共模和差模传播路径的不同给出耦合通道相应的高频模型,根据整流桥和逆变桥各自产生的共、差模干扰源以及共、差模传播通道的高频模型构成的共模和差模等效电路,采用叠加原理得出整个系统的共模和差模干扰。仿真和实验结果验证了等效电路的正确性,建立干扰源和耦合通道频域模型的方法适用于整流-逆变-感应电机系统传导干扰的定量预测分析。
PWM驱动;傅里叶变换;双重傅里叶积分;耦合通道;共模等效电路;差模等效电路
0 引言
随着开关管开关频率的不断提高,脉宽调制(pulse width modulation,PWM)驱动的电机系统的传导干扰也日趋严重[1-3],众所周知,电磁干扰的形成必须具备三要素,即干扰源、耦合途径及接收器。为了能有效抑制PWM驱动的电机系统产生的传导干扰并使其达到国家电磁兼容标准,需要对PWM驱动电机系统进行预测分析。
电磁兼容预测主要是通过建立电路的等效模型来实现,准确有效的模型不仅能用来进行电磁干扰(electromagnetic interference,EMI)的预测,而且有利于滤波器的设计[4-8]。传导干扰最基本的预测模式是干扰源加干扰耦合通道[9]。对干扰源的建模主要有时域建模和频域建模两种方法,采用时域模型很容易理解系统的 EMI发射机理[10-11],精确的时域模型能够反映真实的干扰情况,对于简单的电路仿真时间也会很长,对于较复杂一些的电路,往往得不到仿真结果。采用频域模型能够快速地预测 EMI频谱,文献[12]从电路的角度介绍了变换器传导电磁干扰集中等效电路的频域建模方法,提出一种简单易行的方法估计变换器的噪声源和内阻抗,通过共模噪声源、共模内阻抗和差模噪声源、差模内阻抗来预测滤波器的抑制效果。文献[13]的建模思路与文献[12]相似,只是采用不同的方法得出等效电磁干扰源及其等效内阻抗,该文献提出一种测量变换器内部电磁干扰特性的新方法,定量地得出装置内等效电磁干扰源及其等效内阻抗。上述文献都是对简单的电路进行分析预测,对三相整流-逆变-电机系统的整体传导干扰预测的定量深入分析还未见报道。
基于此,本文以三相PWM驱动电机系统为例,分析传导干扰中共模和差模的产生机理,建立共模和差模干扰源的数学模型及干扰传播通道的电路模型,最后建立共模、差模干扰源及耦合通道的整体等效电路模型。通过仿真和实验来验证所建立的共模和差模整体等效电路模型的正确性和有效性。
1 干扰传播机理
本文的研究对象为三相变换器驱动的感应电机系统,其拓扑如图1所示,三相PWM驱动电机系统的电力电子器件工作在开关状态,具有较大的电压和电流变化率的功率脉冲信号产生很强的电磁干扰,但以传导干扰为主。根据干扰传播路径及产生机理的不同,传导干扰分为共模干扰和差模干扰。共模干扰主要是由脉动电压通过各相线对地寄生电容形成共模电流,再由地形成回路干扰。而差模干扰主要是相线之间的干扰直接通过相线与电源形成回路,主要由脉动电流引起。图1给出了本文所研究的电机系统的共模和差模的传输路径,文献[14]详细地介绍了图中的线路阻抗稳定网络(line impedance stablization net,LISN)。由图可见,在建立共模干扰流通路径时必须考虑整流桥和逆变桥的散热片对地的寄生电容以及电机对机壳的寄生电容,而建立差模干扰流通路径时必须考虑相线之间的寄生参数及直流测电容的寄生电感。
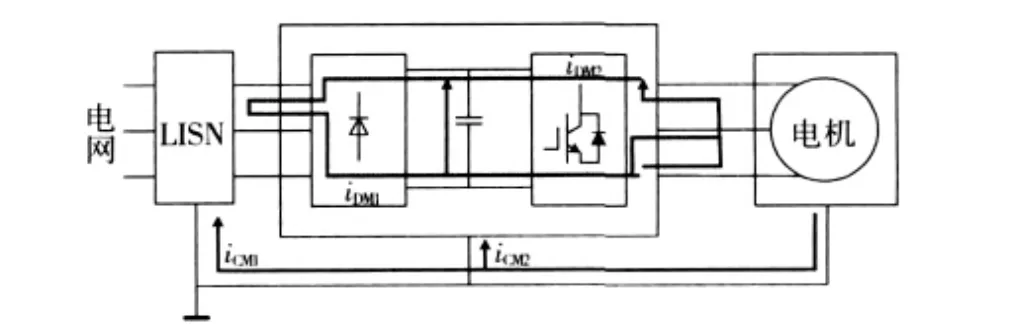
图1 三相变换器驱动的感应电机系统Fig.1 Induction motor system by three phase converter drive
2 干扰源的模型
2.1 整流桥产生的干扰源
图2为本节所研究的整流桥电路拓扑,图中给出了整流桥输出侧的共模和差模电流方向,其中Cp为系统对地的寄生电容,为共模电流提供通路。

图2 整流桥电路Fig.2 Circuit of commuting bridge

根据整流桥晶闸管不同时刻的开关导通情况得到u+和u-的傅里叶级数展开式为
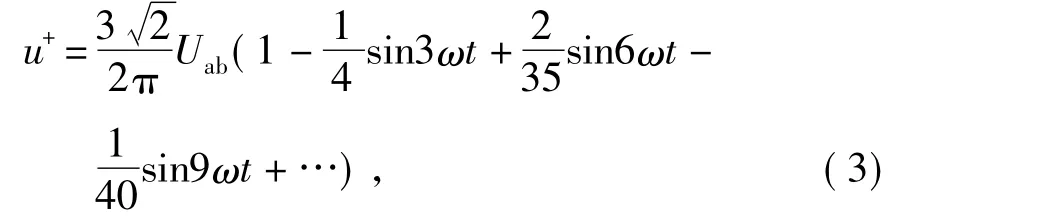
图3为整流桥侧接入LISN后的共模和差模等效电路图。整流桥输出侧的共模和差模电压的定义式为

式中:Uab为三相电源线电压,ω为电源角频率。
根据式(1)~式(4)得出整流桥侧共模和差模电压源的数学模型为
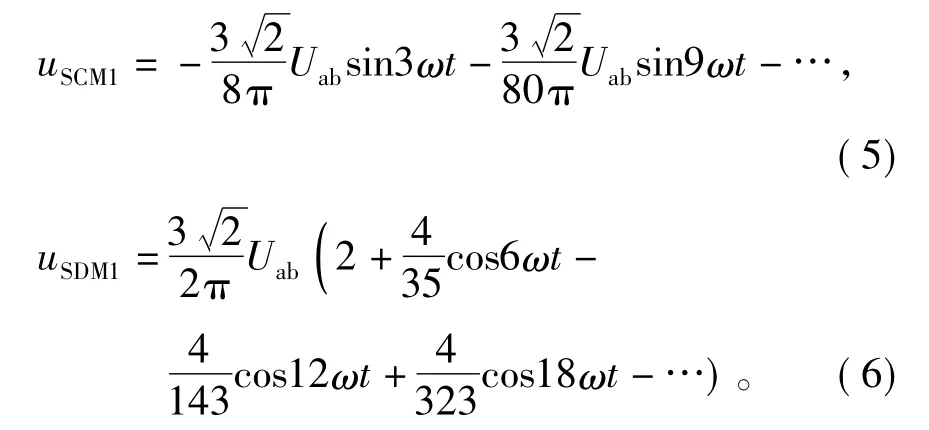
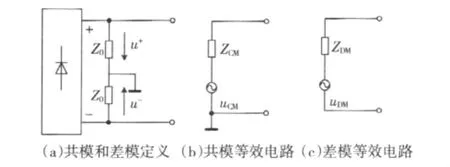
图3 整流桥接入LISN后的共模和差模等效电路图Fig.3 CM and DM equivalent circuit of commuting bridge connected to LISN
2.2 逆变桥产生的干扰源
图4为三相逆变桥拓扑,图中给出了逆变桥输出的共模和差模电流路径。在PWM逆变器中,共模电压定义为逆变桥输出中点对参考点的电位差,文中的参考点取为直流母线的中点O。输出的差模电压应为输出侧的线电压,详细的三相逆变桥侧的共模和差模电压的推导过程见文献[14],此处给出共模和差模电压的表达式为
逆变桥输出侧的共模和差模电压值随着功率管开关状态的变化而改变,此处的共模和差模电压的大小是由两个函数即载波和调制波共同作用得到的,要想将其作用后得到的共模和差模电压表示成数学模型,需用双重傅里叶积分法,将正弦脉宽调制(sine pule width modulation,SPWM)载波和调制波看成是双重傅里叶积分法中的两个函数,采样法采用对称规则采样法。所得到逆变桥输出侧的共模电压和差模电压的表达式为

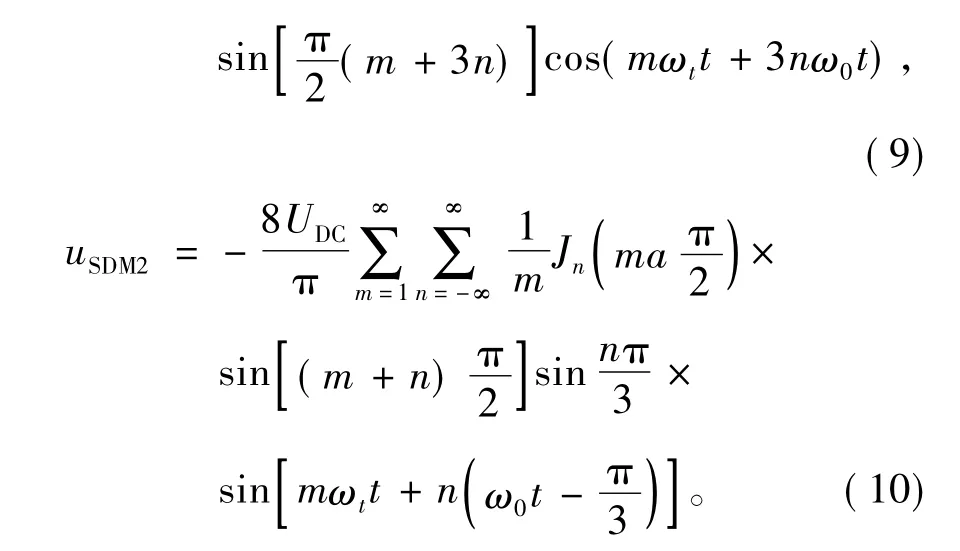
式中:a为调制比;ωt为调制波频率;ω0为载波频率;n表示调制波的第n次谐波;m表示载波的第m次谐波;Jn为n阶贝塞尔函数,其表达式为
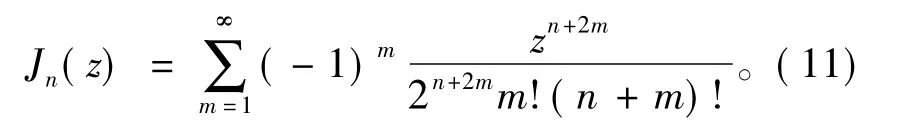

图4 三相逆变桥电路拓扑Fig.4 Circuit topology of three phase converter
3 传播通道的分布电路及参数确定
3.1 电缆的模型及参数确定
由于PWM驱动的功率变换器的电缆中所加的是高频脉冲信号,而且电缆的几何长度常常与所传输的信号波长在数量级上相当,所以不能忽略电缆本身固有的分布电感、电容等参数,需要采用传输线模型来描述电缆固有分布参数的传输特性,如图5所示。
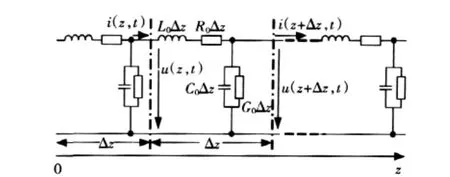
图5 平行传输线等效电路Fig.5 Equivalent circuit of parallel transmission line
图5中Δz为传输线的一个微小段几何长度,L0、R0、C0、G0分别为 Δz微段长传输线分布电路参数的集总表示,他们的大小由传输线的几何尺寸、相互空间位置及周围媒质的物理特性决定,而与电磁量无关,但却可以通过有关场量求出。对于常规电缆而言,虽然其特性参数是未知的,但是由于电缆等传输线模型的串联参数R和L与短路阻抗相关,并联参数C和G与开路阻抗特性相关,所以特性参数可以通过较宽频率范围内的短路阻抗Zsc和开路阻抗Zoc的实际测量值计算得到。
对于三相两电平PWM驱动电机系统,功率变换器工作的每一瞬间,电流总是从一根电缆流出,而从另外两根电缆流回,即两相并联后再与另一相串联。由于电缆线芯与屏蔽层之间绝缘介质的电导率为零,所以为简单起见,此处忽略电导G,于是,电缆的每根导线参数可以表示为

式中:flow为阻抗测量时的低频值;fhigh为阻抗测量时的高频值;Real[]为取实部函数;Image[]为取虚部函数。
由于实验所采用的PWM驱动电机系统的电缆长度不长,故采用传输线集总的π型等效电路,图6为四芯电缆的集总参数模型,电缆中的参数参照式(12)~式(14)来计算。

图6 电缆的集总参数模型Fig.6 Lumped parameter model of cable
3.2 电机的模型及参数确定
在进行传导干扰分析时,由于干扰信号属于高频信号,所以在建立感应电机模型时,必须考虑电机绕组和定子铁心的趋肤效应、线圈之间的容性耦合、绕组和定子铁心之间的容性耦合、铁心损耗和电磁场渗透性的降低等对电机阻抗产生的影响。由传输线理论可知,采用多导体、多单元传输线模型是研究感应电机绕组高频特性的最有效方法。对于给定的电机而言,每个定子槽的结构相同,槽内绕组匝数和线径均为定值,定子铁心为均匀且各向同性的线性媒质,所以可以认为感应电机绕组为均匀传输线。以一相绕组为例,本文采用更为简化的集总参数模型,选用π型电路为感应电机单相绕组模型的拓扑结构,如图7所示。
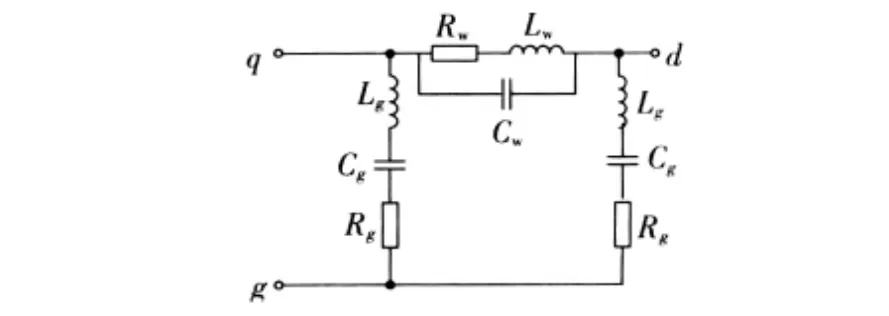
图7 感应电机单相绕组的高频电路模型Fig.7 High frequency circuit model of single phase induction motor
图7中,Rw为电机内部铁心涡流效应和线圈绕组的交流电阻;Lw为定子绕组的电感;Cw为定子绕组线圈的寄生电容;Rg为定子铁心叠片和机壳的总交流电阻;Lg为定子铁心电感;Cg为定子线圈绕组与地之间的寄生电容,包括定子线圈绕组与槽之间的寄生电容、定子铁心叠片之间的寄生电容、定子铁心叠片与电机机壳之间的寄生电容。
图7中的参数值根据阻抗Zqg和Zqd的转折频率以及他们的测量结果来确定。根据电路理论可以得到阻抗Zqg和Zqd的转折频率分别为

对于通常的感应电机而言,由于在传导干扰频段150 kHz~30 MHz内,其对地阻抗特性表现为容性,所以此时定子线圈绕组对地寄生电容Cg对Zqg的作用最大,并且在频率f=150 kHz处定子铁心叠片和机壳的交流阻抗Rg和铁心电感Lg对Zqg的作用最小,于是有下列近似关系存在,即

对于 Rg、Rw,由于转折角频率 ωz2(qg)、ωz2(qd)分别为阻抗Zqg和Zqd的谐振点,于是有

对于参数 Lg、Cg、Lw、Cw的值可以根据式(15)、式(16)、式(19)和式(21)以及阻抗Zqg和Zqd的实验结果来获得。
4 共模和差模等效电路
4.1 共模等效电路
前面已推导出整流桥和逆变桥的共模干扰源的数学表达式,因此可以用等效共模干扰源代替系统中的非线性环节,再根据共模干扰的传播途径利用电缆和电机的高频模型及对地的寄生参数建立共模等效电路。由于等效电路主要是由电阻、电感和电容等线性元件构成的,因此符合叠加原理,而傅里叶变换有线性性质,所以系统的共模干扰频谱就是不同共模干扰源作用下的频谱叠加。
由于共模干扰电流主要是流过各相线对地的寄生电容,再流过地形成回路干扰,所以在建立共模干扰流通路径时必须考虑整流桥和逆变桥的散热片对地的寄生电容以及电机对机壳的寄生电容,其中电机对机壳的寄生电容在电机绕组模型中已经表示出来,此处只须考虑整流桥和逆变桥的散热片对地的寄生电容即可,从而得到由整流桥共模干扰源和逆变桥共模干扰源共同作用时的系统的共模等效电路图,如图8所示。图中uSCM1和uSCM2分别为整流桥共模干扰源和逆变桥共模干扰源;Rc1、Lc1和 Cc1为电机电缆的参数;Rc2、Lc2和Cc2为电源电缆的参数;Rw、Lw、Cw、Rg、Lg、Cg为电机的参数;Cp为散热片对地的寄生电容,由阻抗分析仪测量得到。图中M点为直流母线中性点,LISN表示2个50 Ω的电阻并联。

图8 三相变换器驱动的感应电机系统的共模等效电路Fig.8 CM equivalent circuit of induction motor system by three phase converter drive
由图8可见,可以应用叠加原理分别计算出不同干扰源产生的共模电压,然后进行简单的叠加即可得到总的干扰。整流桥产生的共模干扰源单独作用时落到LISN上的共模电压为

考虑逆变桥产生的共模干扰源作用下的干扰分析,根据电路的叠加原理,逆变桥产生的共模干扰源uSCM2单独作用时,应将整流桥产生的共模干扰源uSCM1视为短路,由电路的基尔霍夫电压定律可得到由逆变桥共模干扰源单独作用时落在LISN上的共模电压为


上述公式中的单位均为V,将其转换为由电磁干扰测量标准规定的单位dBμV后可得

利用式(27)即可计算出能够与标准相比较的系统的总的传导干扰发射值。
4.2 差模等效电路
差模等效电路的建立方法与共模相似,根据差模干扰的流通路径,需考虑直流侧电容的寄生电感。而且由于整流侧的差模信号是通过两条电源线形成回路,而逆变桥侧的差模电流信号则是由一相流出而由两相流回,因此差模等效电路中由电缆模型形成的差模电缆阻抗与共模完全不同,而且在同一个差模等效电路中,由于整流侧和逆变侧的差模电流的流通路径不同,所以整流侧和逆变侧的差模电缆阻抗也会有所不同。
图9为整流桥产生的差模干扰源单独作用时的差模等效电路图,落到LISN上的差模电压为

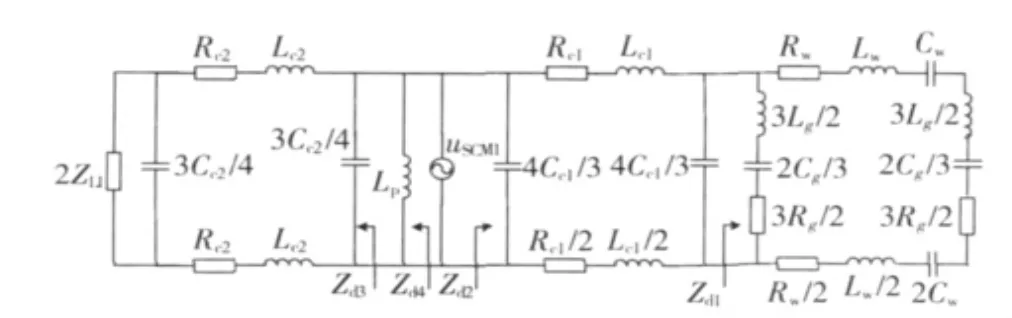
图9 整流桥差模干扰源单独作用时的差模等效电路Fig.9 DM equivalent circuit of system only effected by rectifier bridge DM source
将各参数带入式(28),即可计算出由整流桥差模干扰源产生的差模电压。
图10为逆变桥产生的差模干扰源单独作用时的差模等效电路,落到LISN上的差模电压为

根据基尔霍夫电压定律,即可计算出总的差模干扰电压为
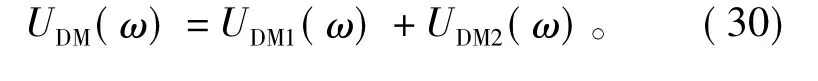
将上述公式转换为由电磁干扰测量标准规定的单位dBμv后可得


图10 逆变桥差模干扰源单独作用时的差模等效电路Fig.10 DM equivalent circuit of system only effected by converter DM source
5 实验研究
建立三相整流-逆变-电机系统,对其传导干扰进行了测试。系统参数为:智能功率模块(intelligent power module,IPM)型号为 PS21867(30 A/600 V);逆变桥开关频率为10 kHz;调制比a=0.8;电机型号为Y2-90S-4;整流桥型号为MDS30A/1 600 V。测试的设备为LISN和接收机ER55CR,接收机的测量带宽为9 kHz~30 MHz。对于上述实验系统,根据前面的高频模型参数的求取方法可得参数为:Rw=66 Ω;Lw=6.37μH;Cw=54.67pF;Rg=34.68Ω;Lg=4.83μH;Cg=154.68 pF;Rc1=Rc1=11 mΩ;Lc1=Lc2=15.7 μH;Cc1=Cc2=1 100 pF;Cp=16 nF。
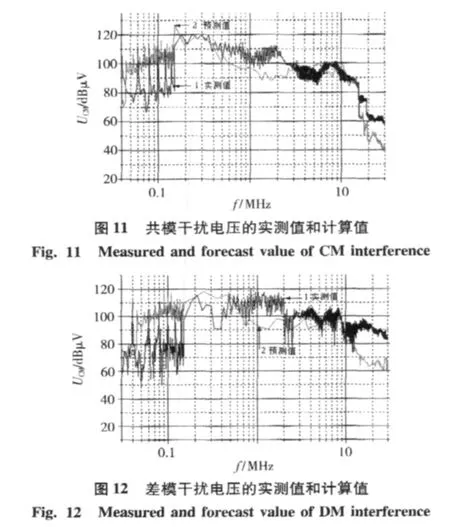
图11为系统产生的共模干扰电压的实际测量结果和计算结果,图中曲线1为通过LISN由接收机所测得的实际共模干扰电压,曲线2为通过等效电路计算所得到的共模干扰电压,是预测的结果。由图11可见,在低频情况下,预测的干扰电压比实测的干扰电压高,而在高频段实际测量值却比预测值大,这是因为预测模型中的耦合通道是按照系统最坏的工作情况来建立的,所以在低频情况下,预测的结果比实测的结果高。在高频段实际测量值比预测值大的主要原因是所建立的共模和差模的等效电路的耦合通道可能不完全准确,具体表现两个方面:一方面可能有没预料到的耦合通道,系统实际工作时干扰耦合途径可能会比理论上所分析的耦合通道多;另一方面所建立的耦合通道的高频寄生参数和实际的耦合通道的寄生参数也会有误差。由图11可见,预测值和实测值在整个频段上的频谱曲线的走势还是很接近的,这说明所建立的共模干扰源模型及共模等效电路有一定的参考价值。
图12为系统产生的差模干扰电压的实际测量结果和计算结果,图中曲线1为通过LISN由接收机所测得的实际差模干扰电压,曲线2为通过差模等效电路计算所得到的差模干扰电压,是预测的结果。从图中可以看出,在低频情况下,预测的差模干扰电压同样比实测的差模干扰电压高,而在高频段实际测量值却比预测值大,此情况和共模的预测情况相似,具体原因也和共模干扰情况相似。由图12可见,预测值和实测值在整个频段上的频谱曲线的走势还是很接近的,这说明所建立的差模干扰源模型及差模等效电路有一定的参考价值。
6 结语
本文对PWM驱动电机系统的共模和差模干扰进行了分析。首先建立干扰源的数学模型,用数学模型来代替系统的非线性环节,然后分析干扰的传播通道,建立传播通道及感应电机的高频模型,最后将干扰源和传播通道的高频模型联合起来建立高频的共模和差模等效电路来计算干扰。将计算得到的干扰频谱与实际测到的干扰频谱进行对比,对比结果表明,除高频段误差稍大外,其他频段实测值和计算值基本吻合,证明了该等效电路的有效性。此方法也可应用于其他的功率变换器系统,通过计算快速得到干扰的发射强度。
[1] REVOL B,ROUDET J,SCHANEN J L,et al.EMI study of a three phase inverter-fed motor drives[C]//Conference Record of the 2004 IEEE Industry Applications Conference,39th IAS Annual Meeting,October 3-7,2004,Seattle,USA.2004,4:2657-2664.
[2] BALCELLS J,SANTOLARIA A,ANTONIO O,et al.EMI reduction in switched power converters using frequency modulation techniques[J].IEEE Transactions on Electromagnetic Compatibility,2005,47(3):569-576.
[3] SKIBINSKI Gary,TALLAM Rangarajan,REESE Robert,et al.Common mode and differential mode analysis of three phase cables for PWM AC drives[C]//Conference Record of the 2006 IEEE Industry Applications Conference-Forty-First IAS Annual Meeting,October 8~12,2006,Tampa,USA.2006,2:880-888.
[4] AMARIR Said,AL - HADDAD Kamal.A modeling technique to analyze the impact of inverter supply voltage and cable length on industrial motor-drives[J].IEEE Transactions on Power Electronics,2008,23(2):753 -762.
[5] PEREZ A,SANCHEZ A M,REGUE J R,et al.Characterization of power-line filters and electronic equipment for prediction of conducted emissions[J].IEEE Transactions on Electromagnetic Compatibility,2008,50(3):577-585.
[6] GULEZ K,ADAM A A.High-frequency common-mode modeling of permanent magnet synchronous motors[J].IEEE Transactions on Electromagnetic Compatibility,2008,50(2):423 -426.
[7] KELLER C,FESER K.Fast emission measurement in time domain[J].IEEE Transactions on Electromagnetic Compatibility,2007,49(4):816-824.
[8] ZHAO Zhihua,YUAN Jiansheng,MA Weiming.Coupling model and impedance calculation of the steel ground loops with proximity effect[J].IEEE Transactions on Electromagnetic Compatibility,2006,48(3):522-529.
[9] 裴雪军,康勇,熊健,等.PWM逆变器共模传导电磁干扰的预测[J].中国电机工程学报,2004,24(8):83-88.PEI Xuejun,KANG Yong,XIONG Jian,et al.Prediction of common mode conducted EMI in PWM inverter[J].Proceedings of CSEE,2004,24(8):83-88.
[10] LI R,GOKANI S,CLARE J,et al.Conducted electromagnetic emissions in induction motor drive systems part I:time domain analysis and identification of dominant modes[J].IEEE Transactions on Power Electronics,1998,13(4):757 -767.
[11] LI R,GOKANI S,CLARE J,et al.Conducted electromagnetic emissions in induction motor drive systems partⅡ:frequency domain models[J].IEEE Transactions on Power Electronics,1998,13(6):768-776.
[12] 孟进,马伟明,张磊,等.变换器传导电磁干扰集中等效模型参数估计方法[J].电工技术学报,2005,20(6):25-29.
MENG Jin,MA Weiming,ZHANG Lei,et al.Parameter estimation of lumped circuit models for conducted EMI in power converters[J].Transactions of China Electro Technical Society,2005,20(6):25-29.
[13] 和军平,姜建国,陈斌.电力电子装置传导电磁干扰特性测量的新方法[J].电力电子技术,2001,35(5):32-35
HE Junping,JIANG Jianguo,CHEN Bin.A novel measurement of conducted EMI feature of power electronic equipment[J].Power Electronics,2001,35(5):32 -35.
[14] 孙亚秀.PWM驱动电机系统传导干扰问题的研究[D].哈尔滨:哈尔滨工业大学,2008.
(编辑:于双)
Forecast of conducted interference of three-phase PWM drive motor system
SUN Ya-xiu1, SUN Rui-feng2, CHEN Bing-cai1
(1.Information and Communication Engineering College,Harbin Engineering University,Harbin 150001,China;2.Heilongjiang Harbin Electric Power Bureau,Harbin 150001,China)
With the object of rectification-inversion motor system,Common mode equivalent circuit and differential mode equivalent circuit are founded to predict interference in this paper.Equivalent circuit is composed of interference source and coupling path.Nonlinear part of power electronic device is replaced by noise source math models.Noise source math models of rectifier and inverter should be calculated separately.For noise source from rectifier,the expressions about common mode and differential mode can be attained by applying Fourier transform.For noise source from inverter,double Fourier integral transform can be applied.Based on common mode and differential mode respectively,the corresponding high frequency models of coupling path were created.Based on superposition theory,common mode interference and differential mode interference of the whole system were educed by equivalent circuit.The simulation and experiment results demonstrate that equivalent circuits are valid.Quantity prediction analysis of conducted interference is realized first to rectification-inversion motor system.
pulse width modulation drive;Fourier transform;double Fourier integral;coupling path;common mode equivalent circuit;difference mode equivalent circuit
TM 921.5
A
1007-449X(2011)05-0042-07
2010-10-11
国家自然科学基金(60902014);中国博士后基金(20100480966);黑龙江省博士后基金(LBH-Z09215)
孙亚秀(1974—),女,博士,讲师,研究方向为电力电子系统电磁兼容、舰船电磁兼容;
孙睿峰(1972—),男,硕士,研究方向为配电网潮流计算;
陈炳才(1976—),男,博士,副教授,硕士生导师,研究方向为舰船电磁兼容。

