大型水轮发电机阻尼条数对电磁参数和附加损耗的影响

霍菲阳， 李伟力， 王冬梅

(1.北京交通大学电气工程学院，北京 100044;2.哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨 150080)

大型水轮发电机阻尼条数对电磁参数和附加损耗的影响

霍菲阳1， 李伟力2， 王冬梅2

(1.北京交通大学电气工程学院，北京 100044;2.哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨 150080)

针对大型水轮发电机稳态运行时阻尼条根数的变化对附加损耗的影响，以五强溪电站水轮发电机为例，结合发电机结构的对称性，给出相应的求解域和数学模型，利用有限元方法，计算水轮发电机在稳态运行时，极靴表面阻尼条分别为6根和8根2种结构下的电磁场。在此基础上，计算稳态运行时极靴表面2种结构的直、交轴同步电抗和直轴瞬态电抗，稳态运行时，阻尼条增加2根后对直轴和交轴同步电抗和直轴瞬态电抗影响均不明显。将计算结果与实验值进行比较，计算结果满足工程实际要求。此外，计算2种结构下空载和负载时的附加损耗，结果表明阻尼条根数增加，空载额定电压时极靴表面的附加损耗略增加，定子绕组高次谐波在极靴表面产生的附加损耗略小。

水轮发电机;电磁场;同步电抗;瞬态电抗;附加损耗

0 引言

大型水轮发电机中，阻尼条对于电机的稳定运行及抑制振荡具有重要的作用。正常运行时阻尼绕组并不感应出电流;当发电机转速忽高忽低变化时，阻尼绕组会产生反向阻尼转矩阻止转子转速的摆动;不对称运行时，阻尼绕组中可使负序旋转磁场产生的电磁转矩减小，电机的振动和噪音也相应地减小。因此，阻尼条根数的选择成为了研究电机动态运行时的重要内容［1－5］。此外不同阻尼条根数对交、直轴同步电抗稳态参数、电压调整率及电网并联运行时有功和无功功率的调节也会产生直接影响。而发电机稳态时的阻尼条数的变化使附加损耗也产生了一定的变化［6－10］。

本文以五强溪水轮发电机为例，运用有限元的方法，分别计算6根和8根阻尼条的结构下，电机的直轴、交轴饱和同步电抗和瞬态电抗，空载时极靴表面的附加损耗和负载时极靴表面及阻尼绕组中的附加损耗，与设计值和实测值比较，分析阻尼条根数对它们的影响。

1 稳态运行时饱和同步电抗的计算

1.1 基本假设

为简化分析，做如下假设［11－13］:

1)磁场沿电机轴向设为不变，因此可以简化为二维场来处理;

2)忽略电机端部磁场效应，磁场沿轴向均匀分布，即电流密度矢量J和磁位矢量A只有轴向分量;

3)不计曲率的影响，采用直角坐标系;

4)不考虑电机向铁心外部散磁，电机定转子铁心外缘矢量磁位均为零。

1.2 直轴同步电抗的计算

以五强溪水轮发电机为例，当阻尼条为6根时，建立电磁场的数学模型，其基本参数:额定功率为277.78 MW，额定电压为15 750 kV，额定电流为10 183 A，额定转速为68.2 r/min，极数为88，定子绕组Y型连接。

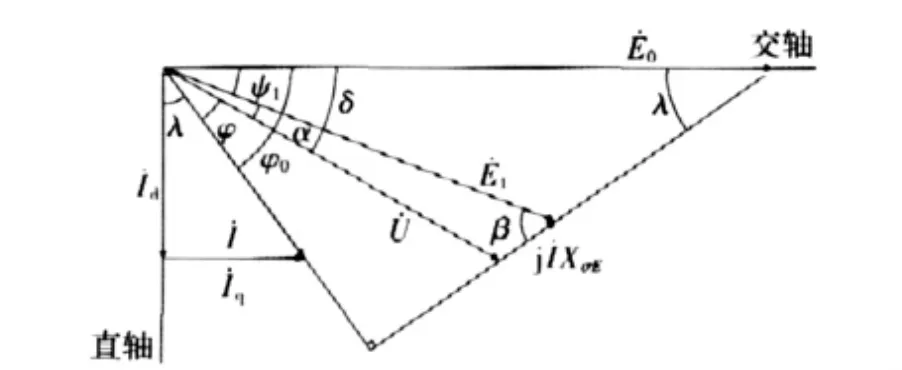
图1 水轮发电机的向量图Fig.1 Vector diagram of the hydro-generator

先预选一个额定励磁电流IfN和定子电流和与直轴间的夹角λ，λ=90°－φ0，如图1所示，由此可以确定定子槽内的三相电流的瞬时值［12］为

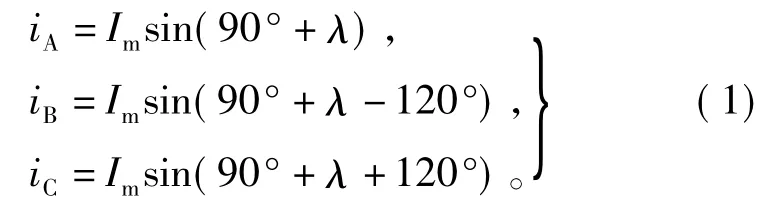
式中Im为定子电流的幅值。由于定子是分数槽绕组，取一个单元电机做为求解区域，如图2所示，在整个求解域内，矢量磁位满足边值问题为

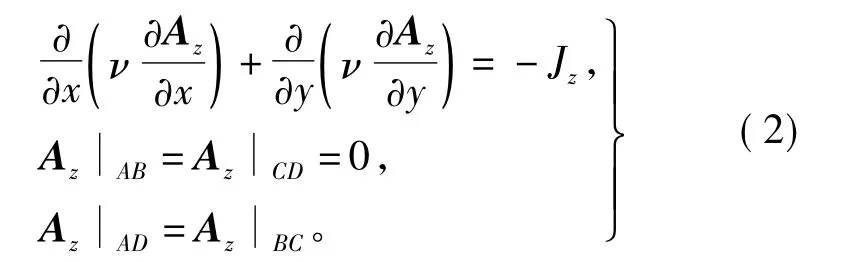
式中:ν为磁阻率;Az为磁量矢位，只有z轴分量。

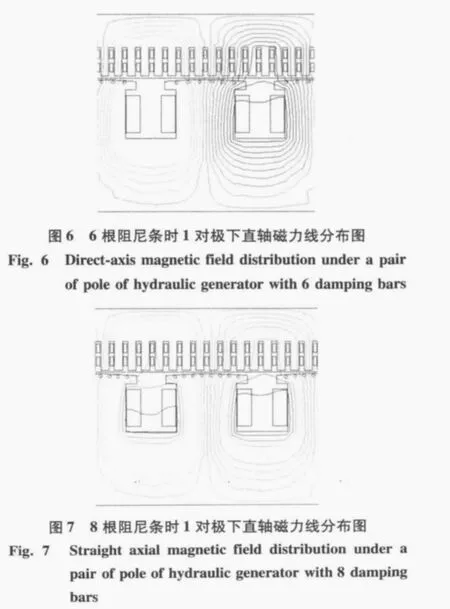
图2为五强溪水轮发电机6根阻尼条时直轴电磁场求解区域，对该求解区域进行离散剖分，其一对极下的局部放大剖分图如图3所示。将式(2)所对应的问题用牛顿－拉夫逊迭代法求解，使解答收敛。

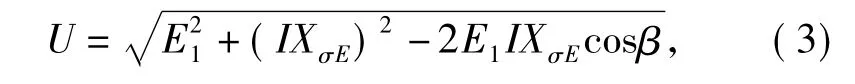
发电机端电压U为，如果不满足则应该调节励磁电流，可以调节转子励磁电流［14］为

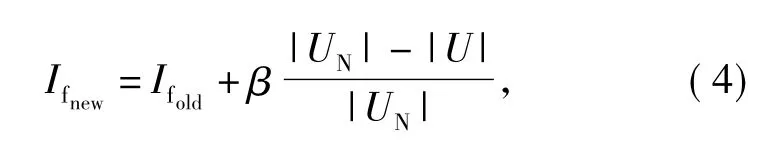
式中Ifnew、Ifold均为转子励磁电流的标幺值。

重复进行计算直到满足精确度为止。

经过端电压U和功率因数cosφ同时迭代满足精确度后，其气隙磁密谐波分解如图4所示，此时为6根阻尼条时的情况，8根阻尼条时其情况大体类似如图5。从图中可以看出，6根阻尼条时的谐波幅值略小于8根时的谐波幅值，因为增加了两根阻尼条，会在气隙磁场叠加谐波，使同等含量的谐波发生变化。

令定子A相绕组轴线和转子d轴之间的夹角θ=0°，由于定子为分数槽，则有

1.3 交轴同步电抗的计算

2 瞬态电抗的数值计算

2.1 基本假设

1)不计曲率的影响，采用直角坐标系;

2)励磁绕组端部的漏磁归并到直线部分，将三维问题简化为二维问题。

2.2 直轴瞬态电抗的计算

在定子加高频电流，电流幅值为Im=，转子静止，时，电机内的磁场为二维正弦电磁场，此时边值问题［12］为

在计算中，将物理模型由三维简化为二维，为保证计算精确，励磁绕组的端部漏磁可以归并到转子直线部分，即极身之间磁导率修改为原极身之间直线部分磁导率加端部漏磁，使二维和三维漏磁相等;极靴之间磁导率修改为原极靴直线部分磁导率加端部漏磁，也使二维和三维漏磁相等［12，14－15］，即

式中:μ0为原极身之间和极靴之间空间的磁导率;μ'和μ″分别为修改后的机身之间和极靴之间空间的磁导率;Λm为极身直线部分的漏磁导;Λme为极身端部的漏磁导;Λp为极靴直线部分和底面的漏磁导;Λpe为极靴端部的漏磁导，如图10所示，则有

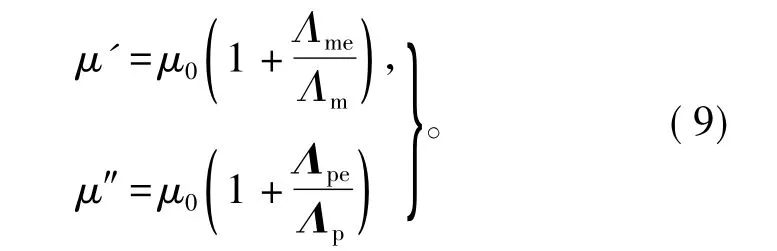
图10 励磁绕组端部漏磁的归并Fig.10 Conflation of magnetic leakage at the end winding

在转子静止，定子施加高频(s=108)、电流幅值为Im=的直轴脉振磁势，极身和极靴之间磁导率分别修改为 μ'和 μ″等条件下，求解式(5)，经多次迭代使z收敛，即可求出直轴瞬态电抗x'd，如图11所示;当阻尼条为8根时，情况类似如图12所示。

2.3 两种不同结构下计算出来的参数分别比较

由计算结果可以看出，其他条件不变，当阻尼条多加了2根后，对直轴、交轴的同步电抗和瞬态电抗变化并不是很明显，这是由于在稳态运行时，阻尼绕组上的涡流很小，对整个磁场的影响基本不大，所以对电抗参数影响不大，如表1所示;而8根阻尼条时各个参数均比6根阻尼条时略小，这是由于增加了2根阻尼条后，磁路的磁导变小，其他不变的时候，电抗必然变小，但阻尼条相对于整个电机占比例很小，使结果看起来并不明显。

3 空载和负载时附加损耗的计算

3.1 空载额定电压时极靴表面的附加损耗

水轮发电机中，极靴表面的附加损耗是由于电枢开槽，使得气隙主磁场上叠加了一个气隙磁导齿谐波磁场，电枢相对于磁极运动时，此齿谐波磁场就与磁极表面有相对运动，在磁极表面引起涡流损耗。

为研究齿谐波磁场在磁极表面引起的涡流损耗，假定:

1)谐波磁通密度在空间按正弦规律分布，其幅值为Bδ，忽略磁极表面涡流对Bδ削弱作用;

2)磁极材料的磁导率μ为常数;

3)磁极的轴向长度较长，磁极表面仅有轴向的电流。

根据电磁场方程［16］可得磁极单位表面积得涡流损耗PA为

将式(10)乘以所有磁极的表面积Aδ'即可得到电机的表面损耗，在以上电磁场计算的基础上，在水轮发电机空载的情况下，对求解区域计算，将式修改得到空载额定电压时极靴表面的附加损耗［16］为

式中:K1为系数，与磁极铁心冲片厚度有关;K2为修正系数;Kδ1为定子齿的气隙系数;Bδ为气隙平均磁通密度由电磁场计算后气隙磁密谐波分解得到。

3.2 短路电流为额定电流时定子磁场中齿谐波在

极靴表面及阻尼绕组中产生的附加损耗

由空载时极靴表面的附加损耗可以得到负载时定子磁场中齿谐波在极靴表面及阻尼绕组中产生的附加损耗［16］为

式中:K'为系数，当阻尼条为紫铜条时取2.5，当阻尼条为黄铜条时取10。

由式(12)即可算出短路电流为额定电流时定子磁场中齿谐波在极靴表面及阻尼绕组中产生的附加损耗。

表1 2种不同结构下参数比较Table1 Comparison of calculated parameters with two different structural

3.3 短路电流为额定电流时定子绕组磁势中高次谐波在极靴表面产生的附加损耗

由上述即可算出短路电流为额定电流时定子绕组磁势中高次谐波在极靴表面产生的附加损耗;根据以上方法，可以得到各附加损耗的值，如表2所示。

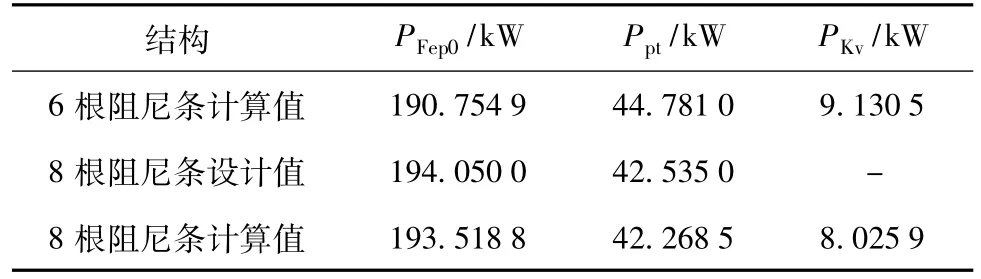
表2 两种阻尼条结构下计算出来的损耗比较Table 2 Comparison of calculated loss with two damping bars structural

由表2的计算结果可以看出，阻尼条增加2根后，由于阻尼条在定子也产生谐波，会对定子绕组磁势中的高次谐波起削弱作用，使定子高次谐波对极靴表面产生的损耗减小，但阻尼条增多后，其内部的损耗也随之增加，使极靴表面附加损耗随之升高，但变化都不明显。

4 结论

1)稳态运行时，对于25万千瓦水轮发电机，阻尼条增加2根后对直轴和交轴同步电抗影响约为5%，对直轴瞬态电抗影响约为0.6%，均不明显。

2)阻尼条根数增加，使空载额定电压时极靴表面的附加损耗略增加，对定子磁场中齿谐波在极靴表面及阻尼绕组中产生的附加损耗影响不明显，定子绕组中高次谐波在极靴表面产生的附加损耗略小。

3)用有限元方法计算出来的直轴和交轴同步电抗与实际测量时比较接近。

［1］ MINNICH S H，CHARI M V K，BERKERY J F.Operational inductances of turbine generators by the finite element method［J］.IEEE Transactions on Power Apparatus and System，1983，PAS102(1):20－27.

［2］ LANCAROTTE，M S，DE A PENTEADO A Jr.Estimation of core losses under sinusoidal or non-sinusoidal induction by analysis of magnetization rate［J］.IEEE Transactions on Energy Conversion，2001，16(2):174－179.

［3］ 黄进，许大中.阻尼绕组结构形式及结构参数对同步电机交－交变频调速系统特性的影响［J］.电工技术学报，1994，1(2):1 －5.HUANG Jin，XU Dazhong.Influences of damper structure and structural parameters on the performance of cyclo-converter fed synchronous motors［J］.Transactions of China Electrotechnical Society，1994，1(2):1－5.

［4］ FUNCHS E F，ERDELYI E A.Determination of waterwheel alternator steady-state reactances from flux plots［J］.IEEE Transactions on Power Apparatus and Systems，1972，PAS－91(6):2510－2527.

［5］ 汤蕴璆，梁艳萍.汽轮发电机的三阶模型和超－超瞬态电抗［J］.电工技术学报，2000，15(7):7 －11.

TANG Yunqiu，LIANG Yanping.The 3rd order model and subsubtransient reactance of turbogenerator［J］.Transactions of China Electrotechnical Society，2000，15(7):7－11.

［6］ 孙玉田.凸极同步电机的参数计算［J］.电机与控制学报，1997，1(2):75 －78.SUN Yutian.Parameter caleulation for salient pole synehronous maehines［J］.Electric Machines and Control，1997，1(2):75 －78.

［7］ JIANG Daiwei，YU Shenbo，AN Zhongliang，et al.Research on measurement of power angle and D-Q axis reactance parameters of REPM synchronous motor［C］//Sixth International Conference on Electrical Machines and Systems，November 9 －11，2003，Beijing，China.2003，1:76 －79.

［8］ 戈宝军，于涌源.3段圆弧极靴大型凸极同步电机稳态电抗计算［J］.电机与控制学报，1998，2(1):42 －46.GE Baojun，YU Yongyuan.Calculation of steady state reactances of large salient synchronous machine with three arc pole shoe［J］.Electric Machines and Control，1998，2(1):42 －46.

［9］ LANCAROTTE M S，PENTEADO A D，PAULOS A Jr.Prediction of magnetic losses under sinusoidal or nonsinusoidal induction by analysis of magnetization rate［J］.IEEE Transactions on Energy Conversion，2001，16(2):174－179.

［10］ 海勒尔B，哈马塔 V.异步电动机中的谐波磁场的作用［M］.张明涛，俞鑫昌，译.北京:机械工业出版社，1980:66－136.

［11］ 陈世坤.电机设计［M］.2版.北京:机械工业出版社，2000:44－73.

［12］ 汤蕴璆.电机内的电磁场［M］.2版.北京:科学出版社，1998:98 －173，369 －385.

［13］ 陈世元.交流电机磁场的有限元分析［M］.哈尔滨:哈尔滨工程大学出版社，1998:113－180.

［14］ DEMERDASH N A，HAMILTON H B，BROWN G W.Simulation for design purposes of magnetic fields in turbogenerators with symmetrical and asymmetrical rotors［J］.IEEE Transactions on Power Apparatus and Systems，1972，PAS －91(5):1985－1992.

［15］ 黄浩，梁艳萍.汽轮发电机励磁和参数数值计算［J］.防爆电机，2006，41(3):5 －8.

HUANG Hao，LIANG Yanping.Numerical calculation of exciting current and parameters of turbo-generator［J］.Explosion-proof E-lectric Machine，2006，41(3):5 －8.

［16］ 白延年.水轮发电机设计与计算［M］.北京:机械工业出版社，1982:522－580.

(编辑:张诗阁)

Influence of damper winding on electromagnetic parameters and additional loss of large hydo-generator

HUO Fei-yang1， LI Wei-li2， WANG Dong-mei2
(1.School of Electrical Engineering，Beijing Jiaotong University，Beijing 100044，China;2.College of Electrical and Electronic Engineering，Harbin University of Science and Technology，Harbin 150080，China)

Considering the effect of damping bars on additional losses，the hydraulic generator in Wuqiangxi power station was taken as an example.For the symmetrical structure of hydraulic generator，the solved region and mathematical model were given.Using the finite element method，the electromagnetic field of hydraulic generator with 6 and 8 damping bars were calculated separately while the large hydrogenerator was in steady-state operation condition.The direct-axis synchronous reactance，quadrature axis synchronous reactance and transient reactance of two different hydraulic generator structures were calculated.With increasing two damping bars，direct-axis synchronous reactance，quadrature axis synchronous reactance and transient reactance did not change significantly.Compared with the experimental values，the calculated results are in actual engineering requirements range.Besides that，the additional losses of the generator no-load and in load situation were calculated，and the additional losses increased with increasing the number of damping bar.The additional losses on boots surface of generator with 8 damping bars produced by stator winding higher harmonics are slightly smaller than the generator with 6 damping bars.

hydraulic generator;electromagnetic field;synchronous reactance;transient reactance;additional losses

TM 311

A

1007－449X(2011)05－0089－06

2009－11－02

国家重点科技支撑计划项目(2007BAA05B00)

霍菲阳(1979—)，女，博士研究生，研究方向为电机与电器多物理场计算;

李伟力(1962—)，男，教授，博士生导师，研究方向为大型电机综合物理场和特种电机理论;

王冬梅(1985—)，女，硕士，研究方向为大型电机综合物理场计算。