嵌岩扁桩承载力计算探讨

胡劲，冯暑，胡清，杨咏梅，胡先忠

（1重庆市市政委路桥收费处 重庆 400023 2重庆市瑞丰建筑勘察设计有限责任公司 重庆 402760 3重庆公用事业建设有限公司 重庆 401120）

嵌岩扁桩承载力计算探讨

胡劲1，冯暑2，胡清3，杨咏梅3，胡先忠2

（1重庆市市政委路桥收费处 重庆 400023 2重庆市瑞丰建筑勘察设计有限责任公司 重庆 402760 3重庆公用事业建设有限公司 重庆 401120）

嵌岩扁桩在房屋基础中较多见，由于现行桩基规范对其承载力的计算未明示，故扁桩承载力的准确计算有难度。本文通过对圆形嵌岩桩承载力的计算分析，提出扁桩桩径代表值的观点，并运用于扁桩承载力计算，较好地解决了扁桩承载力的计算问题。

嵌岩扁桩；桩径代表值；承载力计算；探讨

1 前言

近年来重庆地区的高层建筑日渐增多，对地基基础的承载力的要求也更高，为了满足上部建筑竖向作用力的要求，常采用大直径的人工挖孔扩底嵌岩桩，当两相邻挖孔扩底桩的最小中心距小于建筑桩基技术规范JGJ94-2008（以下简称“桩规”）表3.3.3规定，即1.5倍扩大端直径时，通常将两桩的扩大端相连组成连体扁桩或椭圆桩，一般组成连体扁桩的两桩扩大端的直径是相等的（也有不相等的情况）。对圆形嵌岩扩底桩，“桩规”给出了单桩竖向极限承载力的计算公式。如何运用圆桩的承载力计算公式来计算连体扁桩的竖向极限承载力，“桩规”中尚未明示，故实际操作起来有难度。笔者通过分析后提出扁桩桩径代表值的观点，从而可以运用圆桩的公式计算扁桩的承载力。

2 圆形嵌岩桩的竖向承载力

2.1 嵌岩桩单桩的竖向极限承载力

桩端置于完整、较完整基岩的嵌岩圆形截面单桩竖向极限承载力标准值Quk，由桩周土的总极限侧阻力标准值Qsk和嵌岩段的总极限阻力标准值Qrk两部分组成。Quk按“桩规”第5.3.9条的公式计算：

由式（2）可知，桩周土的总极限侧阻力与桩的周长、桩周土的极限侧阻力和桩长呈线性关系，与桩的嵌岩深度无关，因此用式（2）计算扁桩桩周土的总极限侧阻力是可行的。

由式（3）可知，桩嵌岩段的总极限阻力标准值与桩嵌岩段侧阻和端阻的综合系数ζr、岩石单轴抗压强度标准值frk和桩端截面积Ap呈线性关系。frk和Ap值是可以确定的，综合系数ζr值则是根据桩嵌岩段的深径比hr/d查“桩规”表5.3.9而得，扁桩的嵌岩深度hr是确定的，而扁桩的桩径有短直径、长直径、平均直径和换算直径等之分（其定义见3.1节），不同的直径就有不同的深径比，据此查表得的ζr值和计算的承载力就有差别，故必须首先确定扁桩桩径合理的代表值才能运用式（3）计算扁桩嵌岩段的承载力。

2.2 桩嵌岩段总极限阻力

“桩规”5.3.9条的条文说明给出了嵌岩段总极限阻力简化计算式，嵌岩段总极限阻力标准值Qrk由总极限侧阻力标准值Qrs和总极限端阻力标准值Qrp组成：

系数ζs和ζp可由“桩规”的表9查得。 但查系数ζs和ζp时需要计算嵌岩段的深径比，故必须首先确定扁桩桩径合理的代表值后才能用式（4）计算扁桩的承载力。

2.3 嵌岩扁桩竖向承载力计算现状

目前在嵌岩扁桩的竖向承载力设计中，通常将扁桩或椭圆桩的短直径或长直径作为扁桩或椭圆桩桩径的代表直径，据此计算扁桩的深径比，查表得综合系数ζr，代入“桩规”嵌岩圆桩的公式计算扁桩的竖向承载力Nik。在各种嵌岩深度下（岩石的单轴抗压强度标准值frk相同），分别用扁桩的短直径d1和长直径d4计算扁桩的竖向承载力N1k、N4k，然后计算这两组承载力的相对偏差。其计算结果列于表1、图1中。

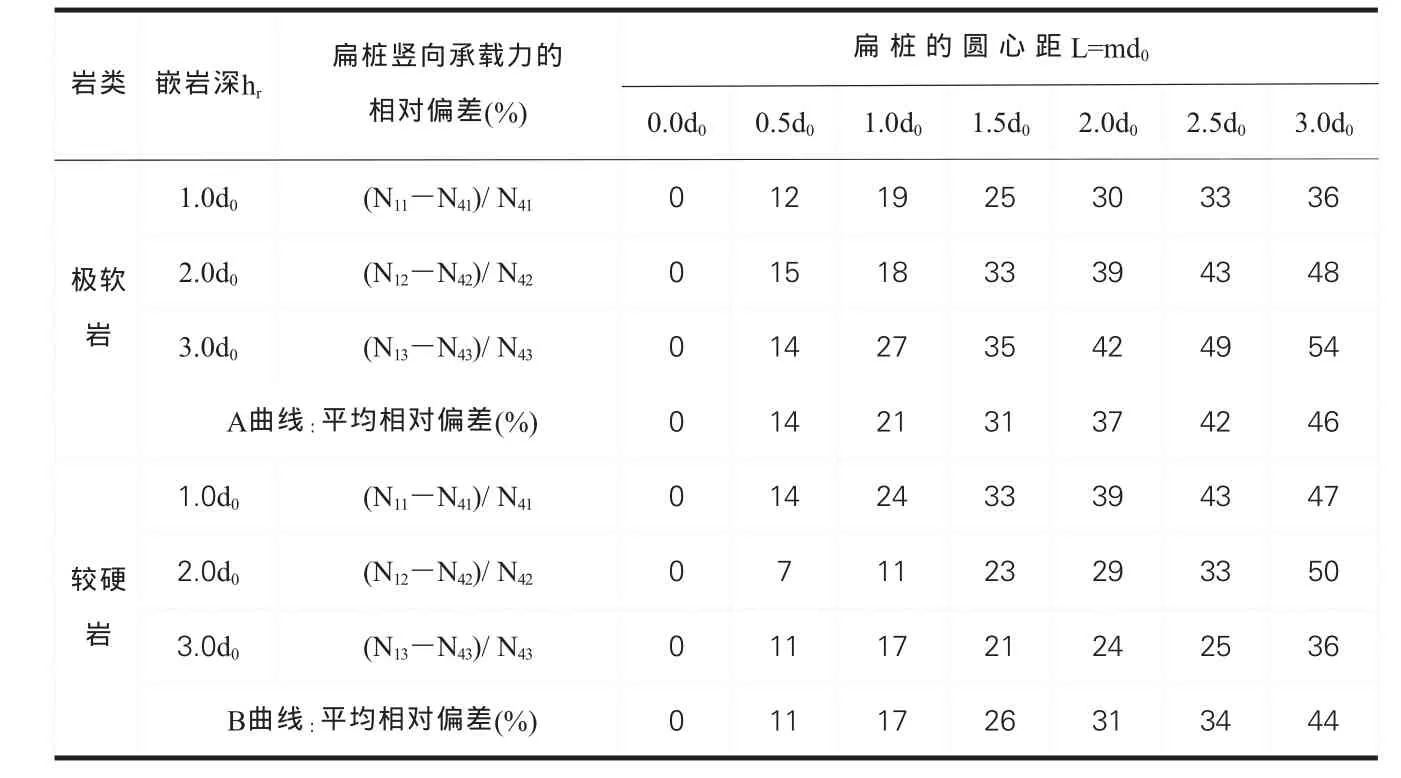
表1 在特定条件下扁桩的竖向承载力Nik的相对偏差值(%)表

图1 扁桩的A、B曲线图(L单位：d0)

分析表1和图1可得：A曲线较B曲线的偏差大，用短直径d1（扁桩平面的最小尺寸即圆桩直径）计算得的承载力N1k最大（偏高），用长直径d4（扁桩平面的最大尺寸）计算得的承载力N4k最小（偏低），两者的差值随圆心距L的增加而增加。当L=0～1.5d0时，A曲线的相对偏差率为0～31%，B曲线的相对偏差率为0～26%；当L=15～3.0d0时，A曲线的相对偏差率为31～46%，B曲线的相对偏差率为26～44%，显然这样大的偏差工程上是难以容许的，这样可能造成工程的浪费和安全隐患。扁桩的准确承载力值应该是介于两者之间，但如何取舍是有待商榷的。

综上所述，运用圆桩的公式来计算扁桩的承载力时，必须首先确定扁桩桩径合理的代表值，使承载力的计算误差尽可能小，既满足上部结构对承载力的要求，又避免造成工程的浪费和安全隐患。

3 嵌岩扁桩的竖向承载力

3.1 扁桩桩径的代表值

扁桩的横、竖剖面图见图2和图3。

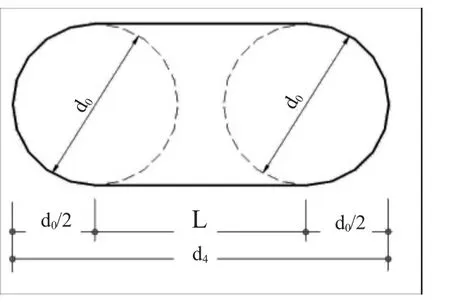
图2 扁桩的横剖面图

由图2、图3可知扁桩的嵌岩深度hr是确定的也是唯一的。扁桩的横剖面近似椭圆形，椭圆形的扁桩如何确定桩径合理的代表值，是较关键的问题。为比较，设组成扁桩的两个等直径圆桩的直径为d0，两圆桩的圆心距设为L，令L=md0，为此扁桩计算直径可选取以下4种计算方法：

（1）短直径d1=d0=（d01+d02）/2：组成扁桩的两个等直径圆桩的直径 （两圆桩的直径不相等时，可用两圆桩的平均直径代之）；

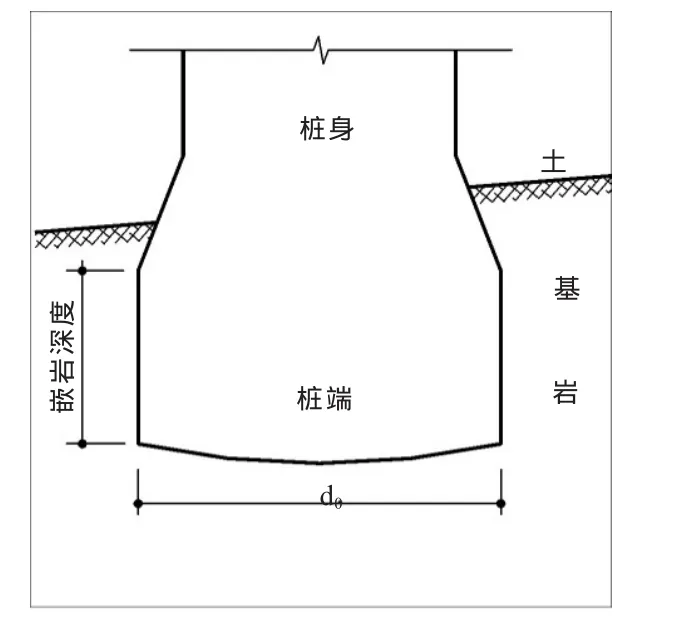
图3 桩的竖剖面图

扁桩的计算直径值di与圆心距L的关系见表2和图4所示。

表2 扁桩计算直径与圆心距的关系表

图4 di与L的关系图（di、L单位：d0）

由表2和图4可得：

（1）当L=0时，d1、d2、d3和d4的值均等于d0，即扁桩变为圆桩；

这里引入扁桩直径代表值的观点，用它代入圆桩的承载力计算式就可以计算扁桩的承载力。究竟用哪一个di作为扁桩直径的代表值计算承载力最恰当，下面将作分析。

3.2 扁桩承载力的计算图表

前已阐述，用圆桩的承载计算公式计算扁桩承载力的主要问题是桩径的代表值的确定问题。由于承载力与综合系数ζr成正比，研究综合系数的变化规律就能反映承载力的变化规律，故下面只讨论综合系数的变化规律。

现用扁桩的4种计算直径计算扁桩的深径比，由此查表得桩嵌岩段侧阻和端阻综合系数。扁桩嵌岩深度、计算桩径、圆心距与桩嵌岩段侧阻和端阻综合系数的关系见表3、表4和图5、图6。

表3 扁桩嵌岩深度、计算直径、圆心距与桩嵌岩段侧阻和端阻综合系数的关系表(极软岩、软岩干作业挖孔桩)

注：dik、ζik脚标i表桩直径的类别和对应的综合系数，k表嵌岩深度。

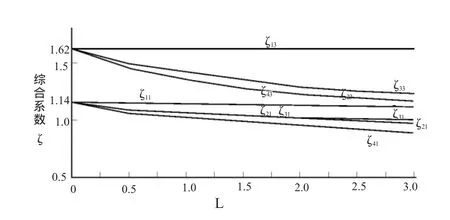
图5 hr=1d0、2d0时，ζik与 dii、L的关系图（极软岩、软岩，L单位：d0）

图6 hr=1d0、2d0时，ζik与dii、L的关系图（较硬岩、坚硬岩，L单位：d0）

表4 扁桩嵌岩深度、计算直径、圆心距与桩嵌岩段侧阻和端阻综合系数的关系表(较硬岩、坚硬岩干作业挖孔桩)

3.3 扁桩承载力计算分析

由表3、表4和图5、图6可得：

（1）当0.0d0≤L ≤3.0d0，嵌岩深度为零时：综合系数ζr均相等且与L的大小无关，此时的桩就是端承桩，竖向承载力可直接用端承桩的公式进行计算，毋须确定扁桩桩径的代表值；嵌岩深度hr相同时，短直径d1k对应的ζr值为常数，即为水平直线。

（2）当0.0d0≤L ≤1.5d0，嵌岩深度hr相同时：由平均直径d2和换算直径d3所查表得的综合系数ζr值随L的增加而减少，且基本相等，相互偏差率在1%以内，与L=0时相比ζr值的降幅为8.3～25.9%；当嵌岩深一定时，与d2和d3所对应的ζr值比与d1对应的ζr值小3～21%，比与d4对应的ζr值大3～10%，即d2和d3对应的ζr值曲线与d4对应的ζr值曲线较接近些，而与d1对应的ζr值曲线偏离较远些。

（3）当1.5d0＜L ＜3.0d0时：d2与d3所对应的ζr值偏差增大，相互偏差率在5.3%以内；ζr值随L的增加而降低的速率加快，与L=0时相比ζr值的降幅为17.5～35.2%。

故由上比较可知，当0.0d0≤L≤1.5d0时，扁桩的承载力：用平均直径d2和换算直径d3所得值较接近于用长直径d4所得值，偏离较小，与用短直径d1所得值偏离较大。故笔者认为用扁桩的平均直径或换算直径作为扁桩桩径的代表值来计算其承载力是稳妥的。

4 结语

通过上述分析，扁桩的承载力按“桩规”5.3.9式计算：用扁桩的短直径所得之值偏大，用扁桩的长直径所得之值偏小，用扁桩的平均直径或换算直径所得之值适中并偏于安全。扁桩的承载力计算在现行规范未明示前，笔者建议一般建筑可用平均直径或换算直径作为嵌岩扁桩桩径的代表值，并据此计算扁桩的承载力。对于重要或特殊的以及高地震烈度地区的建筑，为安全计建议用长直径作为嵌岩扁桩桩径的代表值为妥。

嵌岩深度为零时，毋须计算扁桩桩径的代表值，其竖向承载力直接按端承桩的公式进行计算。

建议今后加大对嵌岩扁桩的试验研究，探索扁桩和等效圆桩的受力作用机理的异同及关系，为扁桩的设计提供科学的依据。

[1]JGJ94-2008,建筑桩基技术规范[S].

[2]DBJ50-047-2006,建筑地基基础设计规范[S].

Bearing Capacities Calculation on Rock-Socketed Pickets

Rock-socket piles are commonly used in the house infrastructures.Its bearing capacity is difficult to be calculated accurately since it is not showed in the standard of the pile foundation rightnow.Byway of calculation and analysisof bearing capacity of the round rock-socketed pile,thisarticle puts forward the view of representative valueof thepilediameterand applies it to the calculation,solving the problem to a satisfactory degree.

rock-socketed pile;representative valueof thepile diameter;calculation of bearing capacity;discussion

TU 473.1+2

A

1671-9107（2011）07-0037-04

10.3969/j.issn.1671-9107.2011.07.037

2011-04-11

胡劲（1970-），大学本科，工程师，主要从事建筑设施建设和管理工作。

余咏梅