工业机器人视觉测量的优化校准

刘 丹

（湖南商务职业技术学院，长沙 410205）

0 引言

在先进自动化生产过程中，工业机器人视觉测量系统对关键尺寸进行在线实时监测，及时调整动作幅度和角度，可有效控制产品质量的稳定性[1,2]。由于结合了非接触测量方式和机器人运动灵活的优点，可以解决传统三坐标测量机对盲孔、深孔等的测量难题，也可以克服接触式测量头对复杂工件的干涉，在先进制造业中得到了逐渐推广和应用。实际的工业现场环境复杂，多种因素都有可能导致系统在运行过程中产生一定的偏差、测量精度降低，引起误差的原因主要有温度漂移和关节松动变形等，使测量模型的参数值改变从而导致定位误差增大，因此需要定期对工业机器人视觉测量系统进行精确的校准，从而实现精确定位和视觉测量。目前，国内外关于该领域的研究还比较少，也没有解决好工业机器人视觉测量的精确校准难题。本文对工业机器人的视觉测量误差模型进行了相关研究，建立了针对显著变化参数的测量误差模型，采用遗传算法去求解最优的模型参数，从而达到精确校准，可以满足工业机器人实际生产的要求。

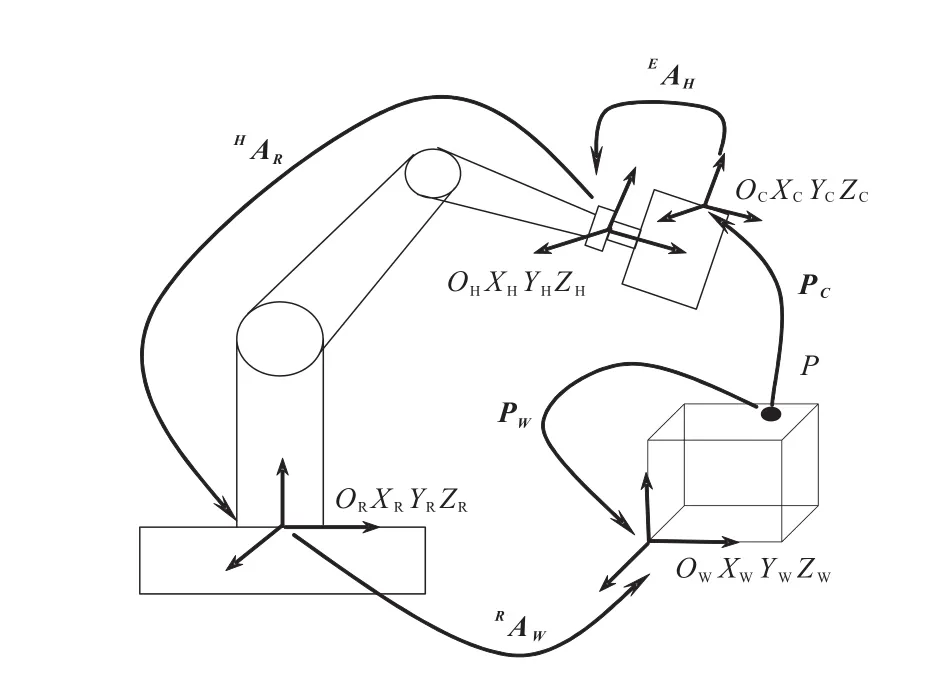
图1 测量系统工作原理

1 工业机器人测量系统工作原理

图1为应用于工业机器人的测量系统工作原理示意图。图中共存在4个坐标系，分别为机器人基础坐标系ORXRYRZR、机器人末端关节坐标系OHXHYHZH、工件坐标系OWXWYWZW和视觉传感器坐标系OCXCYCZC。

式（1）中，PC为被测点P在视觉传感器测量坐标系下的坐标值；为机器人手眼关系，即机器人末端关节坐标系到视觉传感器测量坐标系的齐次坐标变换关系，一旦传感器安装到末端关节上就保持不变；为机器人基础坐标系到装置坐标系的齐次坐标变换关系，工位安装完成后同样为定值；为机器人末端关节坐标系到机器人基础坐标系的齐次坐标变换关系，即

2 机器人视觉定位误差模型

采用D-H模型[3]对机器人进行分析，假设每个关节都存在连杆参数偏差，那么传感器坐标系相对于机器人基础坐标系的变换为

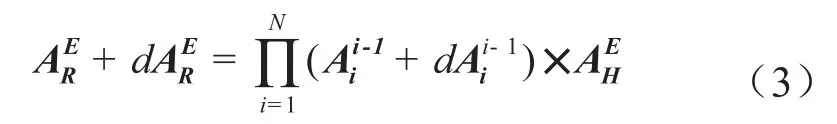
结合变换微分可以推导出末端关节相对于机器人基础坐标系的位置偏差为

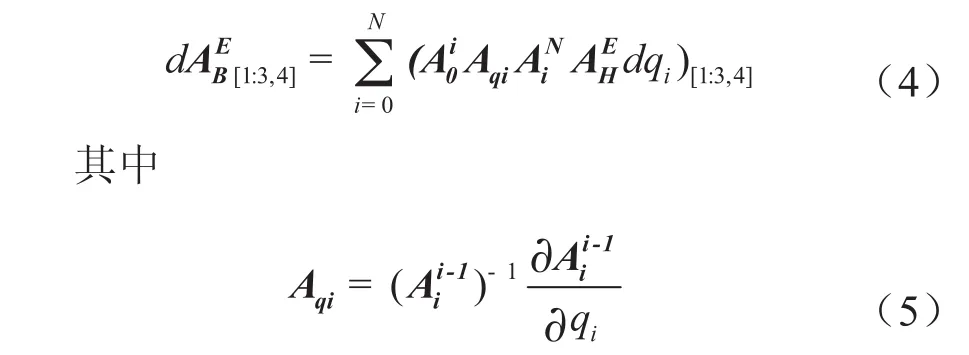
表示第 i个关节的连杆参数 qi、ai、ai、di，下角标[1:3,4]表示取对应矩阵第4列的1至3行。

为了说明本文的校准方法，这里以ABB2400型机器人为例，是一种典型的6关节工业机器人。

关节1单独转动时对机器人6个不同姿态的TCP进行了测量，关节2和关节3单独转动时各测量了5个不同姿态下的TCP坐标值，关节4、关节5和关节6单独转动时分别测量了9个、6个和10个不同姿态下的TCP坐标值。关节单独转动时，以关节2、关节3和关节4产生的偏差最明显，然而，当关节2和关节3同时转动时，TCP在y方向的定位偏差反而减小，这说明关节2和关节3同时转动会对y轴方向的误差有抵消作用。

结合大量的实验数据进一步分析，当关节1转动时，7个姿态中只有x方向的坐标出现了较大偏差，若考虑测量噪声的存在，其它方向的坐标值可以认为没有变化，对照机器人运动学模型，可以确定此时杆件长度参数a1产生了较为明显的变化。结合实际测量样本值，并以此类推，可以采用同样的方法总结出有可能产生较大变化量的模型参数如表1所示，分别描述了与各个关节关系较大的模型参数，这也是引起测量误差的主要因素和原因。只要我们能够确定出表1中的有关模型参数的准确值，就可以较好地实现工业机器人视觉测量的校准。

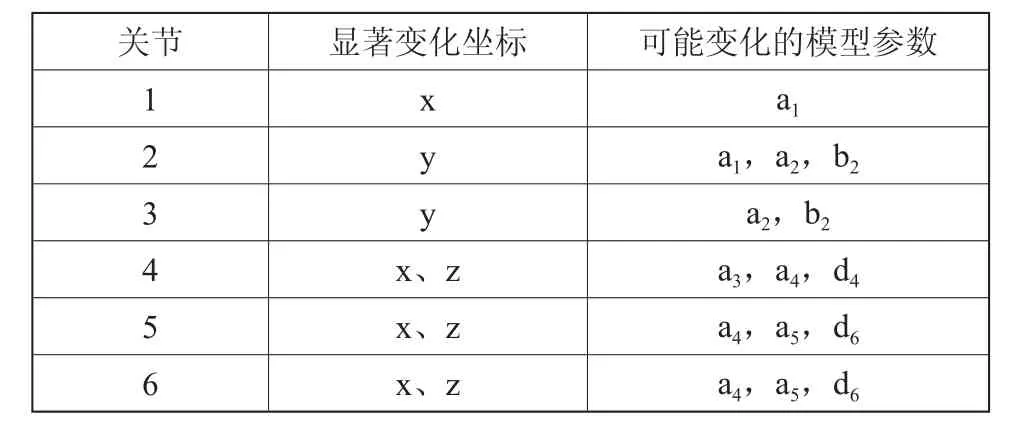
表1 机器人视觉测量误差模型

3 基于遗传算法的精确校准方法

由表1的分析可知，对于6关节的ABB2400型机器人，当发生温度漂移或者关节松动变形时，引起视觉定位中的某一些参数值发生变化，因而为了实现精确校准，就需要根据实际样本数据来寻找到最佳的参数值。根据上述分析可知，对于视觉测量校准而言，主要是对表1的模型参数予以寻优，当参数优化后，就可以克服温度漂移和关节松动变形等的影响，从而提高视觉测量准确度。这里采用遗传算法对这些参数予以优化，优化后得到的参数值将具有很好的测量准确度。

遗传算法（Genetic Algorithm）[4,5]是一类借鉴生物界的进化规律（适者生存，优胜劣汰遗传机制）演化而来的随机化搜索方法。它是由美国的J.Holland教授1975年首先提出，其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域[4,5]。

遗传算法主要有遗传、交叉、变异等几个模拟生物进化的过程组成，遗传算法的框架可非形式地表示如下：

Genetic_algorithm ()

{

t=1；／*变量t表示迭代代数*／

初始化候选群体Population (t)；

计算各个解的适应值；

do while (终止条件不满足)

{

随机地将种群中的个体两两配对，进行交配操作；

执行变异操作；

利用选择机制形成下一代候选解：

Population (t+I) =Selection (Population (t))；

t=t+ 1：

}}

遗传算法主要的特点体现在智能性和本质并行性两个方面．遗传算法智能性是由于在确定了编码方案、适应值函数及遗传算子后，利用演化过程中获得的信息自行组织搜索，因此具有根据环境的变化自动发现环境的特性和规律的能力；而其并行性是由它全局搜索方式决定的。按照遗传算法的程序，根据实际测量的样本数据值就可以计算得到最佳的模型参数值，以此得到确切的视觉测量值，避免温度漂移和关节松动变形等对测量结果准确度的影响。

4 仿真研究

这里我们选取了100组实际测量样本数据为依据来建立精确的视觉测量校准值，其中遗传算法的参数值为种群数为30，二进制码长度为20，交叉概率为0.45，变异概率为0.1。当采用遗传算法优化后，就可以根据新寻优的参数值作为视觉测量校准的精确值，从而得到比较准备的视觉测量结果。

仿真实验中，针对各个关节松动变形和温度漂移的情况，予以了实验验证，仿真结果如表2所示，描述了校准前和校准后的误差情况。表2的仿真结果表明，相比于校准前的误差值，根据本文方法校准后，视觉测量的准确度大大提高了，视觉测量的误差显著减小了，从而验证了本文算法的有效性。

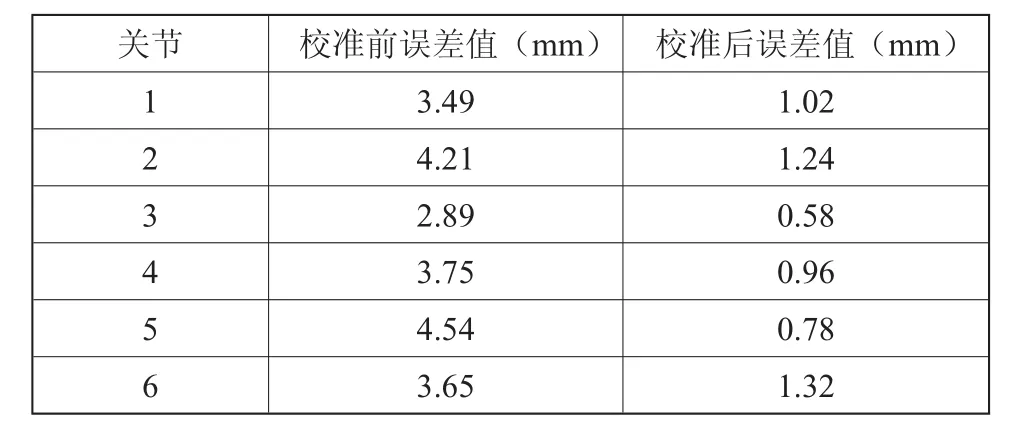
表2 视觉测量校准仿真结果

5 结束语

针对工业机器人视觉测量系统，本文提出了一种基于遗传算法的优化校准方法，首先根据机器人的D-H正向运动学模型和微分运动学模型建立末端关节坐标系的定位误差模型，然后利用遗传算法选择最优的参数值，从而实现了精确校准。仿真实验表明，该方法能大大减小视觉测量误差，可以满足实际生产的要求。

[1] 王一, 刘常杰, 任永杰, 等. 通用机器人视觉检测系统得全局校准技术[J]. 光学精密工程, 2009, 17(12): 3028-3033.

[2] 任永杰, 邾继贵, 杨学友, 等. 机器人柔性视觉检测系统现场标定技术[J]. 机器人, 2009, 31(1): 82-87.

[3] Denavit J, Hartenberg R S. A kinematic notation for lowerpair mechanisms based on matrices[J]. Journal of Applied Mechanics, 1955, 22(2): 215-221.

[4] 吉根林. 遗传算法研究综述[J].计算机应用与软件, 2004,21(2): 69-73.

[5] 李敏强. 遗传算法的基本理论与应用[M]. 科学出版社,2002.