基于遗传算法与蚁群算法的电网规划

唐杰斌，周渝慧，陈向婷，郭昱霄，段 炜

（北京交通大学 电气工程学院，北京 100044）

电网规划是电力规划的重要环节，如何加强主网网架结构是电网规划最重要的内容之一，也是规划成败的关键［1］。近年来，智能优化算法在解决多目标电网规划中得到了较广泛的应用，如：遗传算法、蚁群算法等。为了克服遗传算法与蚁群算法本身的缺陷，许多文献对其进行了改进：文献［2］提出了用竞赛法进行生殖操作、两点交叉、保留优良品种等改进措施；文献［3］提出了把改进的自适应代沟遗传算法引入电网规划分析网架优化；文献［4］通过改进传统的初始种群生成方法以及遗传操作使之更适应于电网规划；文献［5］提出一种基于Pareto蚁群算法的多目标电网规划方法，把多目标问题转化为单目标问题来进行电网规划。

在处理具体问题时，每种智能方法在优化性能与时间性能方面都表现出各自的优势与缺陷，各种改进算法旨在克服算法各自的缺陷，在增强算法本身优势方面做的工作并不多［6］。融合算法考虑到在处理电网规划问题上遗传算法的快速随机的全局搜索能力和蚁群算法的分布式并行全局搜索能力的优势，旨在将2种数学优化算法融合，从而弥补各自的缺陷，达到优势互补的目的。

1 电网规划问题的数学模型

为了验证融合算法在求解电网规划目标函数时相对单一算法的优势，本模型以新建的线路作为规划变量，以新建线路的投资年费用最小为目标函数，如式（1）所示［4］。

式中：i=1，2，…，n；j=1，2，…，n，i≠j，n 为系统节点数；cij为节点i、j之间架设一回新建线路的投资费用；t为节点i、j之间待选线数，在不同节点的待选线路中，t是不同的；xij的值表示节点i、j之间需架设待选线路数。

约束条件为：①流通性约束：确保每个负荷点均有网络连通；②潮流约束：实际传输的潮流应该不大于线路允许的最大潮流；③“N-1”校验约束：网络中任意一个区域在所有与之相连的线路中任何一条线路故障的情况下，其它线路的传输容量之和必须大于该区域的净负荷需求。

2 基于融合算法的电网规划

遗传算法和蚁群算法相融合，旨在弥补单一算法的缺陷，充分发挥2种算法各自的优势。由于遗传算法在求解到一定程度时会产生大量的冗余迭代，此时若改用蚁群算法则能有效避免冗余迭代，使求解的方案更加精确。同时，蚁群算法的初期信息素匮乏、求解速度缓慢，若在初期先用遗传算法产生最优解，生成蚁群算法初期的信息素，可以有效弥补蚁群算法初期信息素匮乏的缺陷［7］。图1为融合算法应用于电网规划的流程图。

图1 融合算法应用于电网规划流程图

2.1 染色体编码

生成蚁群算法初始化信息素的过程为遗传算法求解最优解的阶段，因此必须对求解的目标问题进行染色体编码。考虑到此染色体结果需要转化成蚁群算法的初始信息素，本文将待选的线路排序，每一条排好序的待选线路作为染色体的一个基因。基因采用十进制编码，即待选的走廊数均作为一个基因位，基因的数值大小则表示走廊架设的回路数，这样编码为转化成初始信息素提供方便，而且各走廊架设的线路数与基因位也一一对应［8］。其表达式如式（2）所示。

式中：x为目标函数的染色体编码；n为待选线路的数量；xi为输电线路走廊架设的线路回数；t为走廊待选回路数的最大值。

2.2 适应度函数

遗传算法将求解问题表示为染色体位串空间，为了执行适者生存的原则，必须对个体位串的适应性进行评价。本文以架设线路的费用最小为目标函数，因此将目标函数f与适应度函数g做相应的调整［6］，如式（3）所示。

在求解适应度函数时，将约束条件应用惩罚因子加以处理，当染色体满足目标函数的约束条件时，直接将目标函数代入式（3）计算染色体的适应值；当染色体不满足约束条件的限制时，则引入相应的惩罚因子。

2.3 遗传操作

遗传操作是保留优良个体、淘汰缺陷个体、保持种群多样性的重要操作，包括选择、交叉、变异。为了更好地保留种群中的优良个体，在选择前先对所有个体根据适应度排序，选择一定比例的个体直接遗传到下一代，然后对其他的个体利用基于转盘赌的选择方式进行选择操作。对于选定的2个个体位串，随机选择多个交叉点，构成交叉点集合，采用多点交叉方式进行交叉操作。变异是为了保持物种的多样性，但是变异的概率不能太大，否则容易变成随机算法，因而对不同的算例采用不同的变异概率，随机选择变异的个体，然后随机选择变异的基因，从而维持个体的多样性［9］。

电网规划编码采用实值形式，因此变异也采用实值变异，如式（4）所示。

2.4 蚂蚁转移概率

首先将m只蚂蚁放入n只随机选择的节点上，每只蚂蚁都以当前点为中心，按照伪随机比例规则选择并走到下一节点。蚂蚁每走一步后，都要对其走过的路径进行局部信息素更新，这样可避免所有蚂蚁收敛到同一路径。当m只蚂蚁中有一只到达目标点时，这只蚂蚁即为本次迭代的精英蚂蚁，对其所找到的路径进行全局信息素更新，使得属于本次迭代最优路径上的信息素得到增强，反之则会逐渐减弱［10，11］。

在蚂蚁转移过程中，蚂蚁会继续产生信息素，路线上原有的信息素强度也会随着时间的推移而挥发，当蚂蚁走完n个节点后，信息素浓度［6］

式中：ρ表示信息素的保留率，1-ρ表示信息素的挥发率，为了防止信息的无限累积，ρ取值范围限定在0～1；Δτij（t+n）表示蚂蚁k在时间段t到（t+n）的过程中，在i到j的路径上留下的残留信息浓度，本文采用的是ant-quantity 模型，如式（6）所示。

式中：Q为常数，对不同的算例取不同的值。

2.5 基于融合算法的电网规划

融合算法的基本思想就是在最佳衔接点采用遗传算法生成初始信息素分布，在最佳点之后采用蚁群算法求取最优解。遗传算法设置最大迭代次数Genmax、最小迭代次数Genmin，同时在迭代中引入子代最小进化率rmin，即子代平均适应度与父代平均适应度之差与子代平均适应度的比值。在迭代次数超过Genmin、小于Genmax的过程中，计算子代的进化率，若连续2代的进化率都低于最小进化率rmin，则输出遗传算法结果；若未超过则进入最大迭代次数。

遗传算法结束后，将计算结果以信息素的方式反映到各条规划线路上，即为蚁群算法初始信息素强度的一部分。另一部分为蚁群算法根据求解问题的具体规模给定的信息素常数，此2部分即为蚁群算法的初始信息素。随后，信息素更新模型利用式（5）进行信息素强度更新。由于遗传算法得出的最优解在一定程度上向最优方案接近，因此通过最优解转换成蚁群算法的初始信息素也加快了蚂蚁收敛的速度［12］。

融合算法求解电网规划的另一个问题是蚂蚁在寻找最优路径时［13］，通过转移概率选择某一输电走廊时还会涉及到选择的输电回路数，这是与蚁群算法求解旅行商问题（traveling salesman problem，TSP）的区别。因此，转移的概率公式也发生变化，它采用伪随机比例规则［14］选择下一路径，即设定一个常数q0，并生成一个在［0，1］上均匀分布的随机变量q，如果q≤q0，选择公式（7），否则选择公式（8）［15］。

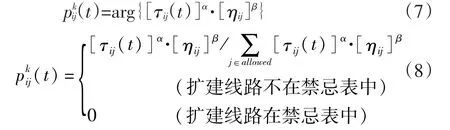
式中：α为轨迹的相对重要性；β为能见度的相对重要性；ηij为启发信息，本文主要考虑输电线路的扩建费用，取ηij=1/dij。

3 算例分析

算例采用文献［1］中的现有网络和待选路径，如图2所示。该系统现有10个节点，9条线路，未来系统将增加为18个节点，节点参数如表1所示。本算例存在新增的线路走廊21个，即取染色体长度为21位，待选线路33条，取染色体域N=100，交叉率pc=0.5，即交叉个数Nc=50个，变异率为0.5%，变异个数Nm=21，迭代次数为100次，线路单位长度造价3.0×105元/（km·回），蚂蚁个数为20，Q=100，α=1，β=5，ρ=0.7，最小迭代次数Genmin为40次，最大迭代次数Genmax为100次，本例中由于适应度函数由最小费用转化而来，因此最小进化率rmin=5%。

图2 网络路径示意图

表1 节点参数

若仅运用遗传算法求解，设置最大迭代次数为100，不同迭代次数的规划结果如表2所示。迭代次数为50次时，子代进化率约为3%，因此最佳迭代点为迭代50次的结果。同时，本算例也计算了迭代到100次的结果，绝对差别仅为0.123亿元，从扩建支路长度来看，扩建费用差别较少。因此可以认为在50次到100次迭代期间，产生了大量的冗余迭代。

若仅运用蚁群算法求解，设置迭代次数为150，不同迭代次数的规划结果如表3所示。迭代次数约为100次时，扩建费用与遗传算法迭代到50次时绝对差为0.093亿元，相对扩建线路长度来说，扩建费用差别较少。因此，可以认为在100次迭代之前产生的信息素与遗传算法迭代到50次产生的信息素相匹配。

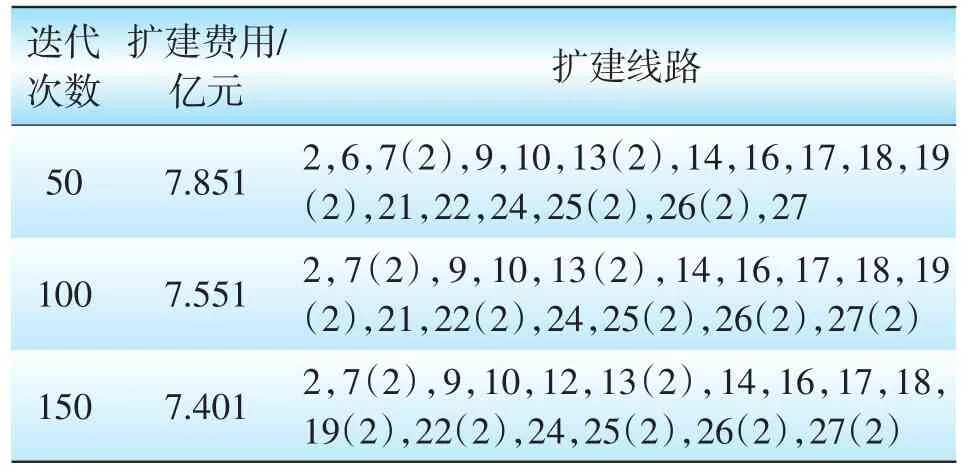
表3 蚁群算法规划结果

为了发挥遗传算法与蚁群算法各自的优势，采用融合算法，将遗传算法的迭代次数设置为50，蚁群算法迭代次数设置为100，其规划结果如表4所示。融合算法在迭代次数为50次时是遗传算法迭代50次的结果，迭代100次与150次时则是用遗传算法的最优解产生的初始信息素，再利用蚁群算法求解得到的最优方案，其最优方案的结果如图3所示［16］。

表4 融合算法规划结果

比较表2与表4迭代100次的结果可以发现，融合算法扩建费用比遗传算法高0.06亿元，这是由于融合算法是以遗传算法的最优解为初始信息素进行迭代，在使用蚁群算法迭代初期有一个适应过程，方能转化为最适合蚁群算法的解集，因此在迭代100次时出现这种结果是可能的。比较表3与表4可以发现，融合算法在迭代100次和150次时均有较大的改进。

图3 融合算法确定的网络结构

4 结论

使用遗传算法进行电网规划在迭代后期容易产生大量冗余迭代，大大降低了遗传算法求解电网规划的效率。蚁群算法处理电网规划问题时初始信息匮乏，最初求解速度缓慢。为了更好地运用遗传算法与蚁群算法的优势，引入融合算法进行电网规划，既能避免求解到一定程度后产生大量冗余迭代，同时也充分利用了蚁群算法求解精度高的优势，最终使得规划方案达到最优。

［1］ 王锡凡.电力系统规划基础［M］.北京：水利电力出版社，1994.

［2］ 张俊芳，王秀丽，王锡凡.遗传算法在电网规划应用中的改进［J］.电网技术，1997，21（4）：25-32.

［3］ 黄武忠，钟丹虹，孔德键，等.改进的遗传算法在汕头电网规划中的应用［J］.广东电力，2001，14（5）：8-11.

［4］ 顾益磊，许诺，王西田.遗传算法应用于电网规划的难点与改进［J］.电网技术，2007，31（增刊1）：29-33.

［5］ Miranda V，Ranito JV.Genetic algorithms in optimalmul-tistage distribution network planning［J］.IEEE Transac-tionson Power Systems，1994，9（4）：1927-1933.

［6］ 朱福喜，朱三元，伍春香.人工智能基础教程［M］.北京：清华大学出版社，2006.

［7］ 杨剑峰.基于遗传算法和蚂蚁算法求解函数优化问题［J］.浙江大学学报，2007，41（3）：427-430.

［8］ Gallego R A，Monticelli A，Romero R.Transmission sys-tem expansion planning by extended genetic algorithm［J］.IEE Proceedings Generation Transmission and Distribu-tion，1998，145（3）：329-335.

［9］ 林娇燕.运用改进遗传算法的输电网规划［J］.华南理工大学学报：自然科学版，2002，30（8）：36-39.

［10］ 符杨，孟令合，胡荣，等.改进多目标蚁群算法在电网规划中的应用［J］.电网技术，2009，33（18）：57-62.

［11］ Ippolito M G，Sanseverino ER，Vuinovich F.Multiobjec-tive ant colony search algorithm for optimal electrical distribution system strategical planning［C］.Portland：CEC 2004Congresson Evolutionary Computation，2004.

［12］ 韩富春，王晋，杨翠茹，等.遗传算法与蚂蚁算法相融合的电力系统最优潮流计算［J］.电力学报，2005，20（4）：340-342.

［13］ MarcoDorigo，Gambardella，Luca Maria.Ant colonies for the traveling salesman problem［J］.Biosystems，1997，43（2）：73-81.

［14］ 符杨，孟令合，朱兰，等.Pareto蚁群算法在多目标电网规划中的应用［J］.电力系统及其自动化学报，2009，21（4）：41-45.

［15］ 涂亚平，刘萍，谢宝陵，等.基本蚂蚁算法中算法参数的优化［J］.小型微型计算机系统，2007，28（11）：1985-1987.

［16］ 雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005.