配网分布式电源并网对电网潮流的影响
陈永秋,罗振威,顾 全
(1.江门供电局,广东 江门 529000;2.南京南瑞继保电气有限公司,南京 211100)
分布式发电(distributed generation,DG)通常是指发电功率在几千瓦至数百兆瓦的小型模块化、分散式、布置在用户附近的、高效、可靠的发电单元,主要包括:以液体或气体为燃料的内燃机、微型燃气轮机、太阳能发电(光伏电池、光热发电)、风力发电和生物质能发电等[1]。
分布式发电的优势在于可以充分开发利用各种可用的分散存在的能源(包括本地方便获取的化石类燃料和可再生能源),并提高能源的利用效率。分布式电源通常接入中压或低压配电系统,并会对配电系统产生广泛而深远的影响。
1 分布式电源潮流计算分析
传统配电网中一般包含2种节点类型:Vθ节点和PQ节点,其中:V为电压幅值;θ为相角;P为有功功率;Q为无功功率。变电站出口母线通常视为Vθ节点,其它节点(包括负荷节点和中间节点)都视为PQ节点。随着各种分布式电源加入配电网络,系统中出现了新的节点类型,主要包括:①P恒定、V恒定的PV节点;②P恒定、电流幅值I恒定的PI节点;③P恒定、V不定、Q受P和V限定的PQ(V)节点。在进行计算时,需要针对不同的节点类型采用不同的处理方法,其本质是在潮流计算的每个迭代步骤上将各种类型的节点转换成为传统方法能够处理的PQ节点或 PV 节点[2,3]。
由于牛顿法具有二阶收敛特性,在配电网潮流计算中仍然保持着收敛速度和迭代次数方面的优势。虽然配电网末端母线电压偏低,但正常运行情况下,各节点的电压也在额定电压附近,各节点的电压相角差也不会很大,初值采用平启动的方式,牛顿法都能得到满意的结果。所以在配电网潮流计算的实际应用中,牛顿法仍然是一种性能优良的潮流计算方法[4,5]。具体潮流计算流程如图1所示。
2 DG接入电网的性能评估
本文以IEEE-33节点母线测试系统为例,33节点配电系统如图2所示(0为平衡节点),支路编号与该支路的受端节点编号一致。三相功率的基准值SB=10MVA,线电压的基准值UB=12.66 kV,根节点电压标幺值为1.0,计算精度ε=10-6。系统总有功负荷为3 715 kW,总无功负荷为2 300 kvar。
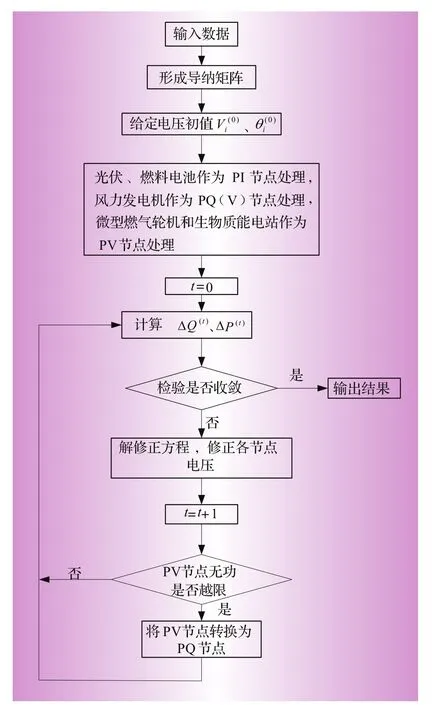
图1 含DG的配电网牛顿法潮流计算原理
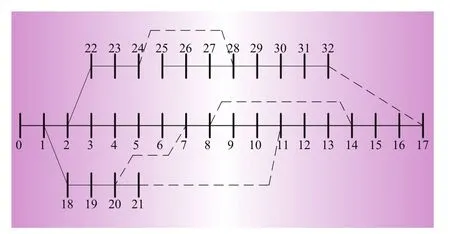
图2 IEEE-33母线测试系统
33节点配电系统中接入的各种类型的DG参数如下:①光伏电站:有功功率150 kW,I*=0.016 6;②燃料电池电站:有功功率250 kW,I*=0.027 7;③风力发电机:有功功率1.5 MW,定子电抗Xs=0.036 92Ω,定子电阻Rs=0.001 692Ω,转子电抗Xr=0.037 59Ω,转子电阻Rr=0.002 423Ω,励磁电抗Xm=1.456 8Ω,恒定功率因数0.89(滞后);④微型燃气轮机电站:有功功率150 kW,V*=0.98;⑤生物质能电站:有功功率2.5MW,V*=0.98。
2.1 光伏电站接入电网分析
以光伏电站接入电网后的潮流分析为例。假设在节点32处接入一台光伏电站,新节点编号为33,按照上述潮流计算方法分析,潮流计算结果如表1所示(迭代4次),节点电压曲线如图3所示。
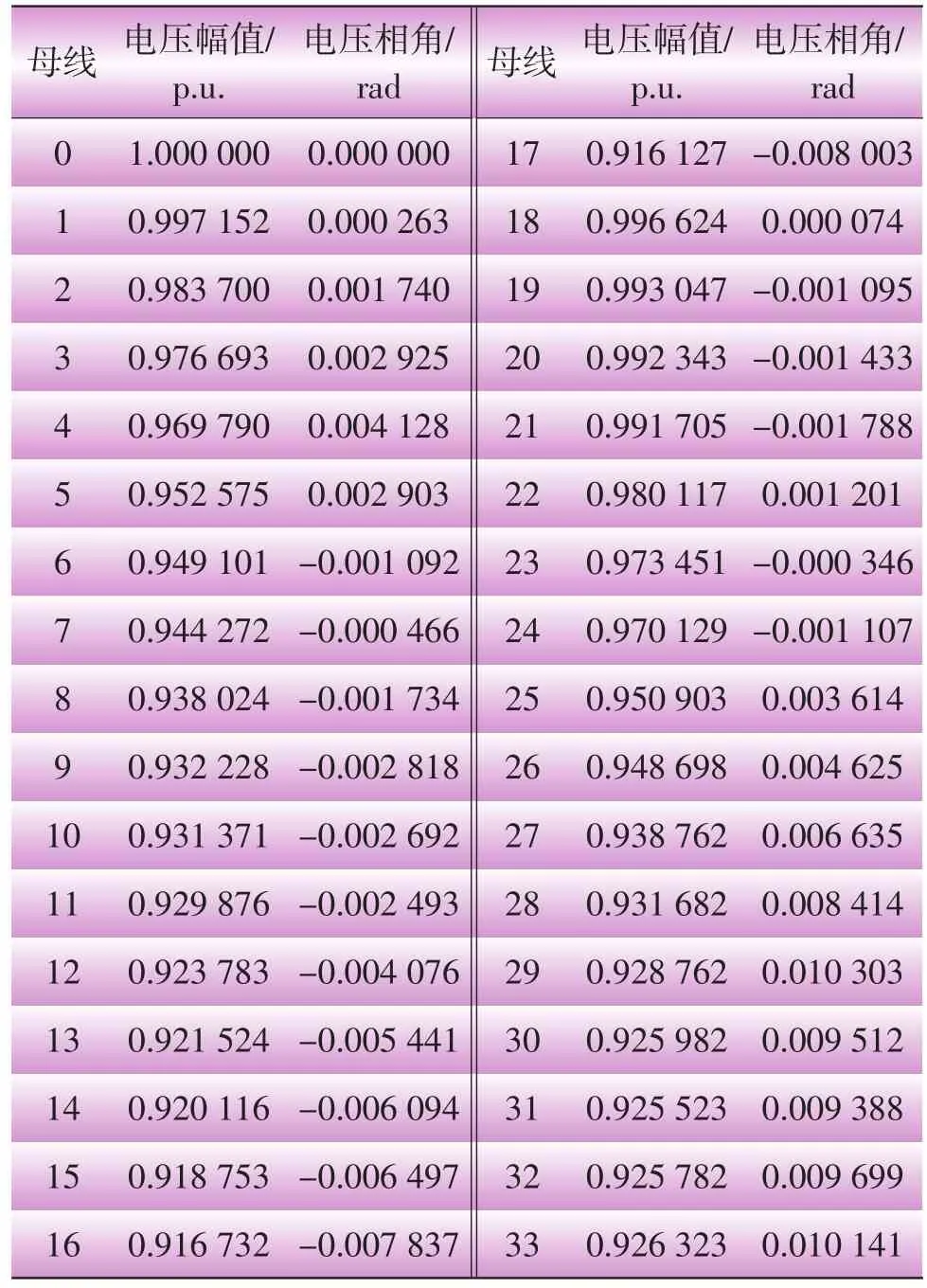
表1 单台光伏电站接入潮流计算结果
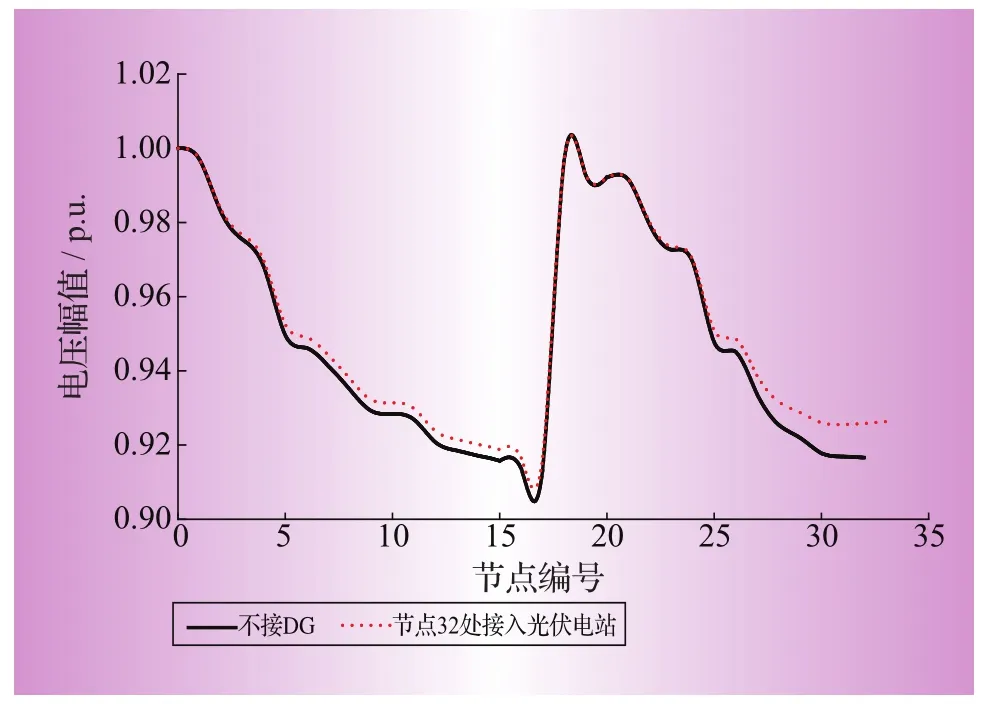
图3 节点32接入DG后的节点电压
同理,用上述方法分析在节点17处接入一台光伏电站以及在节点32和节点17处分别接入一台光伏电站之后对配电网潮流的影响,如图4所示。
分析图4可以发现,不论光伏电站是接在17号母线末端还是接在32号母线末端,系统各母线的电压都有所提高。接在主馈线17号母线的末端,对于整个系统的电压提升较高,均能达到0.92 p.u.以上;而接在分支馈线32号母线的末端,虽然能够使得该条分支馈线的电压提高得很多,但对于其他馈线(包括主馈线)的影响不是很大,对离电源点较远的母线,电压没有得到明显地提升。所以光伏电站接入配电系统,尽量在最长馈线的末端接入来改善系统电压,因为该点是整个系统电压降低最多的。
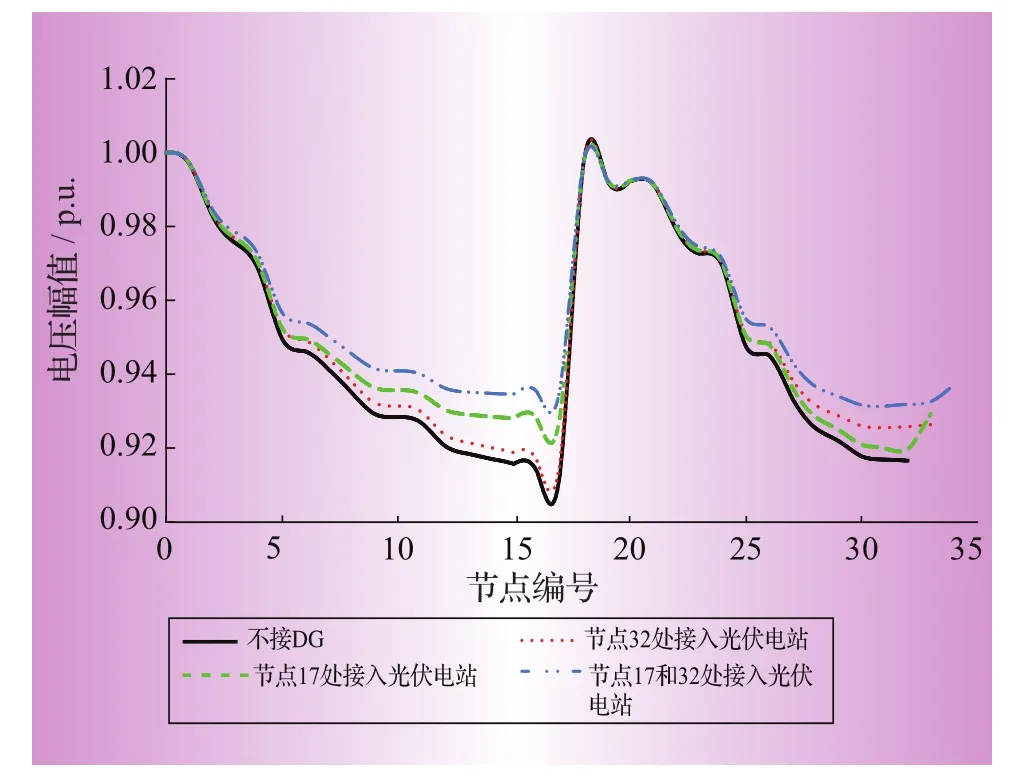
图4 DG接入配电网的不同位置对潮流的影响
2.2 不同种类DG单独接入电网对潮流的影响
不同种类的DG接在配电网同一母线处对系统电压水平的影响如图5和图6所示。
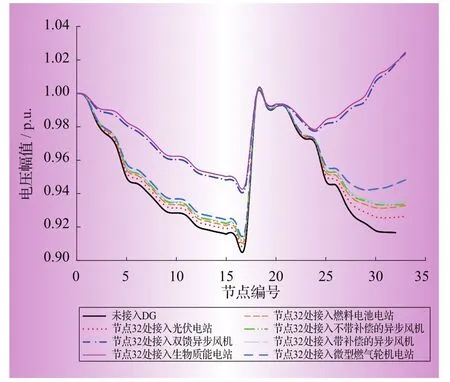
图5 节点32接入不同DG后的节点电压
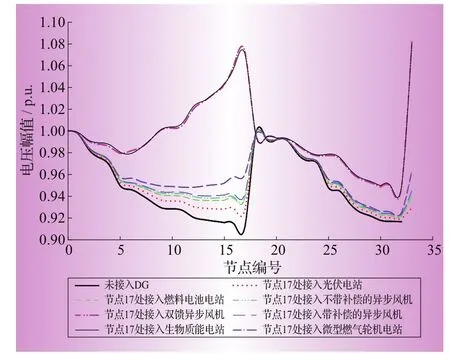
图6 节点17接入不同DG后的节点电压
燃料电池电站的接入对配电网潮流的影响,与光伏电站接入后的变化趋势大致相同。因为在潮流计算中,它们同样被视为PI节点进行处理,区别在于它们注入配电网的功率P及电流I不同,导致系统各点电压提升的高低有所差异,注入功率大则电压提升得高。
接入一台600 kW的异步风机后,分别比较有补偿电容器组和无补偿的情况,系统各母线处电压在有无功注入的情况下较没有补偿时提升得高一些,且对于风机所在的分支馈线影响较明显,对于其它分支馈线的影响不大,即无功功率的就地补偿。接在主馈线的末端时,整个系统电压水平的提升较高。
双馈异步风机的接入将接入处母线的电压抬升得很高,同时使得该分支馈线的电压也上升得很高。如果双馈异步风机接入的位置不适宜,将会使某些母线的电压越限,破坏系统的正常运行。在接入双馈异步风机时,应该综合考虑接入容量、接入位置等对于潮流的影响。
微型燃气轮机接入系统是作为PV节点处理,能提供一定的无功功率,但当无功越限时将其转化为PQ节点处理,适当将其电压范围放宽,相当于只做无功越限检查而不做电压越限检查,以保证潮流收敛。这就是图中看到的微型燃气轮机接入点的电压不等于PV节点规定的电压值的原因,即微型燃气轮机提供不了维持PV节点电压恒定所需的无功功率,从而使得电压有所下降。
接入的生物质能电站的容量为2.5MW,而系统总的有功负荷为3.715MW,因此相比其他形式的DG,生物质能电站的容量较大,同时又将其作为传统的PV节点处理,使系统各母线电压提升得非常厉害。比较接入母线17和母线32处2种情况可以看出,接入32号母线既能够有效提升系统各母线的电压,又保证了各母线电压在安全运行范围内。
2.3 多种DG接入电网对潮流的影响
在节点17处接入一台光伏电站(编号33),节点32处接入一台微燃机电站(编号34),节点21处接入一台风机(编号35),节点24处接入一台燃料电池电站(编号36),节点11处接入一台生物质能电站(编号37),节点28处接入一台带补偿的异步风机(编号38),得到的潮流计算结果(迭代5次)如表2所示,电压水平曲线如图7所示。
分析图7可以发现:混接型系统的潮流计算能够保证收敛,并且能使系统电压都有所提高,但又不至于超过电压限制,保证了系统的安全稳定。
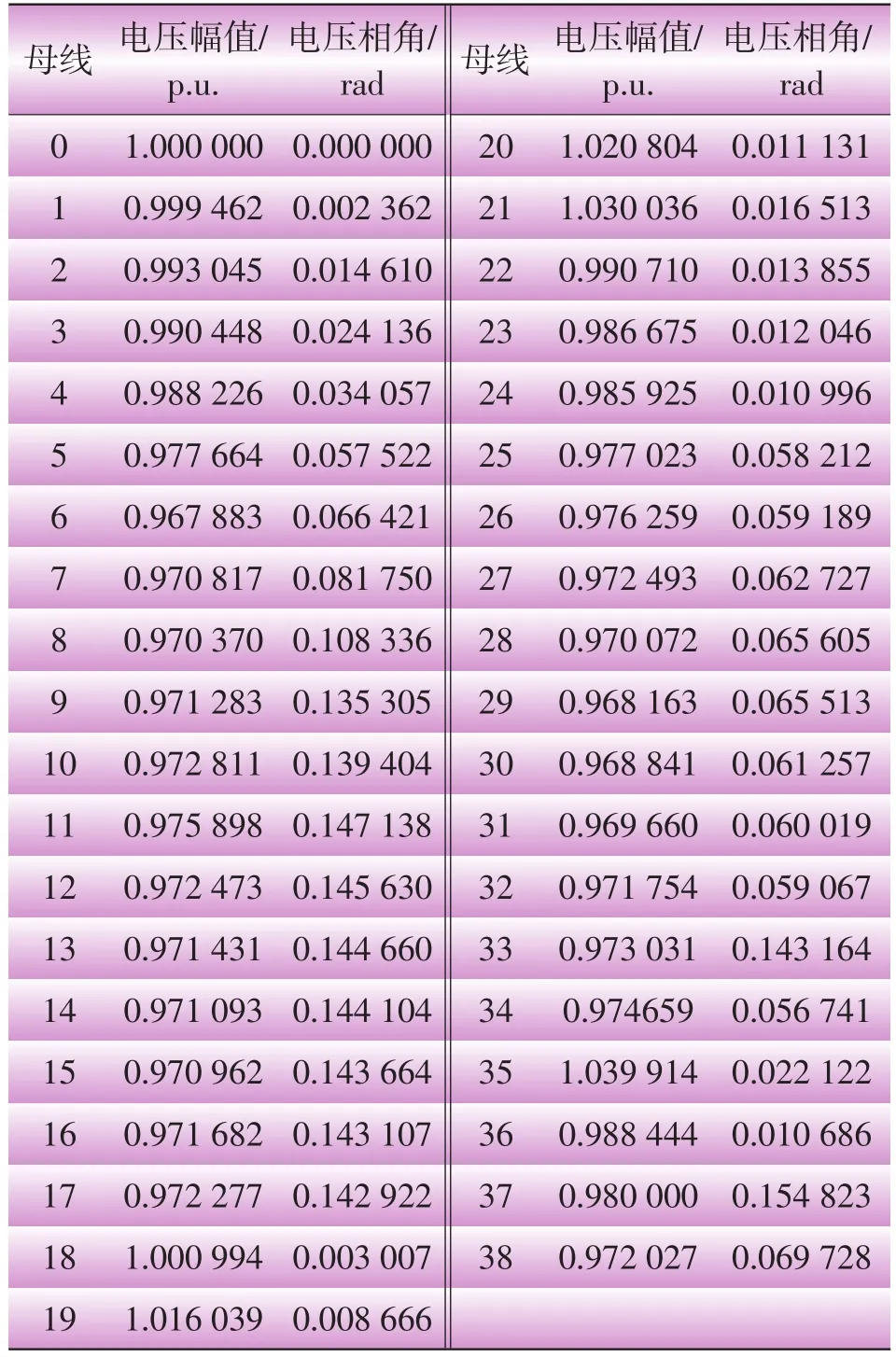
表2 混接型潮流计算结果
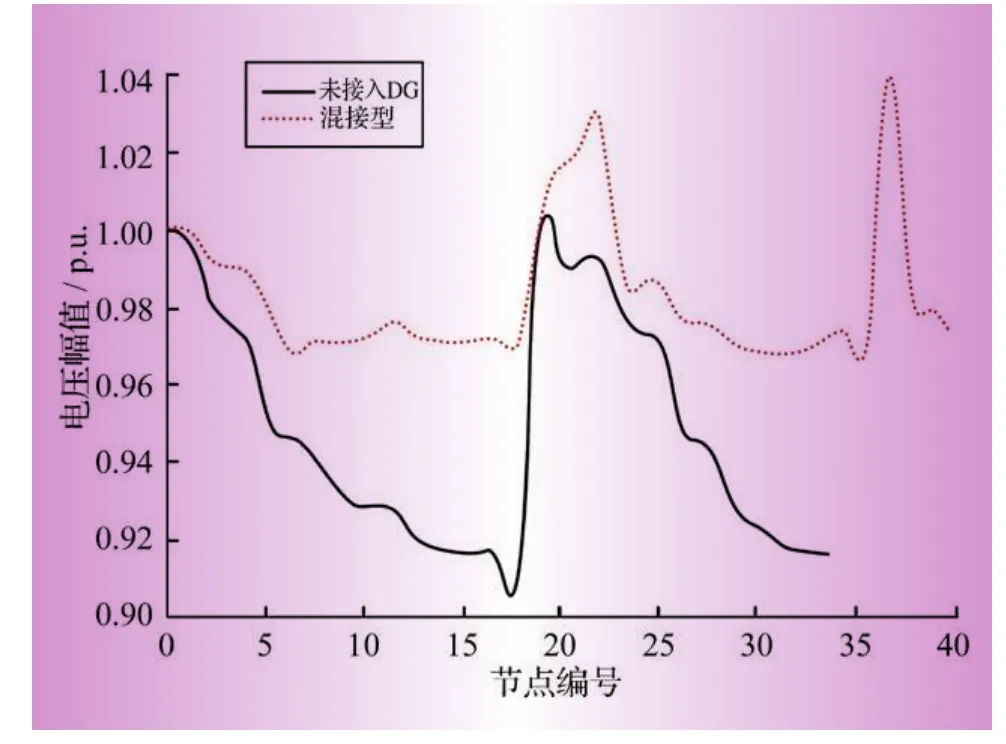
图7 混接型系统各节点电压
3 收敛特性分析
各种不同DG接入系统后,对算法收敛特性的影响如图8所示,图中纵坐标为功率误差(节点电磁功率与节点负荷功率的差值)范围,即收敛条件;横坐标为迭代次数。从图上可以看出,接入DG后迭代次数没有明显的增加,一般都能在迭代10次以内保证潮流收敛,表明牛顿法运用于含DG的配电网潮流计算是合适的。
PI型DG的接入对本算法的迭代次数影响不大,迭代次数基本不变。PQ(V)型DG,带电容器组补偿的异步风机(场)接入时,潮流迭代次数随着精度的提高而增加,对应10-8精度的迭代次数增加了4次;带变流器的双馈风机(场)接入时,类似于PI型DG,随着迭代精度的增加,迭代次数与无DG接入时的情况基本重合。PV型DG的接入对收敛性能有一定影响,在算例中最坏的情形是多迭代3次。多点混接的情况下,迭代次数相比无DG接入时最坏仅增加了3次。
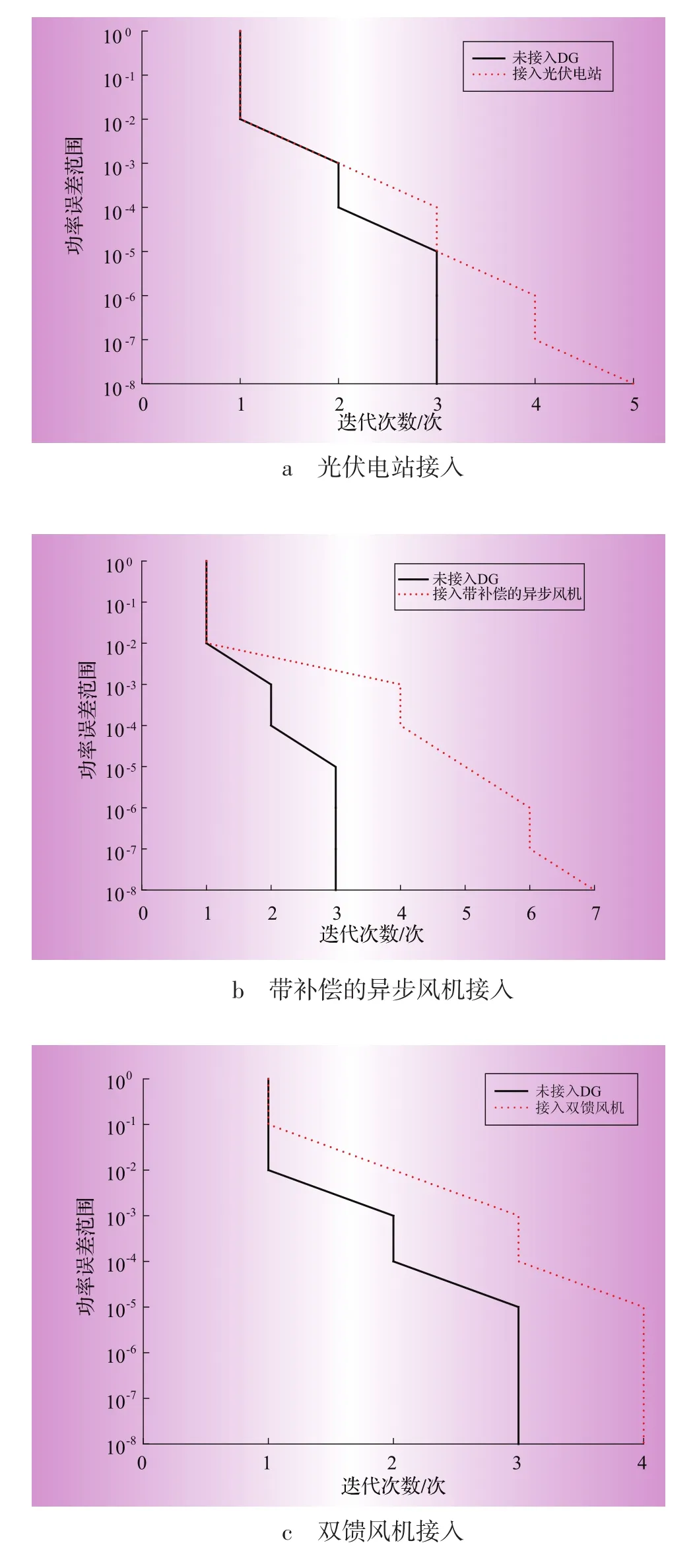
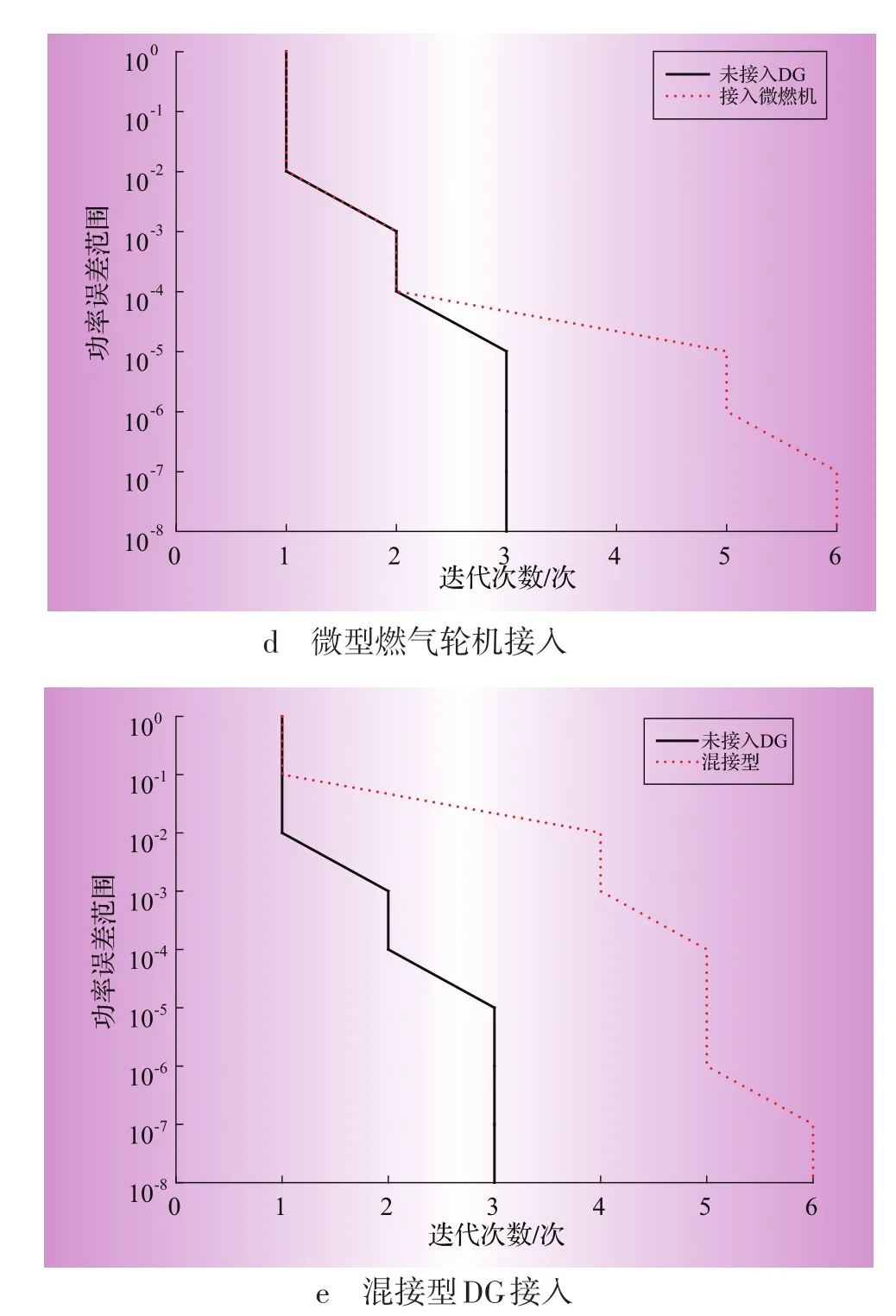
图8 不同DG接入情况下的收敛特性
4 结论
综合以上计算分析可以看出,基于牛顿法的含DG的配网潮流计算方法具有较快的收敛速度,针对各种复杂的DG类型和并网控制策略,其潮流计算结果能做到较好的收敛。
此外,DG的接入能有效抬升系统各节点电压水平,尤其是具有无功输出的DG,如:光伏电站(PI型)和微型燃气轮机电站及生物质电厂(PV型)。
[1] 殷桂梁,杨丽君,王珺.分布式发电技术[M].北京:机械工业出版社,2008:11-19.
[2] 陈海焱,陈金富,段献忠.含分布式电源的配电网潮流计算[J].电力系统自动化,2006,30(1):35-40.
[3] 郑海峰.计及分布式发电的配电系统随机潮流计算[D].武汉:天津大学,2006.
[4] 王志群,朱守真,周双喜,等.分布式发电对配电网电压分布的影响[J].电力系统自动化,2004,28(16):56-60.
[5] 赵晋泉,江晓东,张伯明.潮流计算中PV-PQ节点转换逻辑的研究[J].中国电机工程学报,2005,25(1):54-59.

