GPS长距离线性大地高与正常高比算分析

高 鹏

(吉林省电力勘测设计院，吉林 长春 130022)

GPS长距离线性大地高与正常高比算分析

高 鹏

(吉林省电力勘测设计院，吉林 长春 130022)

GPS定位技术是现代大地测量发展的重要标志，它可以直接精确地测定地面点的三维大地坐标。利用GPS定位技术所获得的三维坐标中的大地高分离求解正常高或海拔高，必须具有区域似大地水准面的成果。GPS快速、高效、高精度的技术特点，使得建立高精度高分辨率大地水准面的工作日益迫切，使其能和GPS大地高精度相匹配，实现替代水准测量的目的。

本文结合我院某工程，通过对长距离线性GPS所测得的大地高与正常高结果进行比对分析，得出平原地区，长距离带状分布测区大地高与正常高的关系。

大地高；正常高；高程拟合。

目前GPS技术已被广泛用于测量工程中，其特有的优势是传统观测手段所无法比拟的，通过GPS观测，可以精确得到二维的平面坐标，但三维的测量结果中，只能得到准确的大地高，而我们需要的是正常高，高程问题是制约GPS技术发展的瓶颈，因此我们通常用一些数学手段，将区域的GPS大地高与正常高进行转换，得到两者间的换算关系，从而将该区域的GPS大地高转换为所需要的正常高。

1 GPS高程定义

1.1 高程系统

常用的高程系统有：大地高系统、正高系统和正常高系统。

(1)大地高系统

定义：以参考椭球面为基准面的高程系统，某点的大地高是该点到通过该点的参考椭球的法线与参考椭球面的交点间的距离，也称为椭球高大地高，是一个纯几何量，与参考椭球有关，用H表示。

测量方法：大地高可以通过将笛卡尔坐标(X，Y，Z)转换为大地坐标(B，L，H)得出，采用GPS测量的方法可以直接确定出点在WGS-84地心地固坐标系下的三维坐标。

(2)正高系统

定义：以地球不规则的大地水准面(geoid)为基准面的高程系统，某点的正高是基准面(大地水准面)到该点的距离，量测沿它们之间每个等位面的垂线进行，用符号Hg表示。

(3)正常常高系统

定义：也就是我们通常所说的海拔高，以似大地水准面(quasi-geoid)为基准的高程系统，某点的正常高是该点到通过该点的正常重力线与似大地水准面的交点之间的距离，用符号Hγ表示。

(4)高程系统之间的转换关系

大地水准面到地球椭球面的距离，称为大地水准面差距，记为hg。

大地高与正高之间的关系可表示为：H=Hg+hg。

似大地水准面和地球椭球面之间的距离，称为高程异常，记为ζ。

大地高与正常高之间的关系可表示为：H=Hγ+ζ。

大地高、正高和正常高三者之间的关系见图1。

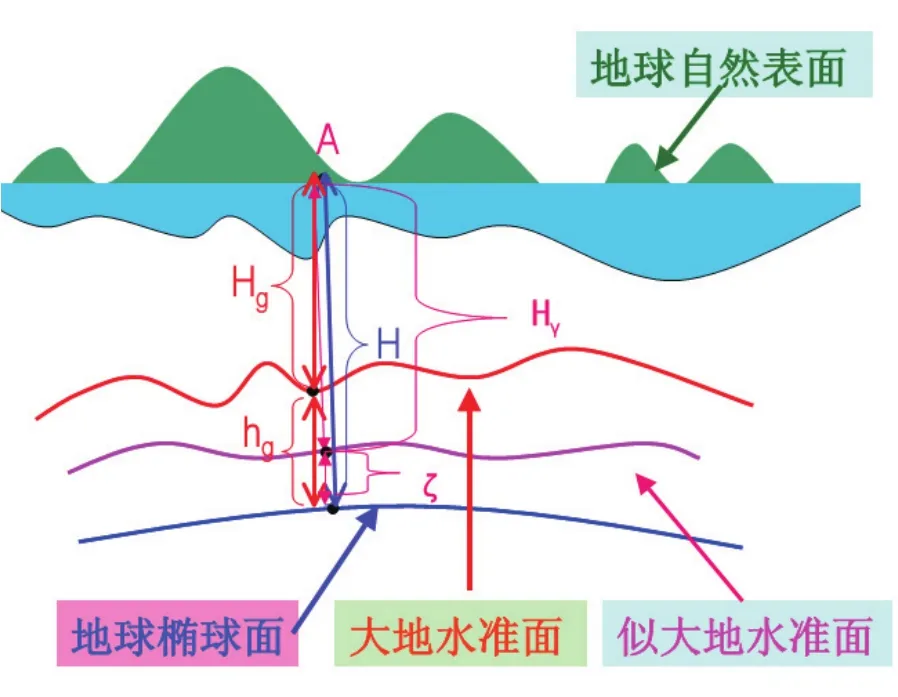
图1 大地高、正高和正常高之间关系

1.2 GPS高程的实现方法

GPS观测所得到的是大地高，为了确定出正高或正常高，需要有大地水准面差距或高程异常数据。

1.2.1 等值线图法

从高程异常图或大地水准面差距图分别查出各点的高程异常ζ或大地水准面差距hg，然后分别采用下面两式可计算出正常高Hγ和正高Hg。

正常高：Hγ＝H -ζ， 正高：Hg＝H-hg

在采用等值线图法确定点的正常高和正高时要注意以下问题：

(1)等值线图所适用的坐标系统，在求解正常高或正高时，要采用相应坐标系统的大地高数据。

(2)采用等值线图法确定正常高或正高，其结果的精度在很大程度上取决于等值线图的精度。

1.2.2 地球模型法

地球模型法本质上是一种数字化的等值线图，目前国际上较常采用的地球模型有OSU91A等，不过这些模型均不适合于我国。

1.2.3 高程拟合法

所谓高程拟合法就是利用在范围不大的区域中，高程异常具有一定的几何相关性这一原理，采用数学方法，求解正高、正常高或高程异常。

1.2.4 区域似大地水准面精化法

精确求定区域大地水准面是大地测量学的一项重要科学目标，也是一个极具实用价值的工程任务。

高精度、高分辨率大地水准面的确定，其主要目的是：用GPS定位技术结合区域内的地面重力资料、水准资料、高分辨率的地形数据以及最新的重力场模型，精确地研究并确定区域似大地水准面，以求取高精度的高程异常值，从根本上解决GPS定位技术无法直接提供正常高(海拔高)的问题。

1.3 高程拟合的常用方法

一般有多项式拟合法、多面函数拟合法及分区拟合法等。

多项式拟合法主要是利用公共点上GPS测定的大地高和水准测量测定的正常高计算出该点上的高程异常ζ，利用这样的公共点，n个公共点则列出n个方程，其权阵根据水准高程和GPS所测得的大地高的精度来确定。

多面函数拟合法基于以下观点：任何一个圆滑的数学表面总可用一系列的有规则的数学表面的总和以任意精度逼近。

多项式拟合法和多面函数拟合法都是纯几何的方法，因此，一般仅适用于高程异常变化较为平缓的地区(如平原地区)，其拟合的准确度可达到一个分米以内。但对于高程异常变化剧烈的地区(如山区)，这种方法的准确度有限，这主要是因为在这些地区，高程异常的已知点很难将高程异常的特征表示出来。这种情况则可通过选择合适的高程异常已知点及提高已知点数量，再采用上述方法，或才采用分区拟合的方法，将整个测区按地形特征进行分区，再作拟合。

2 工程实例

2.1 测区状况

该测区位于我国北纬123°50′，东经45°30′左右，控制点全线总长为158.4km，直线长度为142.3km。地形特征为平原地区，部分地段林木茂盛，交通良好。

2.1.1 GPS观测方法

GPS观测前了解卫星分布情况，选择较好时间段进行外业观测，观测时均满足如下要求：

①观测前应准确对中，确保对中误差不大于3mm；

②观测组必须严格按照规定的时间进行作业，同步观测同一组卫星；

③作业过程中，天线高在测前和测后各量测一次，两次量测差值小于3mm，取其平均值参与计算；

④接收机开始记录数据后，观测员查看测站信息了解观测情况，即时调整观测时间和观测位置。

2.1.2 GPS网观测

施测中基准点与基准站、基准站与国家控制点之间的联测时间不少于60min，主要技术参数见。相邻两天间的数据联测至少要联测两个以上的基准点。整个控制网以基准点为主导线点，布置成了附合导线。测区所有点位分布见图2。

表1 GPS网观测主要技术参数

图2 测区所有点位分布平面图

3.2 解算结果分析

以首级控制SYBA、SYBC、LMGT和D024四点，沿整个线路路径计算出其概略高程异常值 ，以该拟合结果，计算其他首级控制点，其计算结果与实测正常高比对，误差优于0.05cm。结果见表2、表3、图3、图4、图5。

表2 解算结果

表3 基准点

图3 高程异常值分析

图4 正常高与大地高比对分析

图5 解算精度分析

4 结论

(1)平原地区长距离线性测量中，控制点沿线路均匀分布，其高程拟合效果较为理想，由本文的工程实例可以看出，线路中各点的Rms均小于5cm，Rms平均值为2.4cm，最大值为4.8cm，最小值不到1mm。

(2)该地区的高程异常值变化较为均匀，自东向西逐渐减小，其变化趋于线性，从理论上说，该地区似大地水准面变化与该变化曲线相近。

(3)控制点分布理想，则平原地区的GPS高程代替传统水准传递，其效果比较理想，可以大大减少外业工作强度。

(4)若结合重力数据，则可以很好的推算该地区的似大地水准面。

[1]刘基余．GPS卫星导航定位原理与方法[M]．北京：科学出版社，2003．

[2]李征航，黄劲松．GPS测量与数据处理[M]．武汉：武汉大学出版社，2005．

[3]周忠谟，易杰军，周琪．GPS卫星测量原理与应用[M]．北京：测绘出版社，1992．

[4]王惠南．GPS导航原理与应用[M]．北京：科学出版社，2003．

[5]刘基余，李征航，等，全球定位系统原理及其应用[M]．北京：测绘出版社，1993．

[6]魏子卿，葛茂荣．GPS 相对定位的数学模型[M]．北京：测绘出版社，1998．

Analysis on Linelyheight and Normal Rate in Long Region by GPS

GAO Peng
(Jilin Province Electric power Survey and Design Institute, Changchun 130022, China)

The GPS position technology is the modern geodetic survey development important symbol, which can survey decide the ground three dimensional geodetic coordinates directly and precisely. The ellipsoidal height in the three dimensional coordinates obtains which using the GPS position technology solves normal height or the elevation height by separation, must have the achievement of region to the geoid precision. The fast, highly effective,high accuracy technical characteristic of GPS, causes the work to establish the geoid precision high accurately and high resolution to be day by day urgently, enables its to match with the GPS accuracy ellipsoidal height, realization substitution level survey goal.

This thesis integrates a project in my partment , analysises the ellipsoidal and the normal height linely in long region which obtained by GPS .At last , this thesis obtaines the relation in the ellipsoidal.and the normal height linely in long region.

ellipsoidal; normal heiht; height fi tting.

P2

B

1671-9913(2011)03-0015-04

2011-03-30

高鹏(1982- )，男，吉林桦甸人，硕士，主要从事GPS技术的应用等工作。