湖南省似大地水准面模型对比研究

摘" 要：正常高系统是以似大地水准面为基准的高程系统，也是中国目前采用的高程系统。随着GNSS定位技术的广泛应用，已能在10-7～10-9的精度量级上获得测量点的平面位置，但是却一直未能以相应的精度求解点的高程值。因此，通过建立高精度、高分辨率的区域似大地水准面模型提升高程测量的精度，成为重要的技术手段。该文通过对湖南省2007似大地水准面模型后期各似大地水准面模型的对比研究，找到模型的差异，并对差异较大的地区进行特征分析，查找形成差异的原因，可为全省二、三等水准网测量和大地水准面再精化工作提供参考。

关键词：大地水准面;高程异常;似大地水准面模型;等值线图;模型对比

中图分类号：P224" " " 文献标志码：A " " " " " 文章编号：2095-2945（2024）26-0109-04

Abstract： The normal height system is an elevation system based on the quasi-geodetic level， and it is also the elevation system currently used in China. With the wide application of GNSS positioning technology， the plane position of the measuring point can be obtained in the order of the accuracy ranging from 10-7 to 10-9， but the elevation value of the point has not been solved with the corresponding accuracy. Therefore， it has become an important technical means to improve the accuracy of elevation survey by establishing a regional quasi-geoid model with high precision and high resolution. In this paper， through the comparative study of the quasi-geoid models in the later stage of the 2007 quasi-geoid model in Hunan Province， the differences of the models are found， and the characteristics of the areas with great differences are analyzed to find out the reasons for the differences， so as to provide reference for the second and third order leveling network survey and geoid re-refinement in the whole province.

Keywords： geoid; height anomaly; quasi-geoid model; isoline map; model comparison

众所周知，大地水准面是描述地球形状的一个重要物理参考面，它也是海拔高程系统的起算面。似大地水准面是从地球表面点沿正常重力线量得的正常高所得端点构成的封闭曲面，它接近于水准面，与大地水准面不完全吻合。似大地水准面是测量计算的辅助面[1-2]。

1" 2007模型

2007年，湖南省参与了华东、华中区域似大地水准面精化工作，通过卫星定位测量、水准测量及重力测量，建立了国家大地基准控制和省级基础控制网，形成的成果具有高精度、三维和多功能特点，利用近3万个地面重力观测资料，基于EGM96全球重力场模型，采用Molodensky原理移去-恢复获得重力似大地水准面，如图1所示。将其拟合适配于省内559个A、B、C级GNSS水准控制点，取得了分辨率2.5′×2.5′的似大地水准面模型（以下简称“2007模型”），通过27个检核点获得其外符合检测精度为±0.043 m;并获取了似大地水准面模型[3-4]。该模型为湖南省历史上第1个省级似大地水准面模型，其建设的主要目的是为满足1∶10 000和1∶5 000测图的需求，同时为市、州级似大地水准面模型的建立奠定基础。

2" HNQG2013模型

利用高分辨率3″×3″数字高程模型、1′×1′空间重力异常格网模型和地球重力场模型，采用地形均衡归算、移去-恢复原理计算重力似大地水准面。似大地水准面模型如图2所示。

3" 2017模型

2007湖南省似大地水准面模型，在一定程度上存在精度有限、空间分布不均匀的局限。该模型在GNSS水准点较密（点位距离小于10 km）的平原地区，精度较高，可达2～3 cm，但在GNSS水准点较稀少（点位距离在20 km左右）以及丘陵区和拔高的山区，似大地水准面的精度只能达到±5～10 cm，甚至更差。限于当时的技术，平原和山区大地水准面精度相差较大。另外，由于采用分区拟合，不但造成区与区之间可能存在系统差，而且离已知点越远的地方，精度也会较差，难以满足经济发展和城市信息化的要求，所以有必要重新确定高精度的似大地水准面模型。针对水准面模型所存在的问题，湖南省进行了精化，利用已有的近7万个湖南及邻近省份重力观测数据、502个GNSS水准控制点及数字高程模型，以EIGEN-6C4全球重力场模型作参考重力场，采用顾及地球曲率影响的各类地形质量位及引力的第二类Helmert凝集法严密算法，利用高分辨率地形数据恢复甚短波扰动重力场，确定空间分辨率2′×2′的高精度湖南省似大地水准面模型（HNGG2017），以下简称2007模型。经外部检核，模型整体精度均优于±0.022 m。

4" 2007模型和HNQG2013模型对比分析

通过2007模型图（图1）和2013模型图（图2）对比可知，其主要差别如下。

1）HNQG2013在建模方法上，舍弃了十参数多项式、多面函数等方法;

2）HNQG2013具有完整的6°×6°范围，但HNQG2007因边缘变形切除而不完整;

3）HNQG2013采用1′×1′分辨率，而HNQG2007采用2′30″×2′30″分辨率;

4）HNQG2013不存在粗差问题区域，HNQG2007存在低精度区域;

5）HNQG2013短波信息比HNQG2007信息更丰富，模型精度更高。

重力大地水准面与GNSS水准之间的差异如图3所示。

对2套模型之间的差值进行比较，2个模型最大的差值在局部地区达到0.8 m，在湖南省边缘地区普遍有分米级的差异，差异的形态呈椎形分布。

将不同地区的差值以数字进行标注，较清晰地反应了差异的地理分布状况。差异产生的原因一是建模方法的不同，二是所利用的数据可能出现粗差。多项式拟合存在龙格现象，次数越高的多项式拟合曲面时多余摆动越大，湖南省边界之外的GNSS水准控制点很少，采用多项式拟合的方法会造成很大的变形;而多面函数方法在国际上早已经被否定，因为其光滑因子很难高精度地由人工确定，并可能会导致曲面形成严重的椎状变形。HNQG2013建模中摈弃了上述两者方法，而采用最小二乘原理及最小曲率样条方法，理论上可获得更高的精度。

5" 2007模型和2017模型对比分析

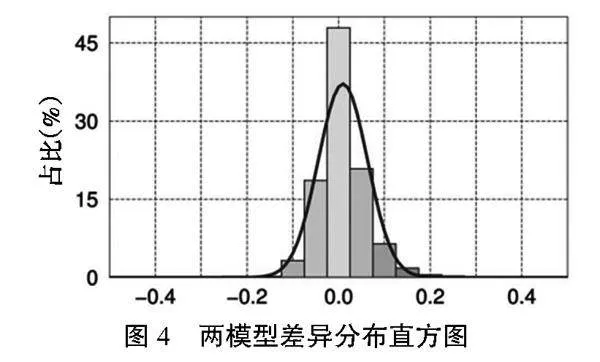
在整体趋势方面，2007和2017两个版本的模型是一致的。在湖南省北偏西、东南、西南等边界处2期模型有相对较大的差异，在湖南偏北部可以明显看到一个凸起，差异可达到0.5 m。整个差异的平均值0.009 m、最大值0.507 m、最小值-0.169 m及RMS值0.054 m。各个点差异分布的直方图如图4所示。

从图4可以看出，各个点的差异分布主要集中在[-0.15，0.15]m的区间内，只有约0.2%（9个点）的差异值超过0.3 m， 0.6%的差异值超过0.2 m且小于0.3 m，超过99%的点的差异值均分布在±0.2 m以内。通过2017模型和2007模型的对比分析，可能存在粗差的控制点，设置了5个特殊点位，用于进一步验证模型的准确性[5]。

2017版模型与2007版模型差异较大点位于常德市汉寿县和永州市江永县桃川镇。实验数据表明，卫星定位测量的结果和水准测量的结果与原控制点的成果一致，高程异常分别为-19.188 m和-17.036 m，与2017版高程异常差分别为3.0 cm和9.4 cm，与2007版模型高程异常相比相差分别为16.0 cm和41.1 cm。这说明了汉寿地区，2017模型是正确的。2007模型与实测高程异常差异较大的原因，模型建立过程中，可能引用了不准确的数据，或者模型自身的拟合过程存在一定的问题;边界处数据不足可能导致2007年模型在边界处高程异常计算不准确。2007年采用的拟合方法构建似大地水准面模型主要依赖于GNSS水准点的分布精度，且模型精度不均匀，在缺乏已知点或已知点出现偏差的区域精度较低。江永区域没有GNSS水准点[5-6]。相比之下，2017模型更多的依赖地面和卫星重力观测数据，在缺乏控制点的情况下，其更能真实客观地描述水准面的特征。该控制点距离最近的水准起算点距离超过40 km，按照国家二等水准测量规范，随机误差达到±4 cm（±1 mm/km）。实测成果与2017模型相差9.4 cm，可能是水准测量精度不足所致。

2017版模型与控制点差异较大的点位于常德市石门县壶瓶山镇、湘西自治州龙山县和永州市双牌县茶林镇[5-6]。位于湘西州龙山县一个点的实测数据成果的高程异常为-25.771 m，仅与2017模型相差约1 cm，与控制点高程异常相差6.5 cm。该点位于湘西龙山县，由于该点重力水准面与正常高差异较大，达到9 cm，该控制点可能存在粗差。实测所得的大地高与控制点的大地高相差5.8 cm，实测正常高与控制点正常高的差距仅为0.7 cm，实测高程异常与2017模型高程异常差为0.9 cm，与模型较为符合。造成两期卫星定位测量结果的差异达到5.8 cm，对比分析其原因可能如下。

1）该控制点布设时间较长，10多年前因当时的仪器设备、卫星数量等原因，可能会使得其测量精度比当前测量精度低。

2）当时的卫星定位测量过程中，天线高的量取不够准确，或者数据处理过程中，天线高模型不匹配或者与基准站基线过长所致。另一点位于永州市茶林镇，结合外部精度检测，该点的模型高程异常与控制点高程异常差异较大，远大于3倍中误差。实测结果表明，该点的高程异常为-16.097 m，与2017模型的-16.078 m相差1.9 cm，与2017模型较为符合。该点的实测大地高与控制点大地高差为16.5 cm，两者的差异较大，超过限差要求，该点的实测正常高与控制点正常高差为0.6 cm，差异较小。造成两期大地高差异较大的原因与前一点较为相似。该点位于常德市壶瓶山镇，通过实验，结果表明，该点的实测大地高与实测正常高均与控制点大地高、正常高差异较小。该点的实测高程异常与2017模型的高程异常差达到了17.3 cm，差异较大。对比分析，其差异较大的原因可能为以下几点。

1）壶瓶山为山区，地形起伏较大，DEM的精度较低，2017模型在该地区可能精度较低。

2）该地区重力数据较为稀少，也有可能造成2017模型在该地区精度较低。

3）该地区由于地形起伏较大，可能造成水准测量精度较低。

为了进一步验证2017模型的准确性，从被剔除的 点以及壶瓶山区域内差异较大的点，选取了部分点进行特殊点位检核。

特征点位检核主要是针对2017版模型与2007版模型差异较大的点位、残差较大的控制点和某一区域模型整体差异较大的点位这3类特殊点位进行实地测量，进行精度检核。通过特征点位的检核，进一步验证模型和控制点的准确性。

1）点位选取。针对以上3 类点位的定义，点位的选取标准为2007和2017湖南省似大地水准面模型差异较大的位置为第1类;点位于模型高程异常和控制点高程异常差异较大（一般为±9 cm以上）的位置为第2类;点位于控制点和2017模型高程异常存在系统性差异的区域为第3类。选取了同一条水准路线上的1对点位，以其中一个点假设认为模型高程异常正确，另一个认为控制点或高程异常错误。

2）数据采集。数据采集采用外业测量的形式，包括GNSS和水准测量。GNSS测量参照不低于GPS测量规范C级GNSS网的要求进行;水准测量参照二等水准测量进行。连续观测8 h以上，与周边HNCORS基准站联测;水准测量时仪器设备及观测参照二等水准测量规范执行，考虑线路距离较短、纬度差异小、点位之间高差较小，尺长改正、水准面不平行和重力改正数值特别小，给予忽略。

3）模型高程异常计算。依据GNSS水准控制点的坐标，高程异常通过2017湖南省似大地水准面模型计算得到。

4）计算控制点的高程异常。控制点的高程异常用实测大地高和实测正常高来进行计算。

5）分析研究对控制点高程异常和模型高程异常的差进行统计分析。统计分析通过最大值、最小值、平均值、均方根和标准差5项指标予以呈现。

通过分析发现，在壶瓶山区域，中部和北部偏差为6～8 cm（其中U004达13 cm）。该地区的差异呈现出系统性特征。考虑到2017湖南省似大地水准面模型是统一处理的，且通过外部精度检测发现2017湖南省似大地水准面模型精度达到了2 cm，不太可能出现局部超过6 cm的偏差。同时，从建模方法上分析，在距离相近的2个点不太可能存在一个点与2017模型符合较好而另一个差异较大的情况。进一步分析可知，差异较大的点均分布于Ⅱ杨石线附近，这些点均是以Ⅱ杨石线上的二等水准点作为起算点。因此，我们推测，可能是水准起算点存在一定的偏差。若是水准起算点存在一定的偏差，通过常规的方法是难以检测出来的，故采用测量高程异常差的方法来进行检核。具体方法如下，采用水准和卫星定位测量联测一个与2017湖南省似大地水准面模型符合较好的点和一个似大地水准出现较大偏差的点，通过模型计算出2个点的高程异常差，对比实测的高程异常差，来确认该区域究竟是由于水准起算引起的控制点不准确，还是由于模型本身存在问题。

2017湖南省似大地水准面模型在U**3点符合较好（差异为2.7 cm），而在U**4点的差异达到了8 cm。采用水准测量方式联测U**3和U**4获取其正常高差，同时采用卫星定位测量方式联测这2个点获取其大地高差。其中卫星定位测量参照C级GNSS的标准，对U**3、U**4点进行同步观测，水准测量参照二等水准测量标准，测量其正常高差。

通过对比实验，这2个点的实测高程异常差为0.288 m，它与控制点高程异常差相差6.4 cm，与2017模型的高程异常差相差1.4 cm，符合较好。导致这种现象产生的原因可能如下。

1）在这2个点上，水准测量的精度标准不一致。控制点正常高测量是按照三等水准测量标准，而本次正常高差测量参照二等水准测量标准，精度较高。

2）在差异较大的壶瓶山区域，水准测量的起算点的精度或许存在问题。

6" 结论

1）成果在分辨率和精度2方面均符合国家技术标准的要求;

2）2017模型整体精度优于2.5 cm，平原、丘陵地区优于2 cm，山地优于4 cm，达到了技术设计书的要求。通过与2007模型对比以及实际测量，可以得出结论，2017模型相对于2007模型在常德汉寿地区、永州江永地区，精度得到了明显的改善。此外，通过特殊点位检核，我们发现，个别C级点存在较大的误差，建议在今后的工作中，对与2017模型差别较大的控制点进行复测，以保证控制点的准确性。在壶瓶山区域，水准起算点可能存在一定的问题，在今后的工作中，需要采用更高等级的水准测量，进一步确认壶瓶山区域的水准起算点的准确性。

参考文献：

[1] 宁津生，罗志才，李建成.我国省市级大地水准面精化的现状及技术模式[J].大地测量与地球动力学，2004（1）：4-8.

[2] 李斐.大地测量基础理论与方法研究进展[J].地球物理学进展，2000（2）：63-66.

[3] 唐秋祥，伍百发.省级似大地水准面的局部再精化[J].测绘科学，2013，38（4）：7-9.

[4] 刘鹏程，戴建清，匡志威.长沙市高精度似大地水准面模型的确定[J].城市勘测，2014（1）：113-126.

[5] 董明旭，李建成，华亮春，等.湖南省似大地水准面2017模型及精度分析[J].大地测量与地球动力学，2019，39（1）：66-71.

[6] 李明飞，吴军超，秦川.基于移去-恢复法的局部似大地水准面精化模型对比研究[J].大地测量与地球动力学，2020，40（9）：952-956.

基金项目：2022年湖南省自然资源科技计划项目（2022G19）

第一作者简介：喻艳梅（1965-），女，副教授。研究方向为GNSS测量、数字测图等。