货物列车编组计划与编组站负荷分工联合优化模型

耿令乾

（沈阳铁路局 运输处，辽宁 沈阳 110001）

货物列车编组计划与编组站负荷分工联合优化模型

耿令乾

（沈阳铁路局 运输处，辽宁 沈阳 110001）

提出编组站解编负荷状态评价函数及曲线，以车流组织费用最小化和编组站解编负荷状态最佳化为目标，构建货物列车编组计划与编组站负荷分工联合优化模型，并考虑编组方案惟一性、解编能力和调车线数量等约束条件。利用目标规划法(GP)将模型由多目标转化为单目标，设计了相应的搜索生成方法并编程予以实现。最后基于实际路网案例，使用LINGO数学软件完成模型的求解和对比分析，验证了模型的合理性和有效性。

铁路；编组站；编组计划；优化模型

1 研究背景

随着我国高速铁路的建设，既有线货运能力得到释放，铁路大货运量时代即将到来。铁路编组站是运输生产的核心部门，其负荷状态对全路运输组织效率和效益产生影响，如何充分利用编组站的有效能力、降低车流组织成本是亟待研究解决的重要问题之一。货物列车编组计划决定了车流的解编作业地点，与编组站的负荷分工有密切的关系，同时编组站的负荷程度又会影响编组计划的编制和实施，因此有必要将两者联系起来共同研究，以实现车流组织和编组站负荷分工的双赢局面。

一些专家和学者在车流组织和编组站布局方面进行了深入研究[1-5]，并取得了丰硕的理论成果。但是，尚未有研究对货物列车编组计划与编组站负荷分工进行联合优化。本文提出编组站解编负荷状态评价函数，以车流组织费用最小化和编组站负荷状态最佳化为目标，构建货物列车编组计划与编组站负荷分工联合优化模型 (A)，采用目标规划法 (GP)将其转化为单目标模型，设计了车流组合变量fij的搜索生成方法，并利用 LINGO 数学软件实现了模型的求解和对比分析。

2 编组站解编负荷状态评价函数及曲线

每个编组站都存在最佳的解编负荷状态，当解编负荷量较小时，其设备能力未充分利用，致使单位车辆的解编成本相对增加；反之，若解编负荷量过大，则易造成车流等候，加速设备折旧，削弱特殊事件的应对能力等。为此，提出编组站解编负荷状态评价函数S(Wi)，用以描述负荷需求与能力供给之间的匹配程度，其中Wi表示i站的实际解编负荷量。定义编组站i的解编设计能力为，对应的解编负荷量为，有：

假设存在某个最佳的解编负荷量，既可以充分发挥编组站的有效能力，又能保证站内车流作业有序、压缩解编成本，使编组站处于最佳负荷状态。与编组站的众多复杂因素有关，通常需要预留一部分能力以应对特殊情况 (如车流波动等)。若编组站的实际解编负荷量与有效能力相匹配，则在理论上可认为其已达到最佳负荷状态。定义i站的弹性扣除系数为αi，有：

利用Smax表示编组站解编负荷状态的最佳值，对应的关系曲线如图1所示。

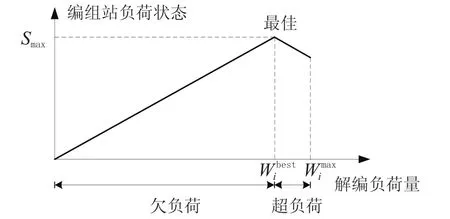
图1 编组站解编负荷状态曲线

当解编负荷量Wi未达到时，编组站处于欠负荷状态，随着解编负荷量的增加，负荷状态曲线单调上升，斜率为k欠负荷，即在区间 (0，) 上编组站的负荷状态逐渐提高。当解编负荷量达到时，编组站处于最佳负荷状态。当解编负荷量超过后，虽然未突破编组站的设计能力，但已经开始占用预留能力，编组站处于超负荷运转状态，车流等待和设备损耗成本逐渐显现，因此编组站解编负荷状态曲线在区间 () 上呈递减趋势，斜率为k超负荷。k超负荷的效果近似于惩罚系数，涉及因素较为复杂，不妨暂设k超负荷＝－k欠负荷，以便于后续的计算和分析。

综上所述，编组站解编负荷状态评价函数可表述为：

3 货物列车编组计划与编组站负荷分工联合优化模型

3.1 参数和变量说明

设路网结构N＝(P,E)，其中P为技术站集合(含编组站)，P＝{1,2,…,n}，E为路段集合，E＝{eij|i，j∈P}；lij表示i→j径路上的途经技术站集合(设OD车流径路已知且惟一)，lij⊂P；Ci为i站的集结系数 (h)；mij为i→j去向的平均编成辆数，与途经区段的牵引定数有关(车)；ti为单位车辆在i站的解编作业时间消耗 (h)；Hi为i站调车场线路总数(条)；fij为i→j的车流总量 (车)。

定义直达去向决策变量：

3.2 目标函数

（1）车流组织费用最小化。从优化货物列车编组计划的角度出发，以组织直达去向的集结车小时消耗和车流在途中解编车小时消耗最小化作为模型的目标函数：

（2）编组站解编负荷状态最佳化。采用编组站解编负荷状态评价函数即公式⑶描述各编组站的负荷状态，以路网上所有编组站的解编负荷状态最佳化为目标：

公式⑺促使负荷不足的编组站吸引车流，负荷过量的编组站转移车流，直接影响列车编组计划的生成。考虑到公式⑶中S(Wi) 为分段多项函数，在计算求解的过程中效率较低，因此将其简化为：

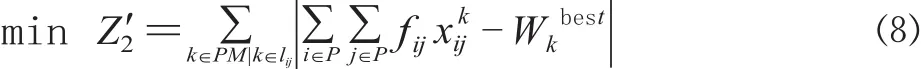
式中：可理解为编组站负荷程度的期望值，实际解编负荷与期望值的偏差越小，表明编组站的负荷状态越理想。

3.3 约束条件

（1）编组方案惟一性约束。对于任意车流fij，只能选择一种组织方案，编开直达列车或并入近程去向在k站进行解编作业，即：

（2）车站解编能力约束。无论是编组站还是技术站，都存在解编能力上限，实际的解编作业量不得超过车站的最大解编能力，即：

（3）调车线使用数量约束。编组列车所使用的调车线数量应小于上限，每个编组去向至少占用一条调车线。设调车线的单位容量为ω车，有：

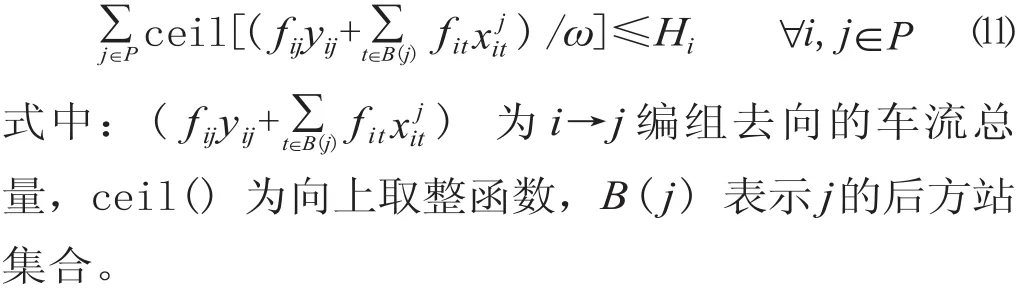
（4）车流合并、解编的前提条件约束。若车流fij选择在途中k站进行解编作业，则前提是存在i→k的近程直达去向。换言之，当i→k直达决策变量yik＝0 时，必有＝0；反之，若yik＝1，此时＝0 或 1，线性不等式可表述为：

根据0-1变量的特性，同一近程去向的约束条件相互叠加形成：

式中：N为一个足够大的正数。

（5）变量类型约束。决策变量yij、均为 0-1变量：

3.4 构建模型

综上所述，以车流组织总费用最小化作为第一目标，以编组站解编负荷最佳化作为第二目标，构建货物列车编组计划与编组站负荷分工联合优化模型 (A) minZ1，Z2′。模型(A)属于多目标 0-1 整数规划模型。

4 求解流程及相关方法说明

4.1 模型求解流程

首先利用 VC++ 程序将fij表述为车流 OD 和决策变量xijk的组合形式，然后基于目标规划法 (GP)将模型 (A) 的多目标函数转为化单目标函数，并使用 LINGO 软件结合具体案例对模型 (B) 求解，优化确定列车编组计划和编组站解编负荷分工方案。

4.2 基于车流径路的 fij 搜索生成方法

铁路车流属于一种强可控交通流，运输过程中呈现出树形径路、不可拆分等特点[6]。在技术站完成解编作业后的车流，如果有相同的前方到站，即视为同一支车流，在送往目的地的过程中不能被拆散。由i→j的总车流fij的表达式为：

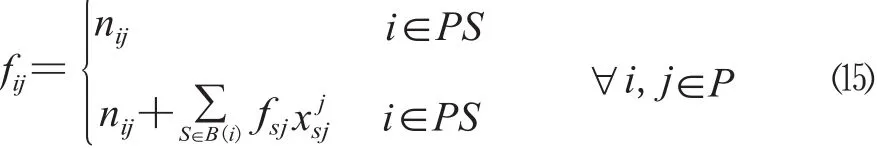
不难看出fij的表达式涉及组合嵌套，其复杂程度呈级数增长，难以直接表述。因此，通过设计基于车流径路的fij搜索生成方法，结合VC++ 程序设计予以实现。其步骤扼要说明如下。

步骤 1：已知集合N＝{nij|i，j∈P}中各OD对应的惟一径路，车流n00的径路可描述为l＝{O，

ODOD k1，k2，…，km，D}，其中O、D分别为起讫点，k1，k2，…，km为途经技术站，依次类推生成全体OD 的径路集L。

步骤 2：欲确定车流fij的表达式，若i∈PS，直接有fij＝nij，流程结束；若i∈PI，在L中搜索终点 D＝j且途经i站的径路，形成子集LOj＝{…}，LOj中的任意元素均满足i∈，如{Om,k1,k2,…,kr,i,…,j}，如图2所示。

图2 搜索过程示意图

步骤 3：中Om、i两站间的元素 (包括i站)k1,k2,…,kr，i即为车流解编备选站点，可据此生成各 OD 的解编接续备选方案，表述为决策变量的组合形式。其中i属于必经站，根据排列组合的方法枚举车流组织方案，利用决策变量联乘描述前后接续的车流改编链，如表1所示。在研究中发现，解编站点的搜索、选择过程遵循固定的规律，因此可在程序设计时将组合形式预置，依次套用即可。

表1 决策变量组合形式示例

4.3 目标规划法(GP)

目标规划法 (GP) 的核心思想是为每个目标函数设定一个标准值Fi，引入偏差变量和描述目标函数与标准值的近似程度，从而将原有的多目标函数转化为总偏差量最小的单目标函数，进而求得多目标模型的优化解。目标规划法的优势主要体现在以下两个方面。

（1）通过设定权重因子ωi来平衡和调整不同目标函数的数量级和优先级。

利用目标规划法 (GP) 将模型 (A) 转化为模型(B)：

模型 (B) 属于单目标 0-1 混合规划模型。在模型 (A) 中，目标函数Z1和Z2′均取最小值，因此在预设标准值时应保证F1

5 案例分析

以我国东北部分路网为例，对货物列车编组计划及编组站负荷分工进行联合优化。案例路网共包含 13 个技术站，其中沈阳西、山海关、四平和通辽为编组站，如图3所示。基础数据部分来源于有关项目：OD 共计 210 股，车流径路和技术站相关参数已知 (略)。共预设了4种不同的情形用于对比分析，使用 LINGO8.0 数学软件 (设置为全局最优解选项 ) 分别计算求解。

图3 案例路网结构示意图

情形①：不考虑编组站解编负荷状态最佳化的编组计划独立优化模型 (忽略模型 (A) 中的目标函数Z2或Z2′)。情形②：采用模型(B)，令＝0.8×＝2,4,12,14)，权重系数ω1＝ω2。情形

表2 LINGO 计算过程和结果的各项指标

表2中以 (i＝2,4,12,14) 表示i站的解编负荷量，β可解释为i站的负荷程度。情形①仅考虑列车编组计划的最优化，因此车流组织费用最低，然而沈阳西、四平、山海关3个编组站处于超负荷状态，通辽站的解编负荷量不足。情形②对货物列车编组计划和编组站负荷分工进行联合优化，沈阳西和通辽站的负荷状态明显好转，车流组织费用略有增加，但是四平和山海关站的负荷状态依旧不理想。情形③通过调整权重系数，使4个编组站的负荷均达到理想状态，但是车流组织费用显著增加。情形④的计算结果与情形③一致。通过分析可归纳得出以下结论。

（1）利用模型 (B )能够成功实现货物列车编组计划和编组站负荷分工的联合优化。

（2）目标规划法中权重系数的取值直接影响多目标模型的优化效果。在本案例中有nω1＝ω2，随着n值的增大，目标函数Z2或Z2′的优先性逐渐增强，Z1的优先性逐渐减弱，反之同理。这种优先性是存在极限的，如案例中情形③已达到极限效果，尽管情形④继续上调ω2的值，然而结果未发生变化。

（3）模型 (B) 中两个目标函数之间属于博弈关系，此消彼长，可以通过调整权重系数的方法进行均衡，但是最终方案需要人工决策。例如，案例中ω2的理论区间为 [ω1，2ω2]，其取值须根据试验效果和实际需求综合确定。

6 结束语

编组站解编负荷状态评价函数和曲线，构建了货物列车编组计划与编组站负荷分工联合优化模型 (A)，利用目标规划法 (GP) 转化为单目标模型(B)，并且设计了基于车流径路的fij搜索生成方法。案例结果表明，模型 (B) 实现了预期效果，对提高货物列车编组计划质量和优化编组站的分工布局具有重要的意义。在此过程中发现，参数Wibest与k超负荷与铁路现场的复杂因素有关，有待进一步研究和探索。

[1] 曹家明，朱松年. 铁路网上技术站直达列车编组计划优化的二次0-1规划法[J]. 铁道学报，1993，15(2)：62-69.

[2] 林柏梁，朱松年，赵 强. 技术直达列车编组计划的阶跃函数模型及同构变换[J]. 西南交通大学学报，1994，29(1)：91-96.

[3] 林柏梁. 机车长交路条件下的技术站列车编组计划无调作业参数模型[J]. 铁道学报，1999，21(6)：6-9.

[4] 许 红，马建军，龙 昭，等. 技术站单组列车编组方案模型与计算方法的研究[J]. 铁道学报，2006，28(3)：12-17.

[5] 林柏梁，徐忠义. 编组站布局规划模型[J]. 铁道学报，2002，24(3)：5-8.

[6] 曹学明，王喜富，林柏梁. 重空车流径路及多车种空车调配协同优化模型[J]. 中国铁道科学，2009，30(6)：114-118.

Optimization Model of Freight Car Marshalling Scheme and Load Dividing & Combining in Marshalling Station

GENG Ling-qian

(Freight Transportation, Shenyang Railway Administration, Shenyang 110001, Liaoning, China)

This paper puts forward the evaluation function and curve of uncoupling load status in marshalling station. With the target of minimum cost of train f ow organization and optimization of uncoupling load status in marshalling station, the optimization model of freight car marshalling plan and load dividing & combining in marshalling station is established, and the restriction condition, such as uniqueness of marshalling scheme, uncoupling capacity and shunting track number, were all considered. By using the GP method, the model was transferred from multi-goal into single goal, and corresponding search generating method was designed which programme had realized. In the end, based on the examples of actual railway network, the paper completes the model’s solution and contrastive analysis by using the LINGO mathematic software, and validates the rationality and validity of the model.

Railway; Marshalling Station; Marshalling Scheme; Optimization Model

1003-1421(2011)06-0059-05

U292.8；U291.4+12

A

2011-04-26

林 欣