2011年中考模拟测试题(1)

100048 首都师大附中 张文娣

2011年中考模拟测试题(1)

100048 首都师大附中 张文娣

一、填空题(每题3分，共30分)

1.－4的绝对值等于＿＿.

3.分解因式:ax2－8ax+16a=＿＿.

4.上海世博会是我国第一次举办的综合类世界博览会.据统计自2010年5月1日开幕至5月31日，累计参观人数约为8030000人.将8030000用科学记数法表示应为＿＿.

5.若一个正多边形的一个内角是144°，则这个多边形的边数为＿＿.

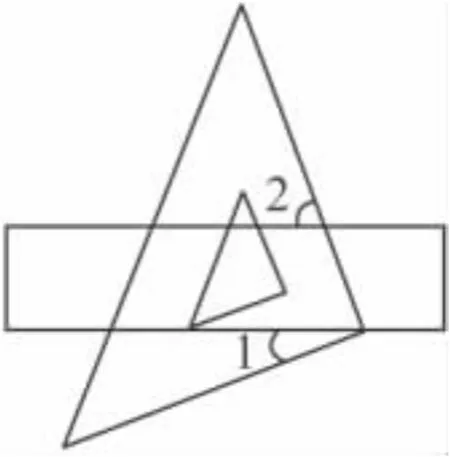
6.如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1 = 35°， 那 么 ∠2是＿°.

7.若⊙O的半径为5厘米，圆心O到弦AB的距离为3厘米，则弦长AB为 厘米.

8.已知2a2+a－1=0，则(a+2)2－3(a－1)+(a+2)·(a－2)的值为 .

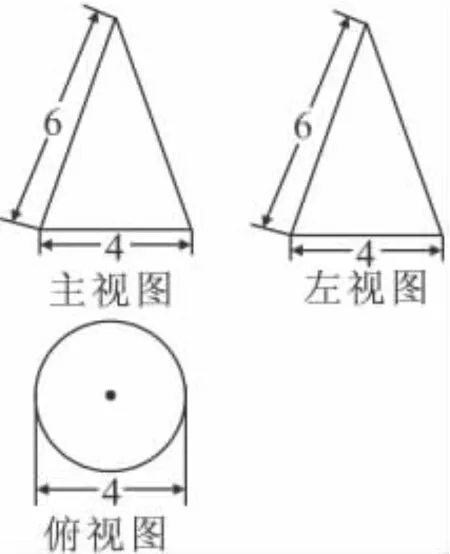
9.如图，是一个几何体的三视图，根据图中标注的数据可求得这个几何体的侧面积为.

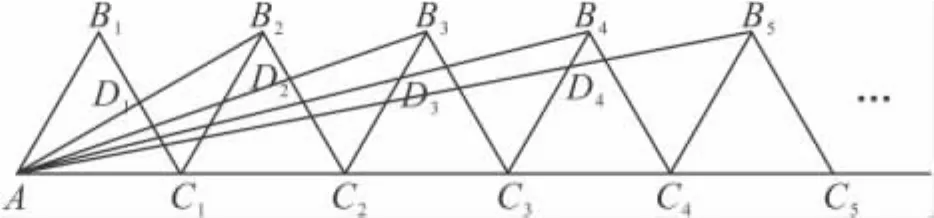
10.如图，n+1个边长为2的等边三角形有一条边在同一直线上，设△B2D1C1的面积为 S1，△B3D2C2的面积为 S2，…，△Bn+1DnCn的面积为 Sn，则 S2=＿

;Sn=＿ (用含n的式子表示).

二、选择题(每题3分，共18分)

11.下列计算正确的是 ( )

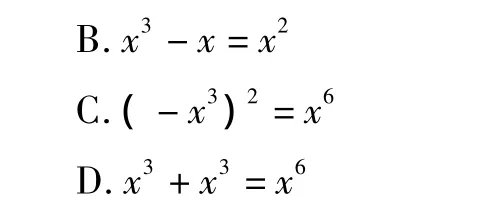
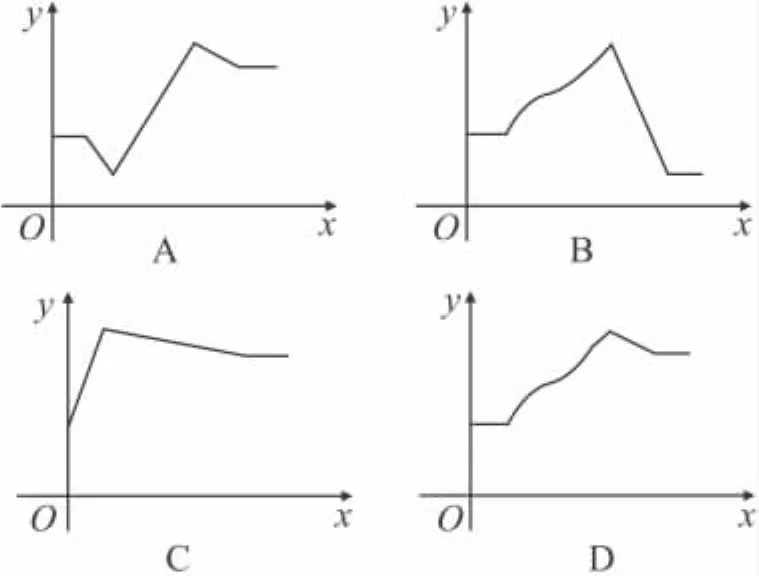
12.乌鸦口渴到处找水喝，它看到了一个装有水的瓶子，但水位较低，且瓶口又小，乌鸦喝不着水，沉思一会儿后，聪明的乌鸦衔来一个个小石子放入瓶中，水位上升后，乌鸦喝到了水.在这则乌鸦喝水的故事中，设从乌鸦看到瓶的那刻起向后的时间为x，瓶中水位的高度为y，下列图象中最符合故事情景的是()

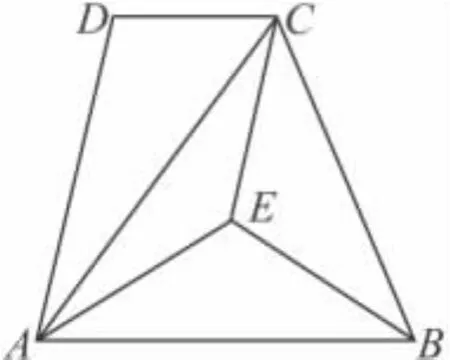
13.五箱救灾物资的质量(单位:千克)分别为:19，20，21，22，19，则这五箱救灾物资的质量的众数和中位数分别是 ( )

A.19，19 B.19，20

C.20，21 D.20，22

14.如图，AB是⊙O的直径，CD是弦，且 CD⊥AB，若 BC=6，AC=8，则sin∠ABD的值为()

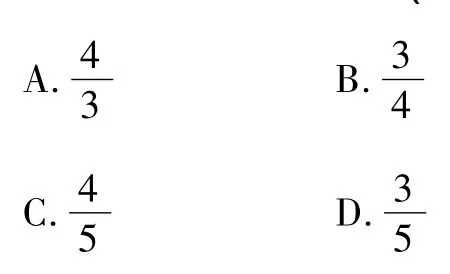
15.在平面直角坐标系中，对于平面内任一点P( a，b)若规定以下两种变换:

按照以上变换，那么f(g(a，b))等于 ( )

A.(－b，－ a) B.(a，b)

C.(b，a) D.(－ a，－ b)

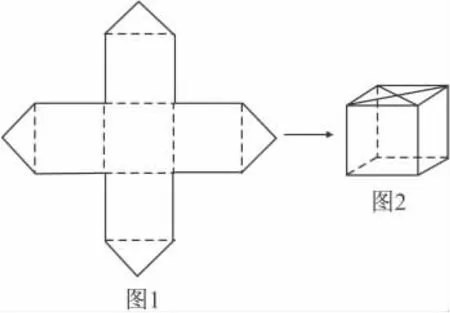
16.小明将一张正方形包装纸，剪成图1所示形状，用它包在一个棱长为10的正方体的表面(不考虑接缝)，如图2所示.小明所用正方形包装纸的边长至少为()

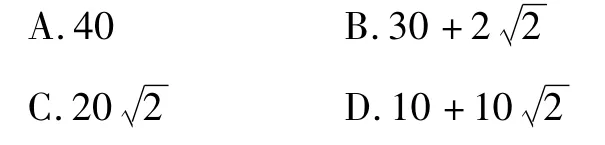
三、解答题(共9道题，共72分)

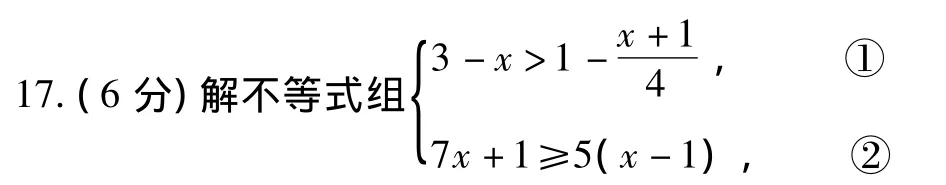
并把解集在数轴上表示出来.

18.(6分)如图，在四边形ABCD中，AC是∠DAE的平分线，DA∥CE，∠AEB=∠CEB.求证:AB=CB.

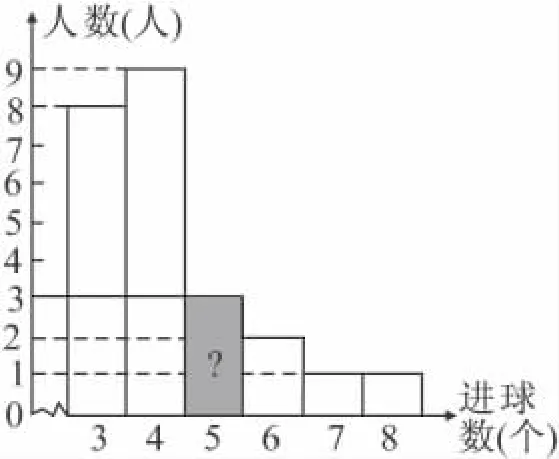
19.(6分)某班同学积极响应“阳光体育工程”的号召，利用课外活动时间积极参加体育锻炼，每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练，训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.

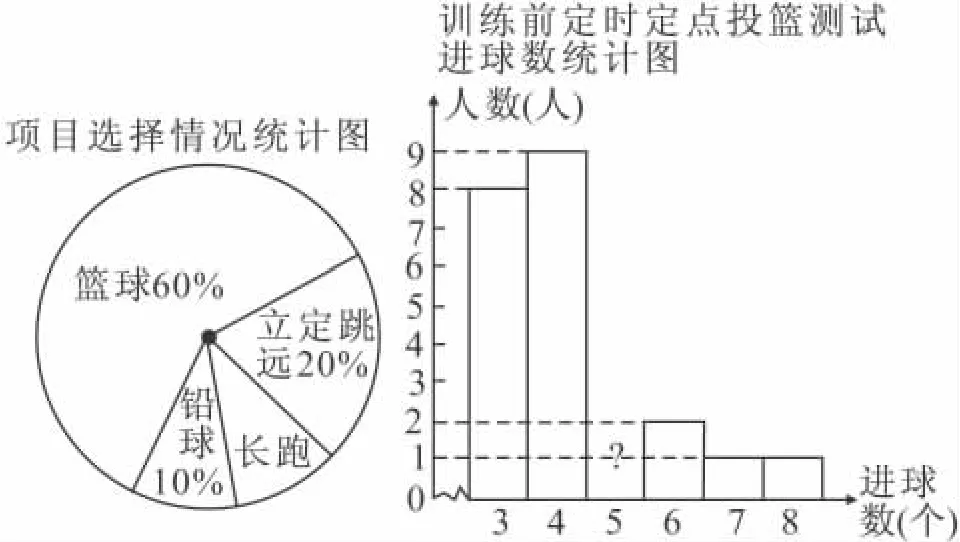
训练后篮球定时定点投篮测试进球数统计表:

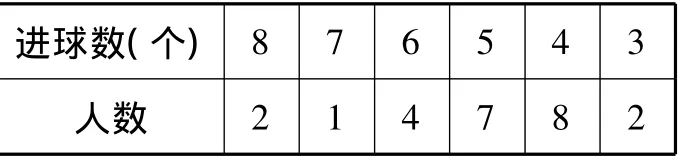
进球数(个)2 1 4 7 8 2 8 7 6 5 4 3人数

请你根据图表中的信息回答下列问题:

(1)选择长跑训练的人数占全班人数的百分比是＿，该班共有同学＿＿人;

(2)补全“训练前篮球定时定点投篮测试进球数统计图;

(3)训练后篮球定时定点投篮人均进球数

.

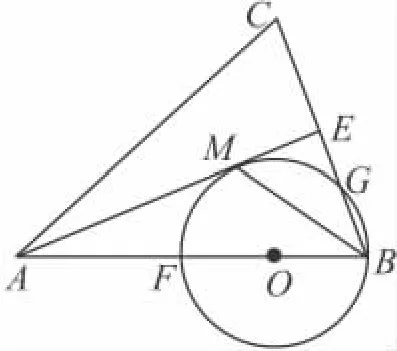
20.(7分)如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点 G，交 AB于点 F，

F

B恰为⊙O的直径.

(1)求证:AE与⊙O相切;

21.(8分)如图，在海面上有一股强台风，台风中心(记为点M)位于海滨城市(记作点A)的南偏西15°，距离为61千米，且位于临海市(记作点B)正西方向 60千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变)，距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.

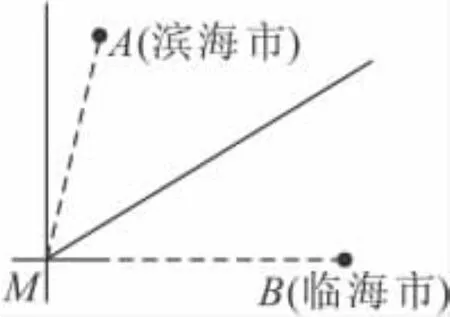
(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由;

(2)若受到此次台风侵袭，该城市受到台风侵袭的持续时间有多少小时?

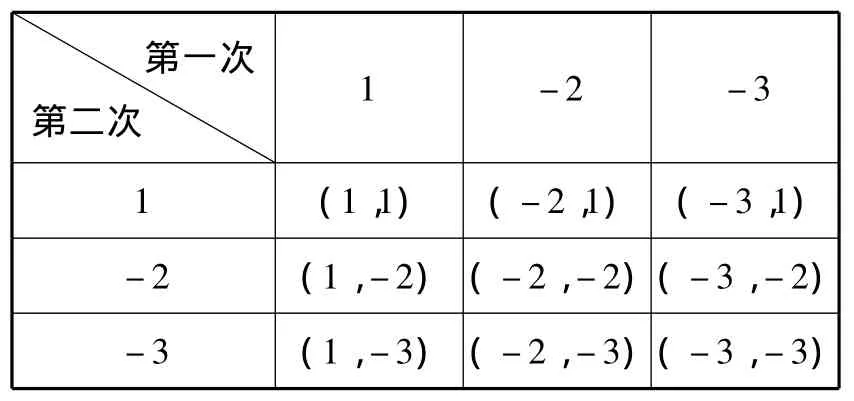
22.(6分)有三个完全相同的小球，上面分别标有数字1，－2，－3，将其放入一个不透明的盒子中摇匀，再从中随机摸球两次(第一次摸出球后放回摇匀)，设第一次摸到的球上所标的数字为m，第二次摸到的球上所标的数字为n，依次以m，n作为点M的横、纵坐标.

(1)用树状图(或列表法)表示出点M(m，n)的坐标所有可能的结果;

(2)求点M(m，n)在第三象限的概率.

23.(9分)某市在道路改造过程中，需要铺设一条长为1000米的管道，决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米，且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.

(1)甲、乙工程队每天各能铺设多少米?

(2)如果要求完成该项工程的工期不超过10天，那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.

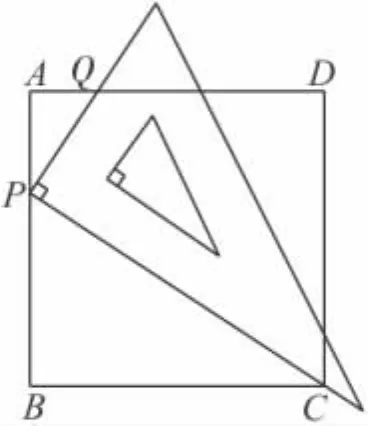
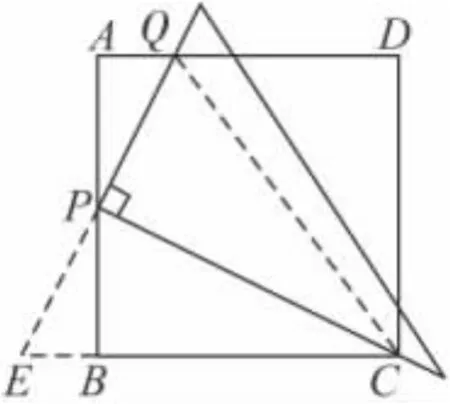
24.(12分)已知:如图，一块三角板的直角顶点P放在正方形ABCD的AB边上，并且使一条直角边经过点C，三角板的另一条直角边与AD交于点Q.

由于在电力、轨道交通与电动车辆等行业的生产、制造、物流及自动化过程中都需要大量的连接，包括物理连接和数字连接，而工业4.0、中国制造2025和互联网+进一步加速了这一进程，并通过数据分析、数据采集实现价值拓展，连接技术的未来发展方向将体现在电气化、自动化和数字化三大方面，这让浩亭如鱼得水，也正是浩亭连接技术解决方案要重点发展的领域。

(1)请你写出此时图形中成立的一个结论(任选一个);

(2)当点P满足什么条件时，有AQ+BC=CQ，请证明你的结论;

(3)当点Q在AD的什么位置时，可证得PC=3PQ，并写出过程.

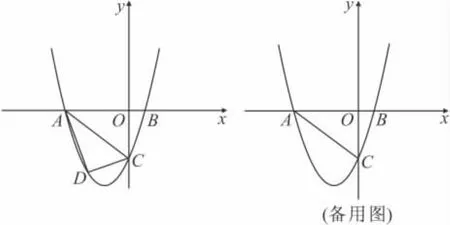
25.(12)如图，抛物线y=mx2+3mx－3(m＞0)与y轴交于点C，与x轴交于A，B两点，点A在点B的左侧，且tan∠OCB=.

(1)求此抛物线的解析式;

(2)如果点D是线段AC下方抛物线上的动点，设D点的横坐标为x，△ACD的面积为S，求S与x的关系式，并求当S最大时点D的坐标;

(3)若点E在x轴上，点P在抛物线上，是否存在以A，C，E，P为顶点的平行四边形?若存在求点P坐标;若不存在，请说明理由.

参考答案

一、选择题

1.4 2.－2 3.a(x －4)24.8.03 ×1065.10

二、选择题

11.C 12.D 13.B 14. C 15.A 16.C.

17.解不等式①x＜3，

解不等式②x≥－3，

原不等式组的解集为－3≤x＜3.

在数轴上表示为

18.∵AC是∠DAE的平分线，∴

∠1=∠2.

又∵ AD∥EC，∴ ∠2=∠3.

∴ ∠1=∠3.∴ AE=CE.

在△ABE和△CBE中，

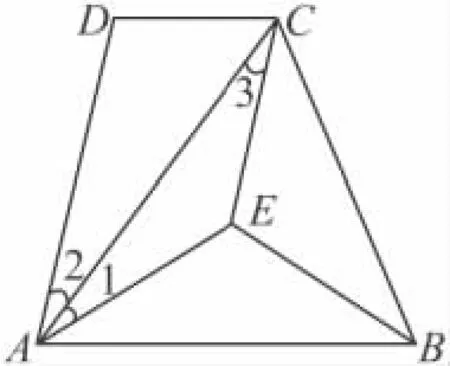
∴ △ABE≌△CBE.∴ AB=CB.

19.(1)10%;40;

(2)如图;

(3)5.

20.(1)连接 OM，则 OM=OB.

∴∠1=∠2.

∵BM平分∠ABC.

∴∠1=∠3.

∴∠2=∠3.

∴OM∥BC.

∴∠AMO=∠AEB.

在△ABC中，

∵AB=AC，

AE是角平分线，

∴ AE⊥BC.

∴ ∠AEB=90°.

∴ ∠AMO=90°.

∴OM⊥AE.

∴AE与⊙O相切.

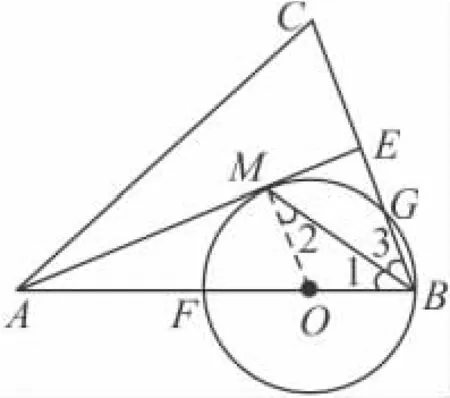
(2)在△ABC中，AB=AC，AE是角平分线，

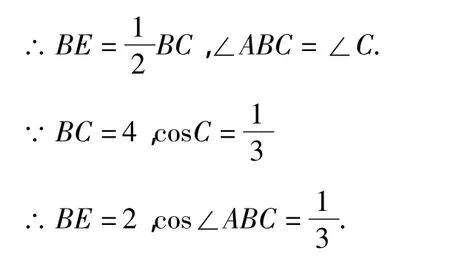
在△ABE 中，∠AEB=90°，

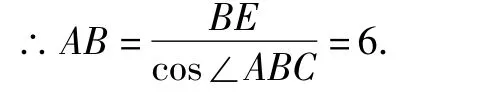
设⊙O的半径为r，则AO=6－r.

∵OM∥BC，

∴△AOM∽△ABE.

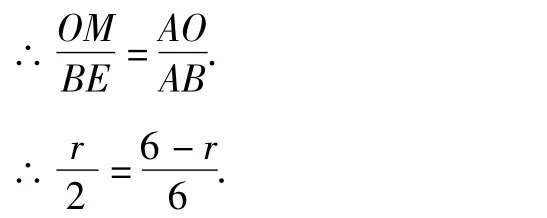
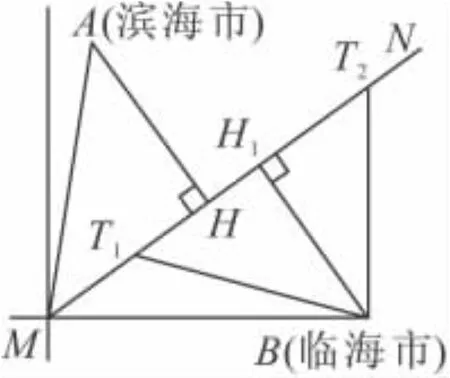
21.(1)设台风中心运行的路线

为射线MN，于是

∠AMN=60°－15°=45°，

过A作AH⊥MN于H，

故△AMH是等腰直角三角

形

∵AM =61■ 2，∴ AH=61＞60，

∴滨海市不会受到台风的影响;

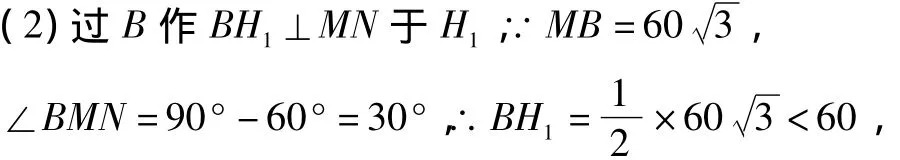
因此临海市会受到台风的影响;以B为圆心60为半径作圆与MN交于T1、T2，则BT1=BT2=60

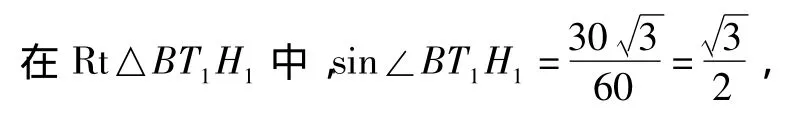
∴∠BT1H1=60°，∴△BT1T2是等边三角形，

∴T1T2=60，

22.(1)组成的点M(m，n)的坐标的所有可能性为

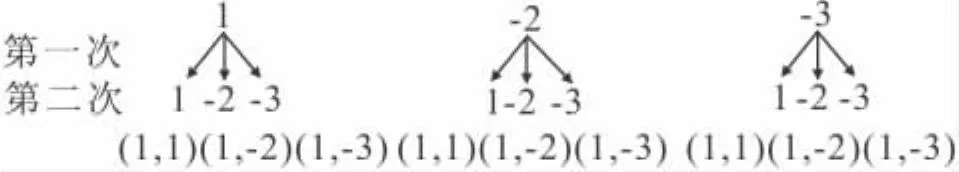
或列表如下:

?

(2)落在第三象限的点有(－2，－2)，(－2，－3)，(－3，－2)，(－3，－3)，因此点 M 落在第三象限的概率为.

23.(1)设甲工程队每天能铺设x米，则乙工程队每天能铺设(x－20)米.

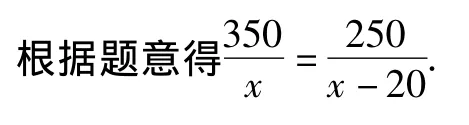
解得x=70.

检验:x=70是原分式方程的解.

答:甲、乙工程队每天分别能铺设70米和50米.

(2)设分配给甲工程队 y米，则分配给乙工程队(1000－y)米.

所以分配方案有3种.

方案一:分配给甲工程队500米，分配给乙工程队500米;

方案二:分配给甲工程队600米，分配给乙工程队400米;

方案三:分配给甲工程队700米，分配给乙工程队300米.

24.(1)△APQ∽△BCP.

(2)当P为AB中点时，有AQ+BC=CQ.

证明:连接CQ，延长QP交CB的延长线于点E.

可证△APQ≌△BPE，

则 AQ=BE，PQ=PE，

又因为 CP⊥QE，可得 CQ=CE，所以 AQ+BC=CQ.

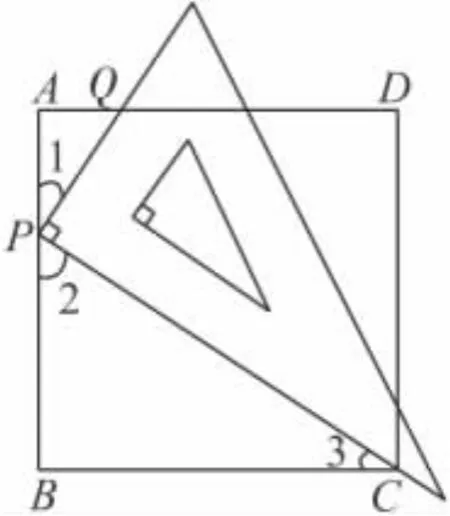
证明:在正方形ABCD中，∠A=∠B=90°，AD=BC=AB，又因为直角三角板的顶点P在边AB上，

所以 ∠1+∠2=180°－∠QPC=90°，

因为 Rt△CBP中，∠3+∠2=90°，

所以∠1=∠3.

所以△APQ∽△BCP，

∴ A(－4，0)，连接 OD，

∵点D在抛物线

图1

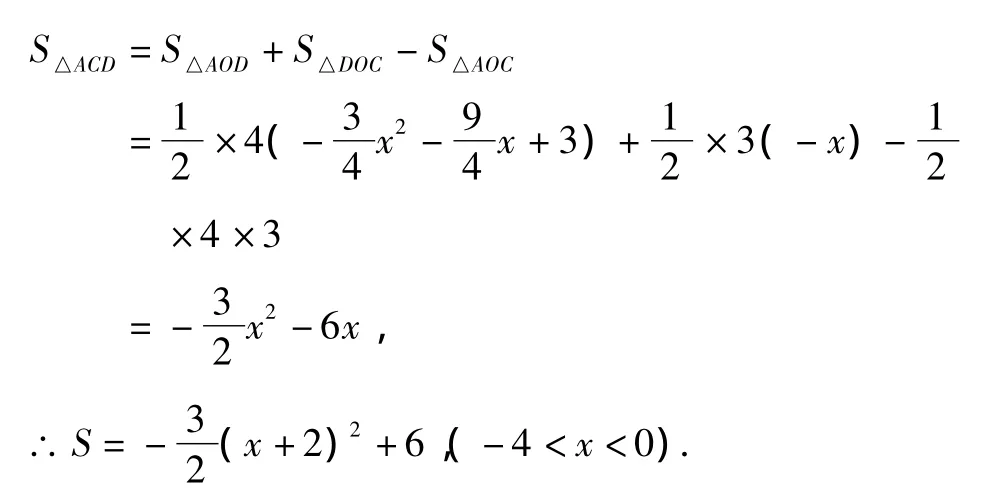
∴当x=－2时，△ACD的面积S有最大值为6.此时，点D的坐标为(－2，).

(3)①如图2，当以AC为边，CP也是平行四边形的边时，CP∥AE，点P与点C关于抛物线的对称轴对称，此时P(－3，－3);

②如图3，当以AC为对角线，CP为边时，此时P点的坐标是(－3，－3);

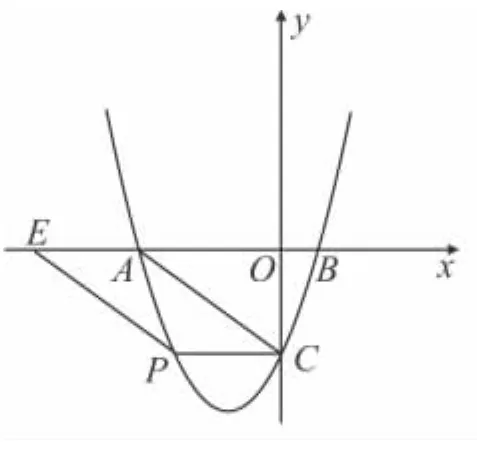
图2

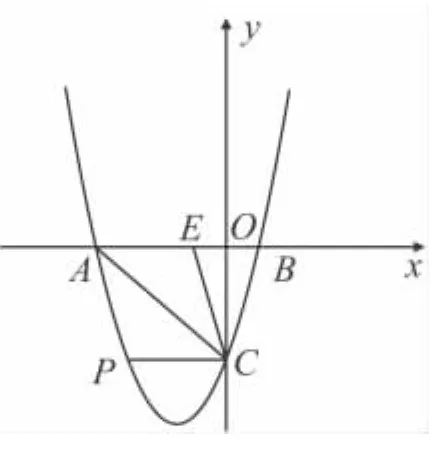
图3

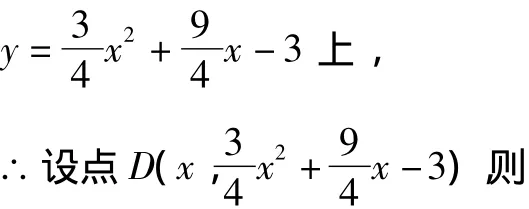
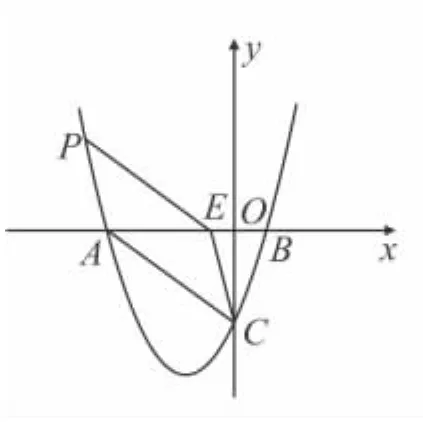
图4

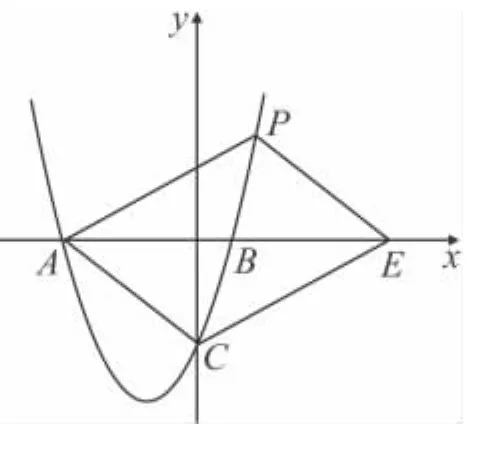
图5

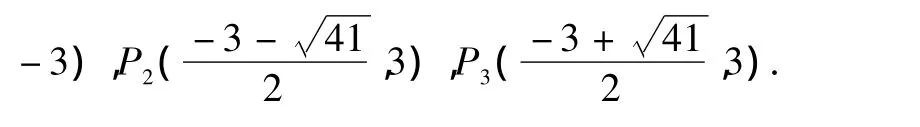
20110524)