主成分分析法与核主成分分析法在机械噪声数据降维中的应用比较

梁胜杰 张志华 崔立林

海军工程大学，武汉，430033

主成分分析法与核主成分分析法在机械噪声数据降维中的应用比较

梁胜杰 张志华 崔立林

海军工程大学，武汉，430033

依据线性降维与非线性降维的分类原则，分别选择主成分分析法和核主成分分析法对某双层圆柱壳体在不同工况下的机械噪声数据进行降维；然后使用神经网络和支持向量机两种方法分别计算噪声数据在降维前后的正确识别率，以比较不同降维方法的降维效果，从而确定适合于某双层圆柱壳体机械噪声数据的降维方法。

主成分分析法；核主成分分析法；核函数；神经网络；支持向量机；机械噪声；降维

0 引言

双层圆柱壳体的水下噪声主要来源于自身的机械设备［1］，此类噪声属于机械噪声。为了全面分析此类噪声的特点及规律，需要采用尽可能多的特征量进行表征。由于特征量很多，且特征量之间往往存在相关关系，因此很难直接抓住它们之间的主要关系，这就需要一种简化数据的方法使高维数据降维，以便获得噪声数据的主要信息。通过降维可以有效去除机械噪声数据中的冗余信息，从而降低数据分析处理的难度。

目前，数据降维方法主要分为两大类［2］：线性降维和非线性降维。主成分分析法（PCA）因为其概念简单、计算方便、线性重构误差最优等优良的特性，成为数据处理中应用最广泛的线性降维方法之一。核主成分分析法（KPCA）作为PCA方法在处理非线性问题时的扩展，近年来得到了快速发展。

本文将PCA方法和KPCA方法，应用于某双层圆柱壳体机械噪声数据的降维之中，然后使用神经网络（NN）和支持向量机（SVM）两种方法分别计算噪声数据降维前后的正确识别率，通过正确识别率比较PCA方法和KPCA方法的降维效果，从而选择更适合于这种双层圆柱壳体机械噪声数据的降维方法，并由此初步分析出噪声数据的线性或非线性特点。

1 PCA方法与KPCA方法的基本原理

PCA方法是一种基于二阶统计的数据分析方法，该方法在各个变量之间相关关系研究的基础上，用一组较少的、互不相关的新变量（即主元）代替原来较多的变量，而且使这些新变量尽可能多地保留原来复杂变量所反映的信息，具体计算步骤见文献［3］。

KPCA方法是一种非线性主元分析方法［4］。其主要思想是通过某种事先选择的非线性映射Φ将输入矢量X映射到一个高维线性特征空间F之中，然后在空间F中使用PCA方法计算主元成分。在高维线性特征空间中得到的线性主元实质上就是原始输入空间的非线性主元。

设xi∈Rd（i＝1，2，…，n）为输入空间的d维样本点。通过非线性映射Φ将Rd映射到特征空间F，即

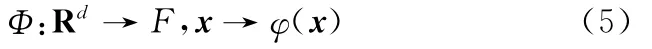
F中的样本点记作φ（xi）。

非线性映射Φ往往不容易求得，KPCA方法通过使用核函数来完成从输入空间到特征空间的非线性映射。定义核函数k（xi，xj）＝ 〈φ（xi），φ（xj）〉，这样特征空间中两向量的内积可以用输入空间中的两变量的核函数来表示。

核函数是满足Mercer条件的任意对称函数（实正定函数），常用核函数的特性如下：

其中，a、b、c、d、e、f 为选定的参数，通常取s（xi，xj）＝xTixj。

KPCA方法只需要在原空间中计算用作内积的核函数，无需知道非线性映射函数φ（x）的形式，也无需计算非线性变换，具体计算步骤见文献［5］。

PCA方法与KPCA方法已广泛应用于特征提取、数据压缩、图像降噪、分类识别、综合评价以及过程监视等诸多领域。

2 双层圆柱壳体机械噪声数据

在获取某双层圆柱壳体的机械噪声数据时，设定8个不同工况，如表1所示。

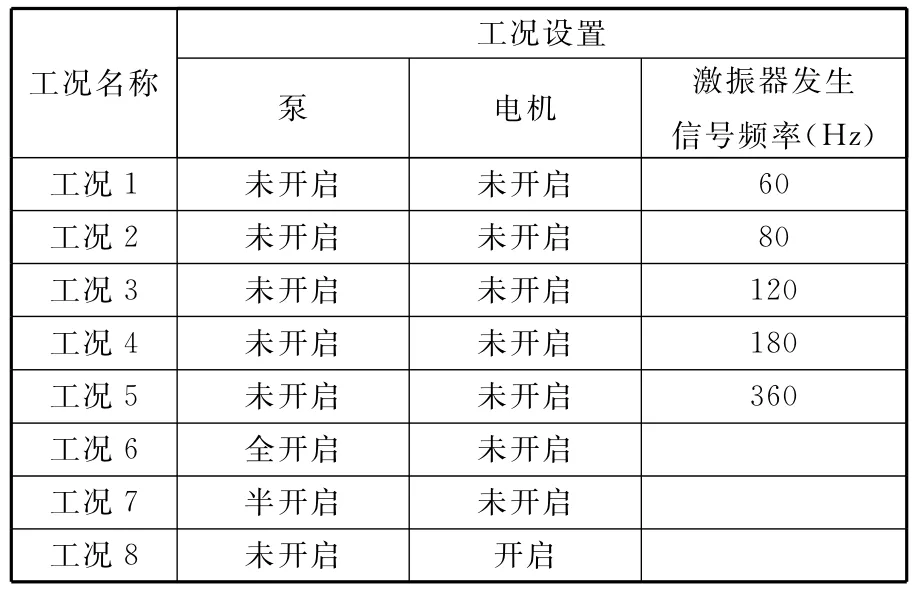
表1 工况设置

在壳体的不同位置布置19个加速度传感器（每个传感器称为一通道），测定不同工况下的噪声数据。采样时间为8s，采样频率为2048Hz。

由于在同一个通道下的采样点较多，且特征单一，不易分析其规律特点，因此对样本点进行预处理：

（1）选定信号处理中常用的10个特征量，即波形因数、峰值因数、脉冲因数、振动加速度总级、期望、方差、标准差、三阶累量、四阶累量和有效值。

（2）以2048个相邻样本点为一个样本段，并以70个样本点为步长，将样本段逐步向后平移，即可在16 384个样本点内得到约205个样本段。

（3）取前200个样本段，在每个样本段内计算选定的10个特征量。

本文重点是比较PCA方法与KPCA方法的降维效果，故只选取10个常用的特征量作为例子，实际上可以选择更多的特征量以更全面地表征噪声数据。

预处理后，在每一工况下的每一通道上可得到一个10×200（10是维数，200是样本量）的噪声数据，则在8种工况下，每一条通道上可得到8个10×200的噪声数据。

3 PCA方法与KPCA方法的主元数目

对上述噪声数据首先选择PCA方法降维，并依据累积贡献率大于0.85的门限值选择主元个数［3］。8种工况下，每一通道上噪声数据的PCA主元计算结果如表2所示。

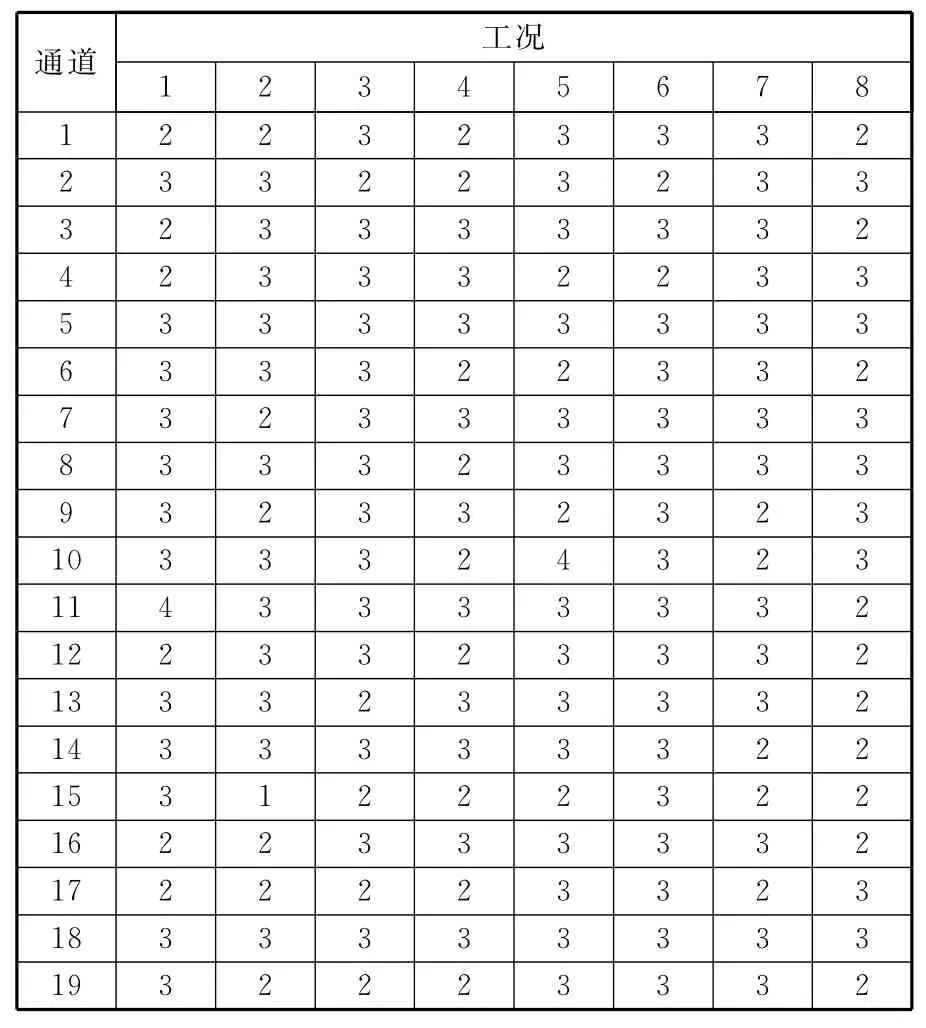
表2 PCA方法降维后的主元个数

由表2可知，8种工况下，在19条通道上的噪声数据经PCA方法降维后的主元个数为3的情况占67.1%，主元个数为2个的情况占30.9%，两种情况合计占98%。因此，为保证降维后的数据能够保留原始噪声数据足够多的信息，使用PCA方法降维时统一取3个主元。

本文主要比较PCA方法与KPCA方法对机械噪声的降维效果，因此使用KPCA方法时也取3个主元。

4 PCA方法与KPCA方法降维效果比较

4.1 比较方法

神经网络与支持向量机是模式识别领域最常用的两种方法。神经网络是一种基于经验风险最小原理的方法，它以分布式方式存储信息，具有高度的并行性、较强的自学习自适应性、良好的容错性和联想记忆功能，主要用于解决复杂的分类问题［6］。支持向量机是在 Vapnik［7］建立的统计学习理论基础上发展起来的机器学习算法，它主要基于VC维理论和结构风险最小化原理，能够很好地解决训练样本较少时的分类问题［8］。目前这两类方法已广泛应用于分类识别、故障诊断和入侵检测等领域之中［9－12］。

本文主要使用神经网络和支持向量机对不同工况下的噪声数据进行分类识别，通过对噪声数据的正确识别率，比较PCA和KPCA两种方法降维效果的好坏。

某双层圆柱壳体机械噪声数据经过降维后，若保留原始信息越多，则来自不同工况下的组合数据经过NN或SVM分类后的正确识别率就会越高；反之，正确识别率就会越低。在每一通道下，使用NN和SVM计算噪声数据降维前和分别经PCA方法、KPCA方法降维后的正确识别率。依据正确识别率比较两种降维方法的降维效果，同时也比较KPCA方法在选择不同核函数时的降维效果。降维后，X′i和X″i分别为3×k的数据和3×l的数据。

本文使用的神经网络为BP神经网络，支持向量机工具箱为stprtool，训练样本个数和测试样本个数取k＝l＝5，运行平台均为MATLAB7.1。

4.2 KPCA方法在不同核函数时的降维效果比较

KPCA方法是基于核函数的学习方法。核函数反映了样本在高维特征空间中彼此的相似程度，而样本之间的相似程度一旦给定，样本间的分类其实也就基本上确定了。一个好的核函数，会使同类的样本相互靠近，使异类的样本相互远离。正确选择核函数和核参数将会提高KPCA方法的整体性能。

计算可知，对于文中的噪声数据使用KPCA方法降维时，选择Sigmoid核函数得到的s（xi，xj）较大，此时k（xi，xj）总趋向于1。因此，本文只选取高斯径向核函数和多项式核函数进行计算，且b＝c＝1，a与d根据经验在一定范围内取值。

根据经验，使用高斯径向核函数（称为KP－1方法）和多项式核函数（称为KP－2方法）时，选择核参数a、d的取值范围为0.1～1，步长为0.1。经MATLAB编程计算，其结果如表3所示。

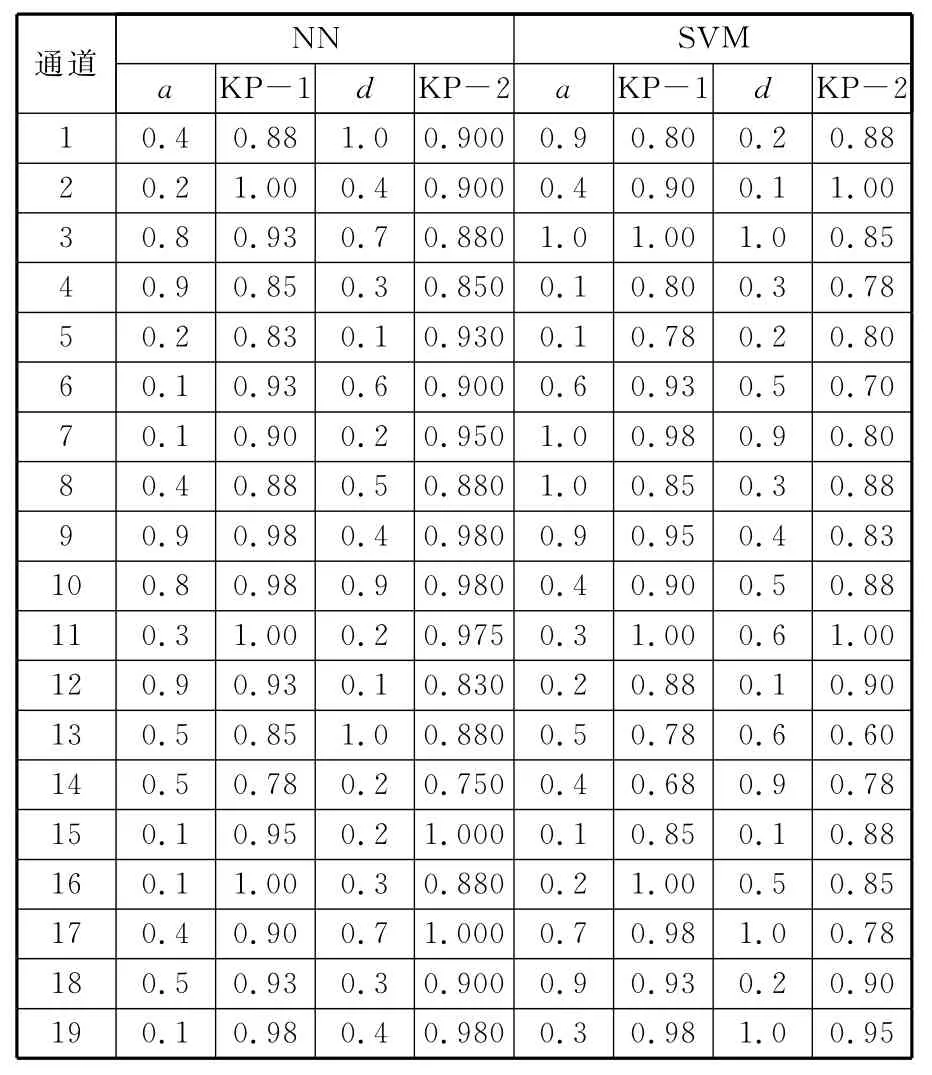
表3 KP－1方法与KP－2方法降维后的正确识别率

表3中，第3、5、7、9列分别是KP－1方法与KP－2方法在各自核参数取值范围内得到的正确识别率最大值，此时a与d分别为对应的核参数值。可以看出：使用神经网络进行分类识别时，KP－1方法正确识别率高于KP－2方法正确识别率的有8条通道，小于KP－2方法正确识别率的有6条通道，两者相当的有5条通道，即KP－1方法的降维效果稍好；使用支持向量机进行分类识别时，KP－1方法正确识别率高于KP－2方法正确识别率的有11条通道，小于KP－2方法正确识别率的有7条通道，两者相当的有1条通道，即KP－1方法的降维效果明显较好。

两种识别方法在19条通道上的运行总时间和单通道上运行的平均时间如表4所示。

表4 NN与SVM进行分类识别的运行时间 s

由表3中的正确识别率和表4中的运行时间可知，同等条件下神经网络方法和支持向量机方法在识别能力方面差别不大，但是支持向量机方法的运算速度要快得多。因此对于某双层圆柱壳体的机械噪声数据，在使用KPCA方法进行降维处理时，最好选择高斯径向核函数，并通过支持向量机方法进行分类识别分析。

4.3 PCA与KPCA方法的降维效果比较

对8个不同工况下的机械噪声数据组成的混合数据分别使用NN和SVM计算降维前后的正确识别率，其结果如表5所示。

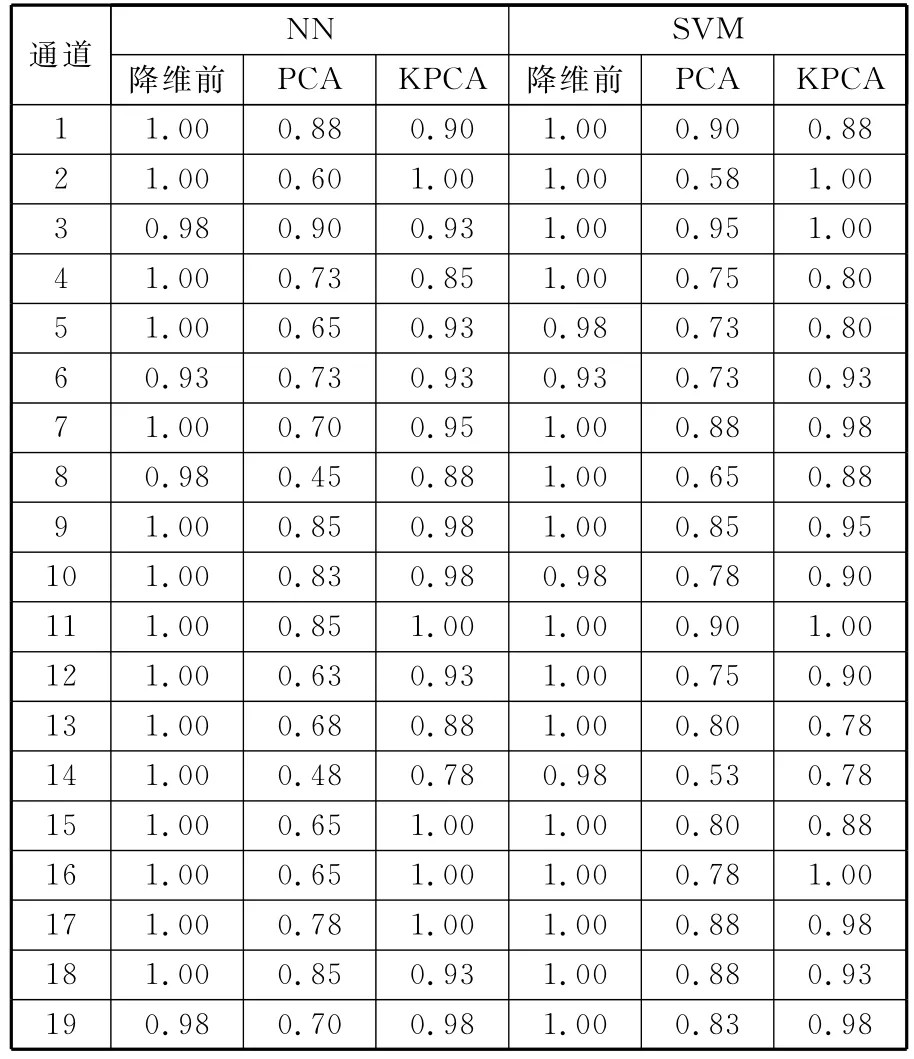
表5 机械噪声数据降维前后的正确识别率

比较表5中计算结果可知，不论使用哪种识别方法，降维前的正确识别率都比降维后的正确识别率高（至少相等），而由KPCA方法降维后得到的正确识别率在绝大部分通道上要比PCA方法降维后的正确识别率高。也就是说，数据降维后会损失掉一部分原始信息，造成正确识别率下降，但是对于某双层圆柱壳体的机械噪声数据来说，在主元数目相同的条件下，只要选择合适的核函数及核参数，就能保证使用KPCA方法降维后保留的信息要比使用PCA方法降维后保留的信息要多，即KPCA方法的降维效果要好。

5 结束语

事实上，可将本文中的10个特征量扩展到几百个甚至上千个，此时的噪声数据属于典型的高维数据，分析其结构前先进行降维就显得十分必要。通过本文对PCA方法和KPCA方法实际应用的比较可知：在主元数目相同（即数据结构的复杂度相同）的条件下，由于将数据特点的研究范围从线性扩大到非线性上，从而使得使用KPCA方法降维比使用PCA方法降维保留的原始数据信息更多，效果更好，因此，对某双层圆柱壳体机械噪声数据降维时，应优先考虑使用非线性降维方法——KPCA方法，且选择高斯径向核函数效果更好。

［1］ 施引，朱石坚，何琳.舰船动力机械噪声及其控制［M］.北京：国防工业出版社，1990.

［2］ 吴玲达，贺玲，蔡益朝.高维索引机制中的降维方法综述［J］.计算机应用研究，2006，23（12）：4－7.

［3］ Jolliffe I T.Principal Component Analysis［M］.2nd ed.New York：Springer，2002.

［4］ Scholkopf B，Smola A，Muller K R.Nonlinear Component Analysis as a Kernel Eigenvalue Problem［J］.Neural Computation，1998，10（5）：1299－1319.

［5］ Rosipal R，Girolami M，Trejo L J，et al.Kernel PCA for Feature Extraction and De－noising in Non－linear Regression［J］.Neural Computing and Applications，2001，10（3）：231－243.

［6］ 王洪远，史国栋.人工神经网络技术及其应用［M］.北京：中国石化出版社，2002.

［7］ Vapnik V N.The Nature of Statistical Learning Theory［M］.New York：Springer－Verlag，1995.

［8］ Vapnik V N.Statistical Learning Theory［M］.New York：Wiley，1998.

［9］ Suykens J A K，Vandewalle J.Least Squares Support Vector Machine Classifiers［J］.Neural Processing Letters，1999，9（3）：293－300.

［10］ Wu J N，Wang J，Liu L.Feature Extraction via KPCA for Classification of Gait Patterns［J］.Human Movement Science，2007，26（3）：393－411.

［11］ 高海华，杨辉华，王行愚.基于PCA和KPCA特征抽取的SVM网络入侵检测方法［J］.华东理工大学学报（自然科学版），2006，32（3）：321－326.

［12］ 鲁书贤，刘正熙，刘显宾，等.基于SVM和NN的空管手写符号的识别研究［J］.四川大学学报（自然科学版），2008，45（4）：790－794.

Comparison between PCA and KPCA Method in Dimensional Reduction of Mechanical Noise Data

Liang Shengjie Zhang Zhihua Cui Lilin
Naval University of Engineering，Wuhan，430033

According to the classification principle of linear and non－linear dimensional reduction，this paper dealt with mechanical noise data under different working－modes through PCA and KPCA.Lastly，the paper computed the right recognition percentage of noise data，including had been reduced and not，by NN method and SVM method，and compared the excellence for PCA and KPCA in dimensional reduction.Consequently，a better method of dimensional reduction is selected for ribbed cylindrical double－shells according to the results.

PCA（principal components analysis）；KPCA（kernel PCA）；kernel function；NN（neural network）；SVM（support vector machine）；mechanical noise；dimensional reduction

TB53；O212.4

1004—132X（2011）01—0080—04

2010—01—15

国家自然科学基金资助项目（50775218）

（编辑 郭 伟）

梁胜杰，男，1981年生。海军工程大学兵器工程系博士研究生。主要研究方向为武器系统总体技术、高维数据处理。张志华，男，1965年生。海军工程大学应用数学系教授、博士研究生导师。崔立林，男，1981年生。海军工程大学振动与噪声研究所博士研究生。