基于正交补的6-3 Stewart并联机构运动学正解
程世利 吴洪涛 王超群,2 姚 裕 朱剑英
1.南京航空航天大学,南京,210016 2.南京农业大学,南京,210031
基于正交补的6-3 Stewart并联机构运动学正解
程世利1吴洪涛1王超群1,2姚 裕1朱剑英1
1.南京航空航天大学,南京,210016 2.南京农业大学,南京,210031
提出了一种研究6-3 Stewart并联机构运动学正解问题的新方法。通过分析动平台位姿变量之间的耦合关系,增加了一些有用的信息,得到了用于解决这一问题的11个相容方程。使用正交补方法进行消元,最终可以将6-3 Stewart并联机构运动学正解问题表达成一个一元八次方程。最后通过一个实例验证了该方法的正确性。
Stewart平台;并联机构;运动正解;正交补;解析法
0 引言
6-3 Stewart并联机构是6-6 Stewart并联机构的一种典型特例,其动平台铰链点的连线是一个三角形,静平台铰链点的连线仍然是六边形[1]。所谓的运动学正解问题就是已知驱动杆的杆长,求解动平台相对于静平台的位置与姿态变量。
多年以来,这类机构的运动学正解问题引起了众多学者的广泛关注。文献[1-2]提出了一种解析化方法,将这类并联机构的运动学正解问题表达为一个一元十六次的代数方程。文献[3-4]也将这一问题表达成一个一元十六次的代数方程,但是方法过于复杂。文献[5]利用四面体原理研究这一问题,提出一种封闭解法,但是正解方程不是位姿变量的显式表达形式。很多学者试图运用数值方法解决这一问题,也取得了一些进展[6-8]。
本文在文献[2,9]的基础上,通过分析动平台位姿变量之间的耦合关系,增加有用的信息,得到了用于解决这一问题的11个相容方程。在此基础上,反复使用正交补方法进行消元,逐步降低变量的次数,最终可以将6-3 Stewart并联机构运动学正解问题表达为一个一元八次方程。本文所提出的方法对于所有的动静平台顶点平面布置的6-3 Stewart并联机构都是适用的。
1 基本方程及线性消元
为了问题研究的方便,动静坐标系的坐标原点设置如图1所示,其中Z′轴与Z轴分别垂直于动静平台平面。动平台的顶点坐标在动坐标系中可以表示为
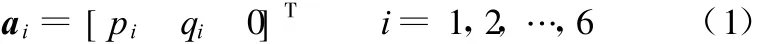
由于动平台是三角形的,故顶点1与顶点2重合,顶点3与顶点4重合,顶点5与顶点6重合。静平台顶点坐标在静坐标系可以表示为

动静坐标系之间的旋转矩阵R采用方向余弦矩阵描述:
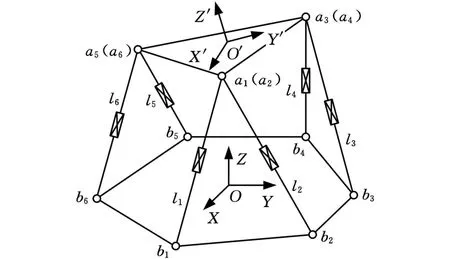
图1 6-3 Stewart并联机构示意图
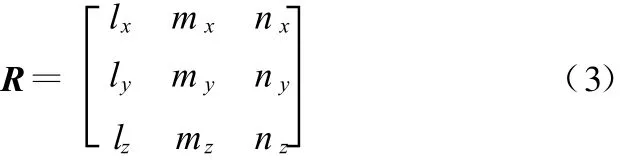
旋转矩阵共有9个元素,但是只有3个是独立的,其他6个元素存在如下3个约束条件:
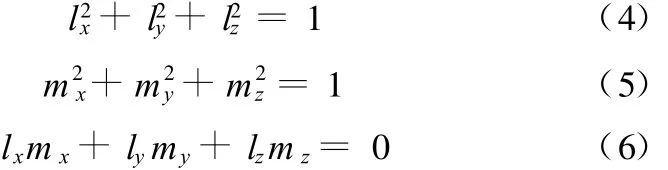
动坐标系的原点在静坐标系中的坐标用矢量P=[x y z]T描述,则各杆的杆长就可以表示为
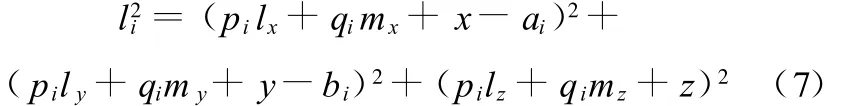
由于动静平台均为平面布置,故式(7)中不含nx、ny、nz。这样运动学正解只需要求解 9个未知数即可。为了研究方便,在以下分析过程中引入两个中间变量w1和w2。
位置矢量P=[x y z]T的模,即矢量长度的平方为
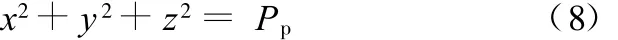
根据式(8)、旋转矩阵的正交以及归一化特性进行化简之后,有
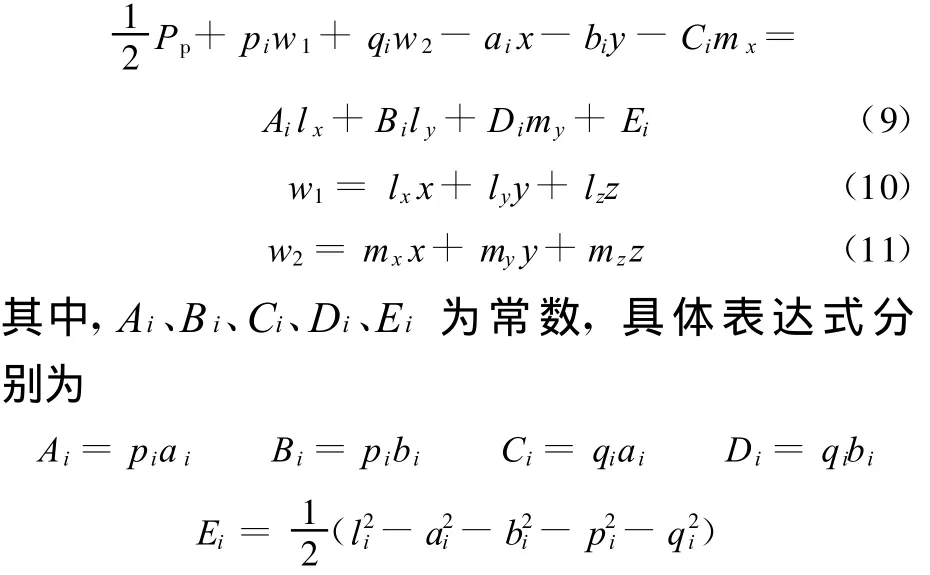
式(9)为由6个含有9个未知数的代数方程组成的方程组。选择其中的 3个未知数 lx、ly、my作为基本变量 ,则其余的 6 个未知数 P p、w1、w2、x 、y和mx就可以用这3个基本变量来线性表示:
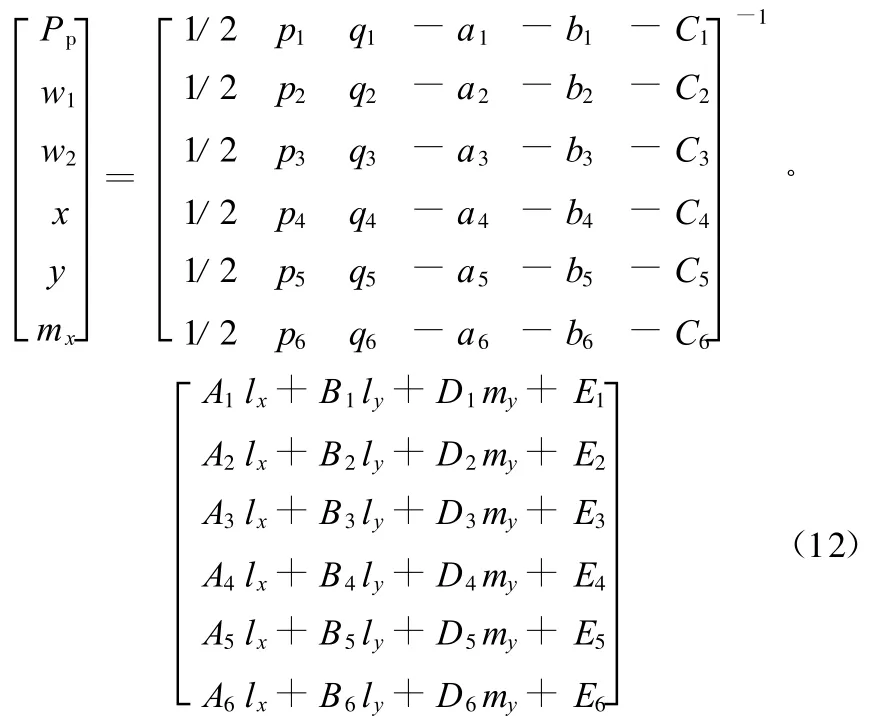
由式(12)就可以解得 P p、w1、w2、x、y 和m x关于lx、ly、my的表达式。
2 位置姿态变量的耦合关系
2.1 位姿变量的耦合关系
根据旋转矩阵的正交性、归一性,从式(4)~(6)、式(8)知,3个未知数 z、lz、mz有如下关系:
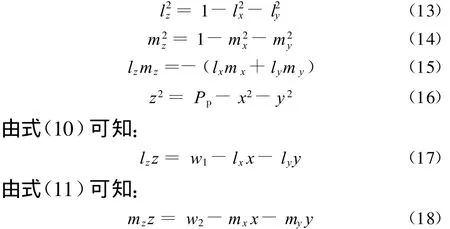
将式(13)~式(18)代入到如下6个恒等式中就可以得到只含有变量 lx、ly、my的方程组:
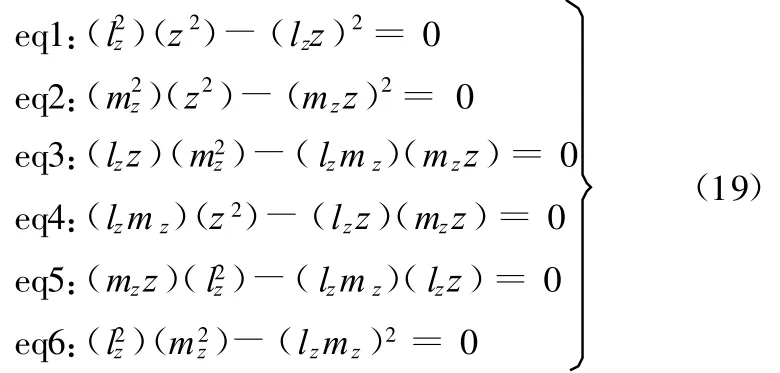
Zhang等[9]在他们的著作中提出了这6个恒等式。研究发现,在此基础上还有另外一些信息是可以利用的,同时这对于运动学正解问题的研究是有帮助的,下面将对这一点进行阐述分析。
2.2 耦合关系的附加方程
动平台位置矢量在静坐标系中用P表示,在动坐标系中用W表示,它们之间有如下关系:

经过研究可以发现,w1、w2的物理意义就是矢量W的前两个分量。由式(20)可以得到一组对应关系:
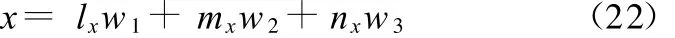
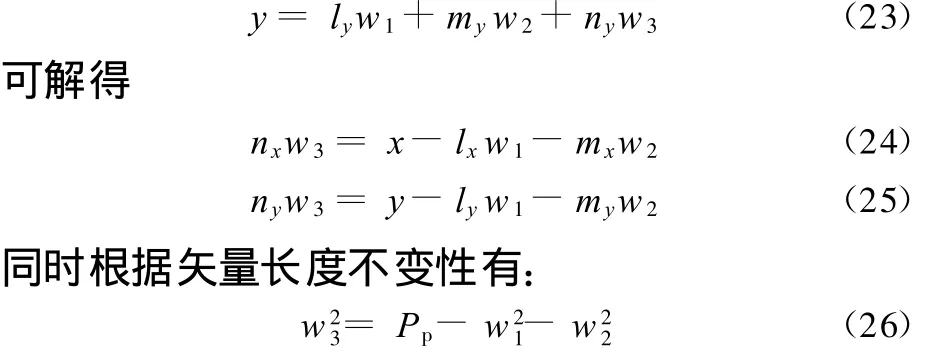
根据旋转矩阵的正交性、归一性,可以得到如下3个关系:
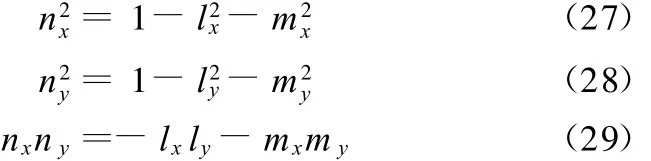
利用式(24)~式(29),就有以下6个等的式存在:

eq6和eq12展开后完全一样,所以应舍去一个,在此舍去 eq12。增加的 5个方程对解决Stewart型并联机构的运动学正解问题是有帮助的,这一点可以在后面的分析中得到验证。
3 正交补消元过程
3.1 正交补消元
将eq1~eq11这11个方程中的my作为保留变量,消去ly和lx,最后得到关于my的代数方程。具体的方法是用1、ly、lx分别乘以eq1 ~eq11,就可以得到33个方程式。
为了利用正交补进行消元,将ly和lx的不同组合进行如下排列:
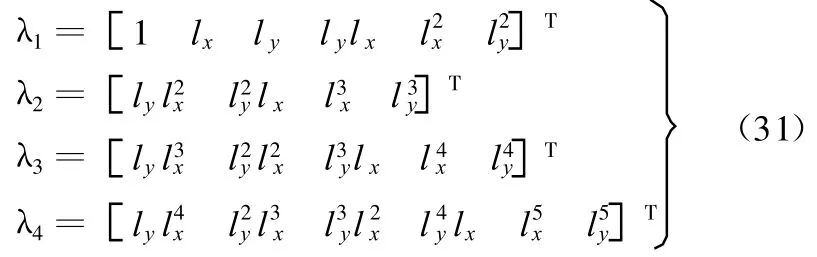
将所得到33个方程简写为
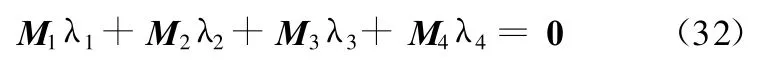
其中,M 1在理论上是my的4次多项式,但是对于6-3 Stew art并联机构,4次项可能不出现;M2、M3是m y的2次多项式和1次多项式;M 4是常数项。如果把系数矩阵M 1、M2 、M 3 、M 4按my的幂展开,式(32)就有:
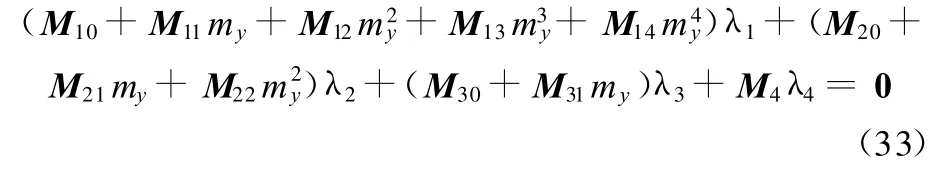
通过利用正交补的方法消去 λ4、λ3、λ2、m3yλ1以及 m4yλ1就可以得到一个关于 λ1的线性方程组:
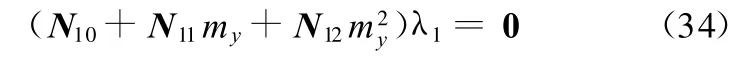
式中,N12为m2y的系数组成的矩阵;N11为my的系数组成的矩阵;N10为常数项组成的矩阵。
将(N10+N11my+N12m2y)记为 Ms(Ms∈R11×6),其阶数随着具体问题的不同而有所变化。任取Ms的6行组成一个方阵,记为M,因为方程组有非零解,所以其行列式为零,即

由于M s的行数大于列数,所以可以解得多个一元高次的代数方程。这些代数方程的次数可能是高于8的,但是次数高于8次的项系数是非常小的,大多数情况下可以把这些项直接舍去。为了求解的精确性,可以多取几个这样的方程,将这些高于8次的项解出来代入到剩余的方程中,就可以得到所需要的一元八次方程。
3.2 其他分量的求解
在解得my之后,lx、ly就可以由式(34)唯一确定 ;P p、w1、w2、x、y、mx 可以由式(12)中的相应关系式解得;z、lz、mz则分别由下列3个式子求得:
最后剩余的三个变量nx、ny、nz则分别由下列3个式子求得:
由以上分析可以看出,共有16种位形与一组杆长条件对应。
4 算例
本节通过一个计算实例来验证本文方法的正确性。动静平台的顶点坐标如表1所示。由于动静平台的顶点均为平面布置,所以Z分量均为零。
预先给出一组反解。其旋转矩阵为
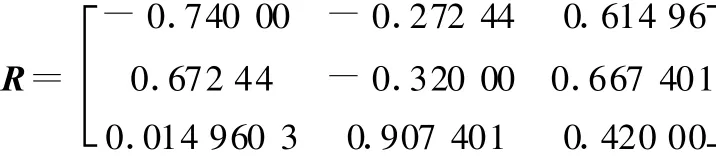
位置矢量P=[2 3 15]T。经过反解计算得到对应的杆长:l1=16.3313,l2=14.3936,l3=15.0360,l4=14.2424,l5=17.7981,l6=18.4852。
应用本文提出的方法进行运动学正解的求解,可以得到多个一元八次代数方程。图2中给出了其中的8个一元八次方程所对应的线条曲线。其中一个曲线所对应的方程为
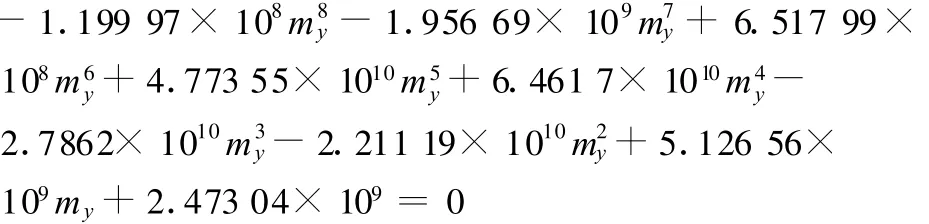
这些一元高次方程都是同解的,它们的解均为
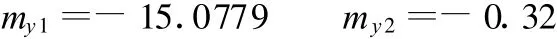
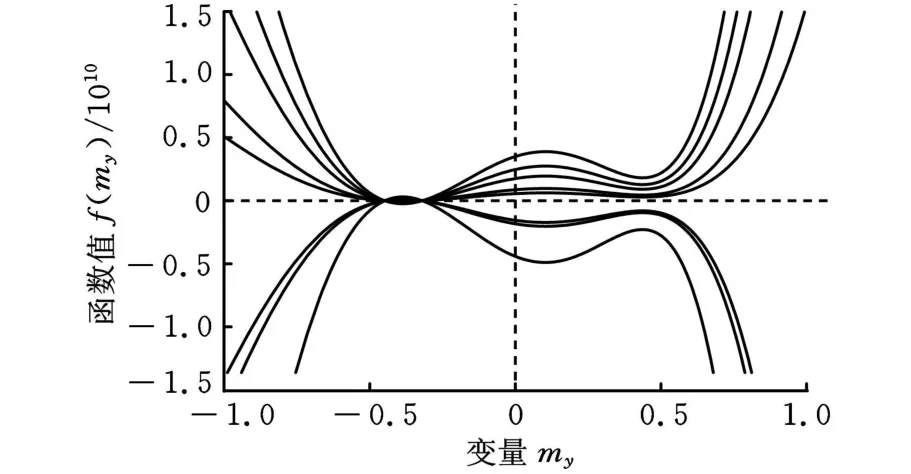
图2 关于my正解方程的曲线
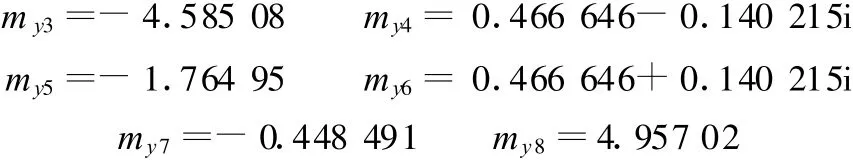
可见它们在[-1,1]之间有两个共同的零点。它们共同的实数根是:-0.32和-0.448 491,其中-0.32是开始设置的结果。其他位置和姿态变量的计算结果如表2所示。经过计算发现,所有的16组位形都满足杆长约束,从而反映了所提出的方法和计算的结果是完全正确的。
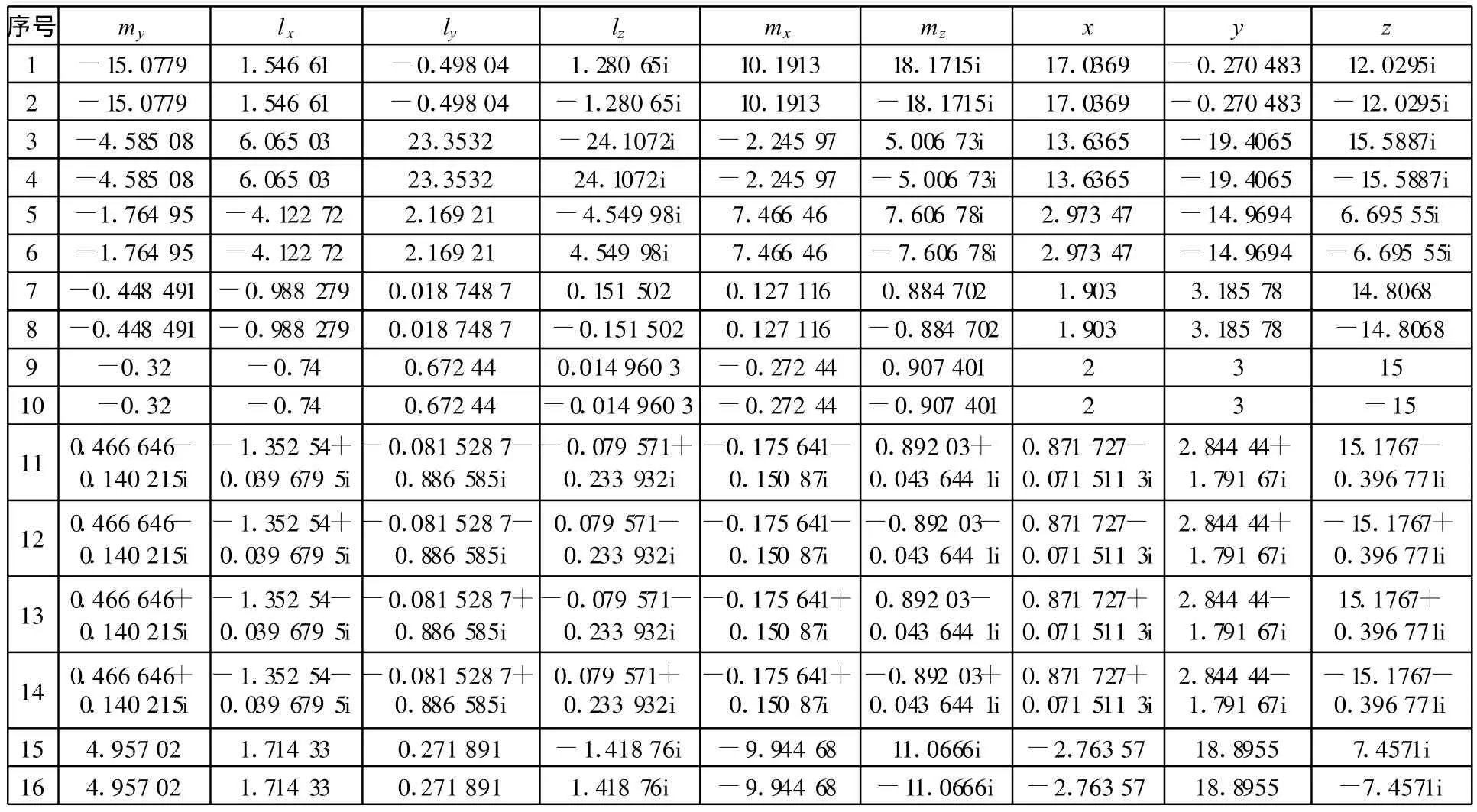
表2 计算实例的全部正解
5 结语
在前人研究成果的基础上,结合独立研究的成果对6-3 Stew art并联机构的运动学正解问题进行了研究。充分利用旋转矩阵的正交性、归一性,增加了有用信息,即增加了5个相容方程;运用正交补的方法进行消元,可得到若干个一元八次方程。
本文的方法对于所有类型的6-3 Stewart并联机构都是适用的。本文方法的另一个优点是最终的一元高次方程是关于位姿变量的函数,这是一种显式表达,不需要再进行转换处理。将此类问题的运动学正解表达为一元八次代数方程,相比于以前表示为16次的代数方程,是一个突破。这不仅有助于此类机构运动学的研究,还将推动此类机构工作空间等基本问题的研究。
[1] 黄真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.
[2] 黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.
[3] Nanua P,Wald ron K J,Murthy V.Direct K inematic Solution of a Stew art Platform[J].IEEE Transactions on Robotics and Automation,1990,6(4):438-444.
[4] Akçali I D,Mutlu H.A Novel Approach in the Direct Kinematics of Stew art Platform Mechanisms with Planar Platforms[J].ASME Journal of Mechanical Design,2006,128(1):252-263.
[5] Song SK,Kw on DS.New Closed-form Direct K inematic Solutionof the3-6 Stewart-gough Platform U-sing the Tetrahed ron Approach[C]//Proceedings of the International Conference on Control,Automation and Systems.Jeju,Korea,2001:484-487.
[6] Yurt S N,An li E,Ozkol I.Forw ard Kinematics Analysis of the 6-3 SPM by Using Neural Networks[J].M eccanica,2009,42(2):187-196.
[7] Ku DM.Forw ard Kinematic Analysis of a6–3 Type Stewart Platform Mechanism[J].Proceedings of the Institution ofMechanical Engineers,Part K:Journal of M ulti-body Dynam ics,2000,214(4):233-241.
[8] Yee C S,Lim K B.Forward Kinematics Solution of Stewart Platform Using Neural Networks[J].Neurocomputing,1997,16(4):333-349.
[9] Zhang C D,Song SM.Forw ard Position Analysis of Nearly General Stewart Platforms[J].ASME Journal of Mechanical Design,1994,116(1):54-60.
Forward Kinematics Analysisof 6-3 Stewart Parallel Mechanisms Based on Orthogonal Comp lement Method
Cheng Shili1Wu H ongtao1Wang Chaoqun1,2Yao Yu1Zhu Jianying1
1.Nan jing University of Aeronautics&Astronautics,Nan jing,210016
2.Nanjing Agricultural University,Nanjing,210031
This paper presented a new analyticalm ethod to study the forward kinematics analysis of 6-3 Stewart parallelmechanism s.Analyzing the coup ling relationships among the position and orientation variables of the moving p latform,additionaluseful information was obtained,thus eleven com patible algebra equations used to solve this p roblem were obtained.The orthogonal comp lem ent method was used to eliminate the redundant variab les,the forward kinem atics of 6-3 Stewart parallel mechanisms can be expressed asan eight order equation in the end.Finally a specific examp lewas introduced to verify themethod offered herein.
Stewart p latform;parallelmechanism;forward kinematics analysis;orthogonal comp lementmethod;analyticalmethod
TH 112;TP242
1004—132X(2011)05—0505—05
2010—05—13
国防科工委“十一五”预研基金资助项目(C 4220062501);国家自然科学基金资助项目(50375071);航空科学基金资助项目(H 0608-012);江苏省普通高校研究生科研创新计划资助项目(CX 07B-068z)
(编辑 袁兴玲)
程世利,男,1981年生。南京航空航天大学机电学院博士研究生。主要研究方向为并联机构及机械多体系统动力学。吴洪涛(通讯作者),男,1962年生。南京航空航天大学机电学院教授、博士研究生导师。王超群,女,1974年生。南京航空航天大学机电学院博士研究生,南京农业大学工学院讲师。姚 裕,男,1971年生。南京航空航天大学航空宇航学院副研究员、博士。朱剑英,男,1937年生。南京航空航天大学机电学院教授、博士研究生导师。

