POS数据的上下视差误差源检测及误差补偿回归模型
张永军,熊金鑫,熊小东,邓继伟
1.武汉大学遥感信息工程学院,湖北武汉430079;2.铁道第三勘察设计院集团有限公司,天津300251
1 引 言
快速而且正确地恢复摄影时刻像片的空间方位是航空摄影测量的关键技术之一。长期以来,这一目标是通过空中三角测量方法借助大量的地面控制点间接实现。随着传感器技术、空间定位技术和计算机技术的发展,航空摄影测量理论越来越严密、方法越来越先进[1]、所需地面控制点越来越少,正朝着无地面控制的方向发展[2]。
20世纪70年代以后,美国研制成功了新一代卫星无线电导航系统——全球定位系统(GPS),由于它能进行高动态精密三维定位,并可用于在航空摄影的同时确定像片的外方位元素,从而引起了摄影测量界的极大兴趣和普遍关注[3]。在20世纪末出现的定位定向系统(position and orientation system,POS)集差分GPS技术和惯性导航(INS)技术于一体,可在航空摄影时获取航摄像片的6个外方位元素[4],直接用于航空摄影测量影像的定向[5]。已有试验表明,利用POS系统获取的像片外方位元素可以直接制作数字正射影像图[6],而对地形测图而言由于POS系统误差尤其是视准轴误差的存在[7],直接将POS提供的像片外方位元素用于安置元素测图[8]会产生作业员无法忍受的模型上下视差。
本文根据基于POS的相对定向原理,利用实际影像检测POS数据中造成模型上下视差的主要误差源。通过对试验结果进行统计分析,建立系统误差回归补偿模型,在无需区域网平差的情况下,直接通过相对定向消除POS系统误差,使得模型上下视差明显减小,定位精度有较大提高。
2 POS系统误差存在的原因及其分析
根据POS的机理及特点,其系统误差主要由以下几个原因造成:
(1)视准轴误差[9]:POS与航摄仪连接时,需要将IMU固联在航摄仪上,由于安装工艺上的原因,IMU与航摄仪的轴系不可能完全平行,一般来说,两坐标轴系之间总存在着一个小的角度偏差(小于3°);
(2)累积漂移误差[9]:在飞行过程中,由于运动加速度的存在,会形成作用在POS上的惯性干扰力矩,使POS获取数据时产生进动(即漂移),从而引起测量误差,即漂移误差,通常IMU漂移误差对目标定位精度的影响比 GPS漂移误差更大;
(3)GPS失锁和周跳:高精度 GPS卫星导航定位一般是用载波相位测量实现的。而载波相位测量只能测量相位中不足一整周的小数部分,整周部分的连续变化值由多普勒计数得到,飞机侧倾转弯、信号遮挡、信噪比低以及接收机故障等都会引起整周计数突变,称为失周或失锁,也称为周跳。
(4)由像片畸变、地球曲率、大气折光差等引起的误差。
3 基于POS的立体像对相对定向
基于POS的立体像对相对定向以经典摄影测量理论为基础[10],将传统连续像对相对定向与单独像对相对定向相结合,以POS提供的外方位元素作为初值,以左影像的角运动、右影像的直线运动和角运动实现相对定向,其通用误差方程如式(1)所示。由于每个立体像对最多具有5个独立的相对定向元素,因此一般在(φ1,κ1,BY,BZ, φ2,ω2,κ2)中选择5个元素作为定向元素。本文为检测POS数据中造成模型上下视差的主要误差源,采用固定元素法,即在基于POS的立体像对相对定向的通用模型中固定某些相对定向元素,使其不参与平差迭代,只对其他定向元素进行迭代改正。因此固定φ1、κ1,对 BY、BZ、φ2、ω2、κ2进行迭代求解即为基于POS的连续法相对定向;固定BY、BZ,对φ1、κ1、φ2、ω2、κ2进行迭代求解即为基于POS的单独像对相对定向。根据式(1)对相对定向元素进行迭代求解,当改正数小于给定限值时结束迭代。


4 POS系统误差模型的建立及回归分析
文献[11]的研究表明,POS在定位测姿时会产生随航摄飞行时间t呈线性关系的系统误差。在建立误差补偿模型时,假设POS系统误差y与飞行时间t之间的关系为线性关系,即

式(2)代表 y与t的线性回归模型,a0、a1为未知的回归参数;ε为随机误差项。假定t是一个非随机变量,且没有测量误差,通过最小二乘法寻找最优估计量,使得随机误差项ε的平方和达到最小,从而获得回归参数a0、a1。
为检验以上线性回归模型是否真实,应从两个方面进行检验:①线性关系检验,即检验自变量和因变量之间的关系能否用一个线性模型表示;②回归参数检验,即当线性关系检验通过以后,进一步检验每一个自变量对因变量的影响程度是否显著。
相关系数 R2、检验统计量 F0、F0对应的概率P分别是用于检验回归模型正确性的指标和检验参数,其中相关系数R2按下式得到
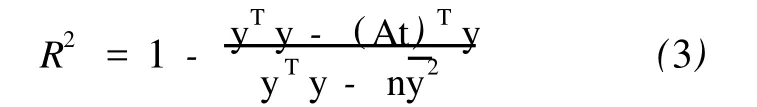

k为未知数个数;F0是服从 F(1,n-m-1)统计检验量,用于检验得到回归变量t对y的影响是否显著。通常 F0越大,变量 t越显著,回归模型的正确性越高。
5 试验结果与分析
5.1 试验影像概述
为了验证本文所述算法的可行性,利用三组实际航空摄影影像数据进行试验,试验影像的资料参数如表1所示。三组试验数据都利用数字摄影测量处理平台DPGrid进行了自动转点与量测,并人工立体量测了全部地面控制点的像平面坐标。

表1 三个试验区航空摄影数据参数描述Tab.1 Image data description of three test areas
5.2 POS数据引起立体模型上下视差的主要误差源检测
在检测POS数据恢复立体模型存在上下视差的主要误差源时,首先需要确定主要误差来源于线元素还是角元素。利用POS提供的外方位元素计算立体模型的上下视差;并根据基于POS的单独像对相对定向,改正φ1、κ1、φ2、ω2、κ2五个角元素,计算相对定向后模型的上下视差;之后采用基于POS的连续法相对定向,左片外方位元素初值采用单独像对相对定向改正后的值,右片仍以POS作为初值,以保证在计算模型上下视差时具有可比性。三种方法恢复立体模型后,统计三组试验数据中每个模型的上下视差中误差,并按航带统计上下视差中误差的最大值、最小值及平均值,统计结果如表2所示。

表2 三种不同方法计算立体模型的上下视差结果对比Tab.2 Comparison among vertical parallaxes of stereo models reconstructed with different methods
从表2的数据可以看出,利用POS提供的外方位元素计算立体模型的上下视差时,试验1中5条航带的上下视差中误差平均值约为22个像素;试验2中9条航带的上下视差中误差平均值约1个像素;试验3中4条航带的上下视差中误差平均值在2个像素以内。经过单独像对相对定向后,试验1中5条航带的上下视差中误差平均值约为0.3个像素;试验2中9条航带的上下视差中误差平均值也为0.3个像素左右;试验3中4条航带的上下视差在0.2个像素以内。而经过连续法相对定向后,模型上下视差与单独像对相对定向试验基本一致。由于两种相对定向方法左片外方位元素一致,单独像对相定向对右片的线元素与角元素均进行改正,而连续法相对定向只对右片角元素进行改正。该试验结果说明POS数据中线元素对模型的上下视差影响很小,其主要误差源在角元素中。
上述试验已经确定POS中造成模型上下视差的主要误差源来自角元素,根据基于POS的连续法相对定向原理,在固定左片方位元素的基础上,分别固定右片的三个角元素、固定φ、固定ω、固定κ,求解其余相对定向元素,计算对应的模型上下视差并与基于POS连续法相对定向结果计算的模型上下视差进行比较,统计结果如图1所示。
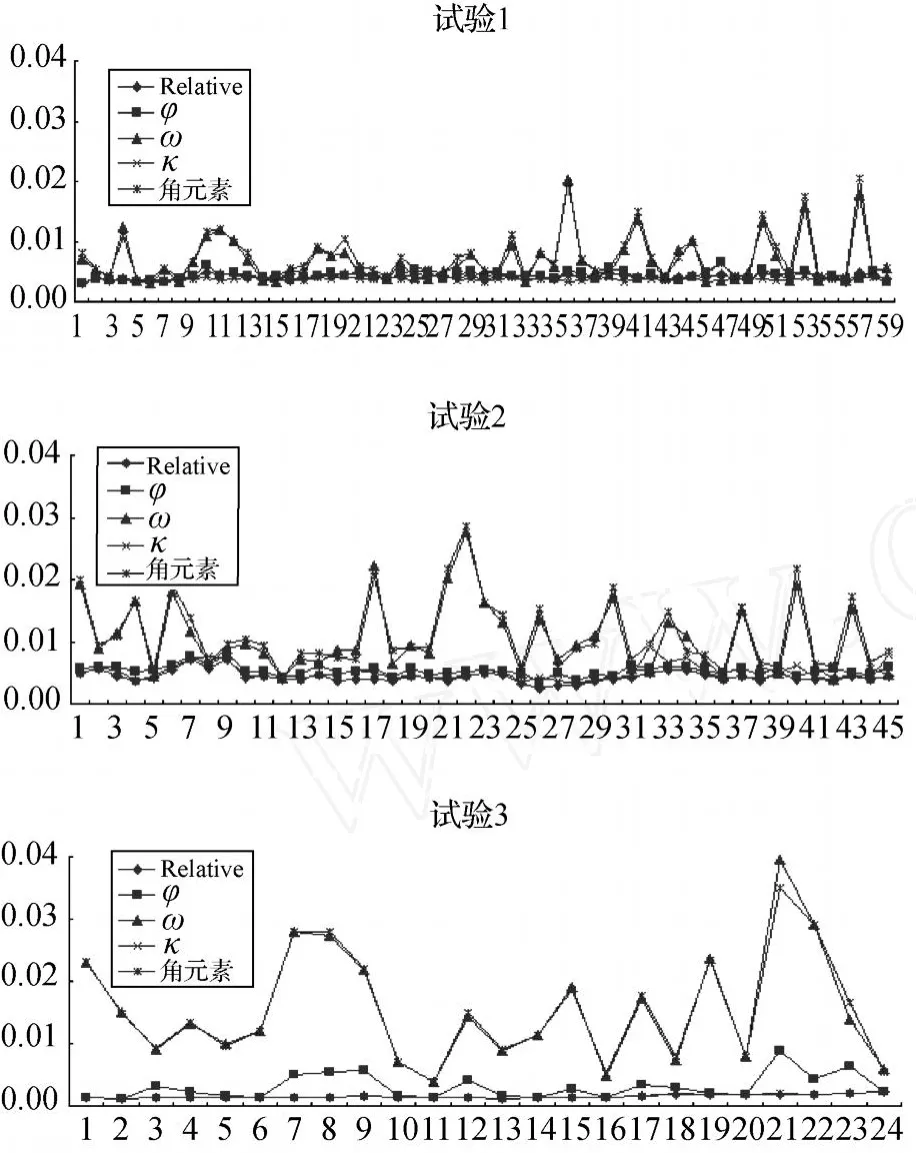
图1 三组试验数据上下视差统计结果对比Fig.1 Comparison among vertical parallaxes of three data sets
图1的三组试验数据当固定模型右片三个角元素时,在迭代过程中只是对线元素进行改正,而角元素的误差不改正;在固定ω时,在迭代过程中对线元素及φ及κ角进行改正,ω角的误差不改正。但从上图可以看出,这两种方式下计算出的模型上下视差非常接近。而固定φ与κ,其结果与步骤一中连续像对相对定向的上下视差非常接近。从而说明在POS数据中,角元素中包含的误差主要集中于ω角,也就是说ω角是造成模型上下视差的主要误差源。
5.3 POS数据系统误差补偿模型
将三组试验测区相对定向后的POS数据与原始POS数据进行对比,计算出POS观测值的三个外方位角元素(φ、ω、κ)的误差。对三组试验的POS观测值中三个外方位角元素误差与时间t进行线性回归分析,得到如图2的统计结果。可以看出φ和κ角的系统误差未呈现出线性关系,而ω的系统误差线性关系比较明显。

图2 POS角元素观测值误差对时间t的回归分析Fig.2 Regression analysis between observation errorofangelelementof POS data and flying time
通过POS观测值中φ、ω、κ误差回归分析结果对整个测区建立误差补偿模型,如表3所示。按照表3中回归模型分别对三个角元素进行改正,用改正后的POS数据计算模型上下视差,将所得对应结果分别与相对定向后、原始POS数据求得的上下视差结果进行比较,如图3所示。

表3 POS观测值中φ、ω、κ误差回归分析结果表Tab.3 Regression analysis of observation error ofφ,ω andκ
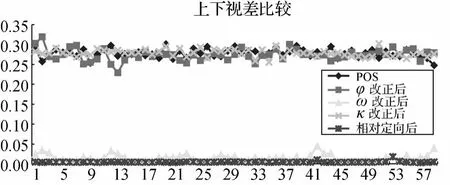
图3 各角元素补偿改正后求得的模型上下视差比较图Fig.3 Comparison among vertical parallaxes of POS data corrected by angle regression model
从上述图表结果可以看出,φ和κ角与时间t无明显回归关系,各时间t的误差点离散地分布在回归直线附近,且利用相应回归模型改正后,模型上下视差无明显减小。而ω角误差与时间t成明显线性回归关系,其相关系数 R2非常接近于1,检验统计量 F0也很大,利用该回归模型改正后,模型上下视差明显减小。
将三组试验区的控制点作为检查点,分别利用原始 POS数据、ω角误差补偿模型改正后的POS数据进行前方交会,表4列出了所有控制点在消除平移误差后前方交会结果与外业测量坐标的较差。可以看出,改正后的POS数据前方交会获得的检查点平面精度和高程精度分别提高了0.5~1.0倍和1.0~2.0倍,完全满足1∶10 000比例尺正射影像制作的要求。

表4 原始POS数据和改正后的POS数据前方交会结果Tab.4 Comparison between results of forw ard intersection with original and rectified POS data m
6 结 论
本文对POS数据引起模型上下视差的主要误差源进行了检测,成功建立了误差补偿模型,并证明了该模型的正确性与可行性。利用1∶78 000、1∶72 000和1∶83 000三种摄影比例尺的航空摄影影像进行试验的结果表明:
(1)POS系统提供的影像外方位元素中,线元素误差对模型的上下视差影响较小,ω角误差是造成模型上下视差的主要误差源。
(2)建立了角元素的误差补偿模型,通过回归分析及控制点前方交会试验证明ω角误差补偿模型可以很好地对ω角进行改正,消除其系统误差。
(3)POS数据ω角系统误差改正后,无需区域网平差即可满足1∶10 000比例尺正射影像制作的精度要求;但由于其他元素的误差没有改正,因此改正结果不能完全满足1∶10 000比例尺立体测图精度的要求。作者进行过试验验证,基于上述三组数据进行POS辅助的无控制点区域网平差后获得的方位元素均可完全满足立体测图精度要求。
正是由于POS系统提供的像片外方位元素在用于实际航测地形测图生产时会产生作业员无法忍受的模型上下视差,因此POS数据只能用于制作数字正射影像图,而无法用于地形测图。本文研究一种行之有效的模型上下视差消除方法,提高了POS数据的定位精度,对于充分发挥POS系统的作用并更好地服务于困难地区的基础地理信息获取有一定意义。
[1] ACKERMANN F.Practical Experience with GPS-supported Aerial Triangulation[J].Photogrammetric Record,1994, 16(84):861-874.
[2] YUAN Xiuxiao.POS-supported Bundle Block Adjustment [J].Acta Geodaetica et Cartographica Sinica,2008 37(3): 342-348.(袁修孝.POS辅助光束法区域网平差[J].测绘学报,2008,37(3):342-348.)
[3] YUAN Xiuxiao,LI Deren.Some Investigation for GPS-supported Aerotriangulation [J]. Acta Geodaetica et Cartographica Sinica,1997,26(1):14-19.(袁修孝,李德仁.GPS辅助空中三角测量的若干探讨[J].测绘学报, 1997,26(1):14-19.)
[4] YUAN Xiuxiao.Analysis of Y-parallax of Stereo Model Reconstructed Using Elements ofExteriorOrientation Determined by Position and Orientation System [J]. Geomatics and Information Science of Wuhan University, 2007,32(10):856-859.(袁修孝.POS数据用于立体模型恢复时的上下视差分析[J].武汉大学学报:信息科学版,2007,32(10):856-859.)
[5] GREENING T,SCHICKLER W,THORPE A.The Proper Use of Directly Observed Orientation Data:Aerial Triangulation is Not Obsolete[C]∥Proceedings of 2000 ASPRS Annual Conference.Washington DC:ASPRS,2000.
[6] GRUEN A,BAER S.Aerial Mobile Mapping—Georeferencing without GPS/INS[C]∥Proceedings of the 3rd International Symposium on Mobile Mapping Technology. Cairo:[s.n.],2001.
[7] JACOBSEN K,WEGMANN H.Dependencies and Problems of Direct Sensor Orientation[C]∥Proceedings of the OEEPE Workshop on Integrated SensorOrientation. Hannover:[s.n.],2001.
[8] CRAMER M,STALLMAN D.System Calibration for Direct Georeferencing[J].International Archives of Photogrammetry and Remote Sensing,2002,34:79-84.
[9] HONKAVAARA E.Calibration Field Structures for GPS/ IMU/Camera-system Calibration[J].The Photogrammetric Journal of Finland,2003,18(2):3-15.
[10] WAN G Zhizhuo.Principles of Photogrammetry[M]. Beijing:Surveying and Mapping Press,1990.(王之卓.摄影测量原理[M].北京:测绘出版社,1990.)
[11] ACKERMANN F.GPS for Photogrammetry[C]∥Proceedings of Tutorial on Mathematical Aspects of Data Analysis.[S.l.]:ISPRS.1991:17-70.

