三峡库区对局地暴雨和江面大风影响的理论模型
卢晨晨,陆维松,陶丽,邵海燕,陈少平
(1.南京信息工程大学大气科学学院,江苏南京210044;2.解放军理工大学气象学院,江苏南京211101;3.湖北省气象局,湖北武汉430074)
0 引言
三峡水利枢纽位于长江西陵峡中段,工程完工后将形成一个坝高185 m,水面面积为1 150 km2,蓄水量达393亿m3的巨大水库。正常运行期水库水位将达到175 m,库区水位的大幅度上升和水库水面的形成,将大大改变该区域的原有下垫面,而下垫面的改变将对局地天气造成影响,特别是对暴雨和江面大风形成和发展影响很大,而暴雨和江面大风是三峡库区的重大自然灾害之一。因此三峡库区对暴雨和江面大风影响的研究具有重要意义。
对于由水陆下垫面热力不均匀所引起的局地环流,人们最早将注意力集中在海陆风的研究上。到了20世纪50年代后期,相继出现对海陆风的数值模拟研究。Pearce(1955)首次用非线性方程模式计算了海风环流的变化。Estoque(1961,1962)以数值方法求解非线性方程,得到了垂直海岸线的海陆风环流随时空变化的风场和温度场,并讨论了盛行风对海陆风的影响及离岸风加强海陆风的现象等结果。McPherson(1970)首次建立了三维海陆风预报模式。Pielke(1974)建立了较完整的海风模式。Morez(1967)将Estoque(1961)建立的海陆风数值模式应用到Michigan湖的湖陆风研究上。Patrinos(1977)、Estoque(1981)、Maddukuri(1982)均采用静力平衡数值模式分别对安大略湖、密执安湖等大型湖泊的局地环流进行了数值模拟。
黄荣辉和严邦良(1989)采用Ogura and Phillips(1962)所提出的非弹性运动方程系建立了一个河陆风变化的数值模式,并利用此模式计算了长江三峡某地段河陆风的日变化,其计算结果符合实际情况。王浩(1993)通过建立大气—水体—土壤模式来研究水体深度的变化对水体的气候效应的影响。张洪涛等(2004)对长江三峡水库气候效应进行了模拟研究,他们建立了一个三维静力平衡的大气—土壤耦合模式,模式详细考虑了复杂地形、植被和水面的热力、动力过程,特别是还详细地考虑了坡度、坡向的影响,但在研究中忽略了水温的日变化。
综合国内外以往关于陆地水体的局地环流研究可知,研究者对于大湖泊等大面积水域的研究较多,而对于小湖泊、河流等小尺度的水体的研究较少,且主要应用数值试验和诊断分析方法,而鲜有利用解析方法从理论上对水体状态对局地环流影响的研究。
Defant(1950)用线性模式,在给定的下边界热力强迫条件下研究了海陆风理论。Martin and Pielke(1983)进一步研究了Defant方程组的解,并得到新的结果。本文在Defant(1950)的海陆风模式中,引入水汽凝结潜热项,并提出新的适用于陆地水体的解,来分析三峡库区水体对局地环流的影响,进而讨论对局地暴雨的影响。
1 基本方程组和其解析解
如图1所示,取x-z平面沿长江流向的法线方向,设中尺度扰动在y方向均匀,不考虑天气尺度背景场的平流作用,则采用与Defant(1950)类似的两维非静力平衡方程组:

式中变量符号均为气象常用符号。λ为1和0时分别对应非静力平衡和静力平衡。上标()'量表示中尺度扰动量;()0表示天气尺度变量。方程组中动量和热量的湍流输送项都已作了简化,σH、σv和K均为常数。为简化,略去天气尺度背景场的水平梯度,并使用不可压缩条件。
为考虑水汽凝结潜热作用,在方程(5)中引入凝结潜热项kw'(Shirer and Dutton,1979;Cho et al.,1993),

其中:

式中:sgnw'为符号函数;T0为温度的典型值;γd和γm分别为干、湿绝热递减率。
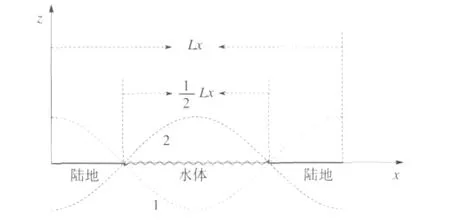
图1 模式示意图Fig.1 Schematic diagram of the mode
w'>0时,k=(θ0/T0)(γd-γm),因总有γd>γm,所以当有上升气流时,即w'>0,kw'>0,使得>0,即参数化考虑上升运动产生的水汽凝结潜热使得大气温度增加;反之,当下沉气流时,即w'<0,k=0,无水汽凝结潜热作用。
方程(5)化为:
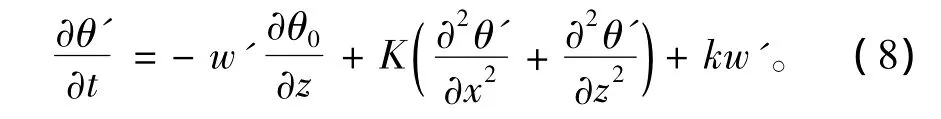
方程(1)—(4)和(8)式的解可取为
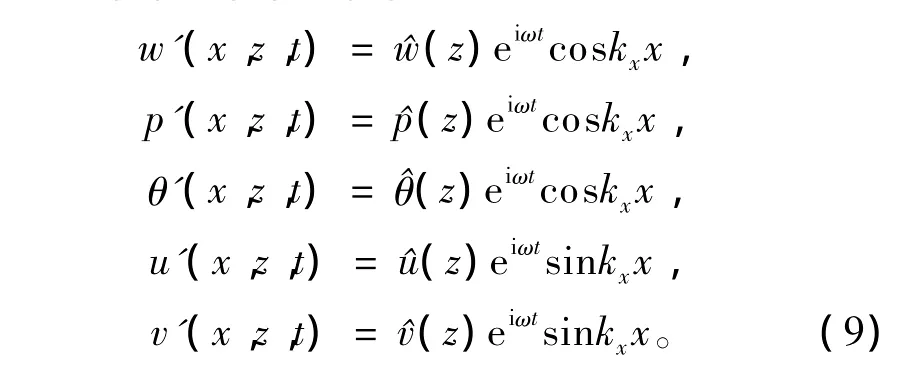
边界条件为:
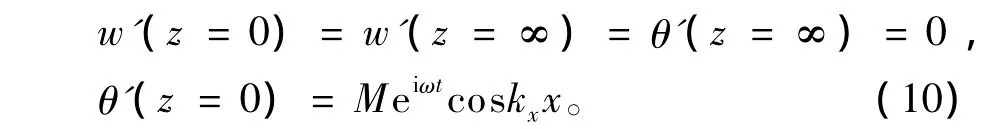
其中:M为中尺度地面位温扰动的振幅。已设各变量在x方向是周期的,x方向波数kx=2π/Lx,Lx为x方向波长。0.25Lx对应水面一侧的陆面的宽度,如图1所见,此陆面上最大加热位于离水面的0.25Lx处,即陆面远离水面的一侧,而0.5Lx对应水面的宽度,水面上最大加热位于离陆面的0.25Lx处。
频率ω表示温度场的周期变化的频率,对应模拟河陆风日变化的频率。即t=0~6,18~24对应白天;而t=6~18对应夜晚;t=0对应日出后6 h,为白天因接受太阳辐射加热陆面温度最高的时刻;而t=12对应日落后6 h,为江面最暖的时刻。
由方程组(1)—(4)、(8)和边界条件(10)可看出,u'、v'和w'、p'、θ'位相相差90°,因为前两个变量是由后3个变量的导数来表示的。
将(9)式代入方程(1)—(4)和(8)中,得到一组线性常微分方程:

(11)式中5个方程可合并为^θ的一元四阶
方程

式中:
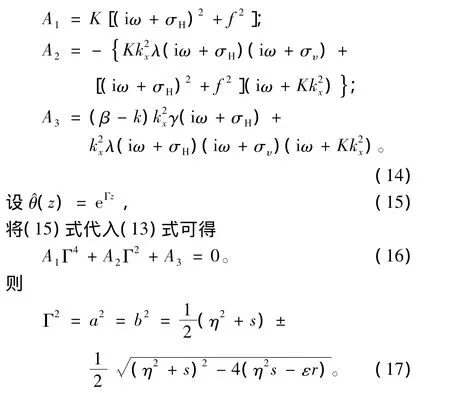
式中:

取
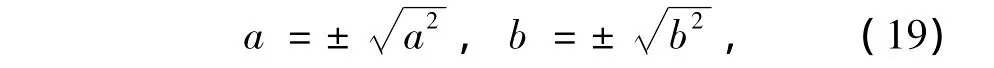
设
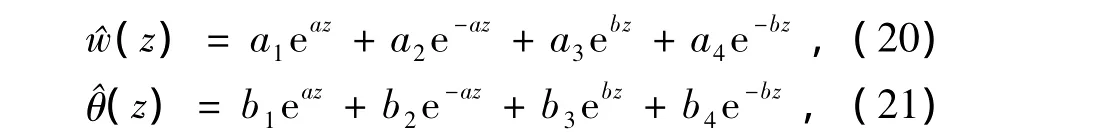
取
小学生所获得的认知经验基本上都是通过学校教育与生活实践得到的,而小学数学教师优化课堂提问的基本手段便是从小学生的现实生活入手。提出生活化的数学问题,让小学生借助自己的生活经验分析问题,确定数学问题的解题模型,然后再通过一系列数学探究与知识阐述提炼出生活中的数学规律,保证小学生的思维状态一直都是积极的、主动的、发散的。
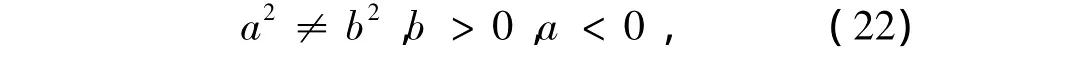
利用z=∞时边界条件(10)式,则(20)和(21)式中为保持w'、θ'的有界性,有

将(23)式代入(20)和(21)式后,并利用z=0时边界条件(10)式,可得
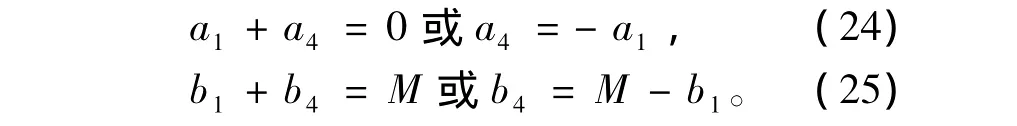
将(23)、(24)和(25)式代入(20)和(21)式,可得

将(26)、(27)式代入(11)式中第5式,得

式中:
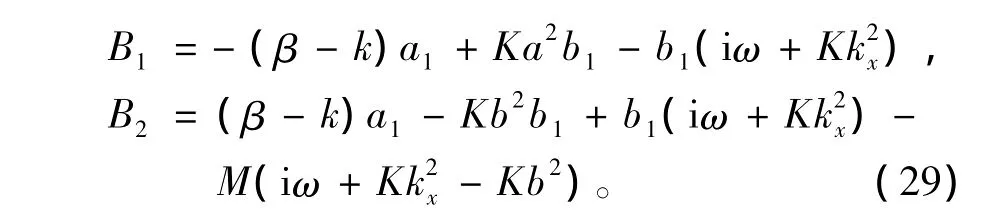
因为a≠-b,若使(28)式对任意z成立,则必须同时成立,即得

(30)式中两式相加,可得

将(31)式代入(30)第1式,可得
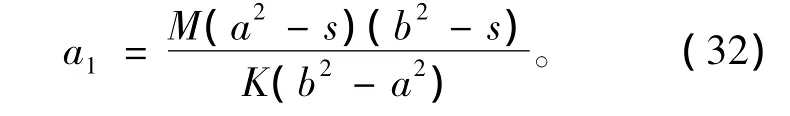
利用(17)式,(32)式可化为

将(31)和(33)式代入(26)和(27)式中,得
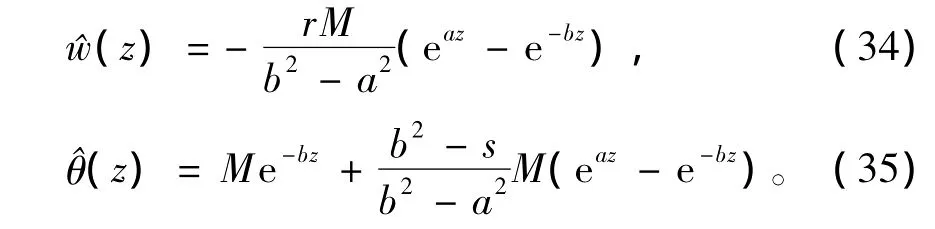
利用(34)和(35)式,由(11)式的第4、2、1式可得:
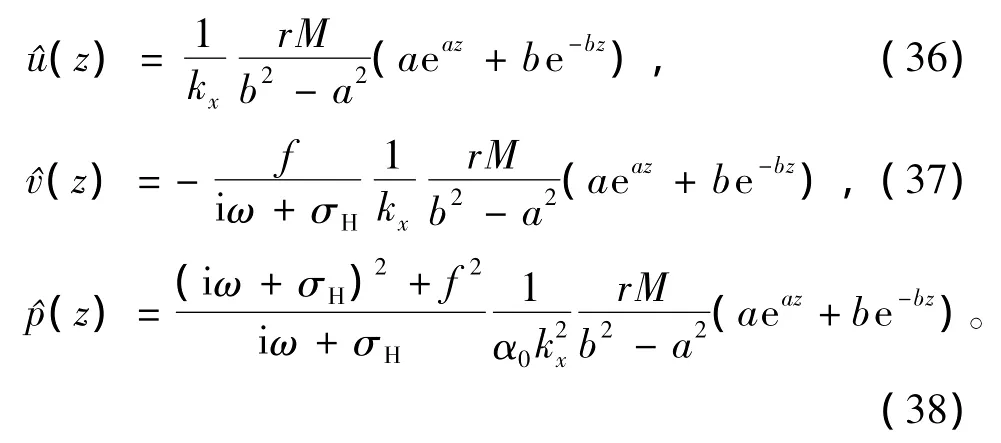
将(34)—(38)式代入(9)式,即考虑水汽凝结潜热加热时二维非静力平衡方程组(1)—(4)和(8)式的解析解。取变量w'、p',θ'、u'、v'的实部作为其实际的解析解,此解析解是x、z、t的函数,解的值需利用各参数和变量η2、r、s、ε、a、b和k的值计算(9)、(35)—(39)、(18)—(20)式的实部才能得到。为了图示说明方程组的解析解(35)—(39)式,取模式参数数值如下:

2 计算结果与分析
由(12)式可得
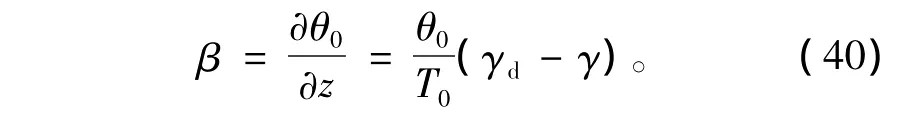
当w'>0时,利用式(6)和(7),得

其中:k为凝结潜热系数;γd、γm、γ分别为干绝热减温率、湿绝热减温率、大气垂直减温率。
由(40)式和(41)式,可得
1)当γd>γ>γm时,有k>β>0,对应大气层结条件不稳定;
2)当γ<γm时,有k<β,对应大气层结绝对稳定;
3)当γ>γd时,因总有γd>γm,则有k>0,β<0,即k>β,对应大气层结绝对不稳定。
在此模式中,对k分别取11个不同的值进行计算:0,0.1,0.3,0.5,0.7,0.9,1.0,1.2,1.5,1.8,2.0℃·km-1。
在图2—6中,横坐标代表垂直于江岸的水平距离(0~30 km),0~7.5 km为陆地,7.5~22.5 km为水体,22.5~30 km为陆地;纵坐标代表铅直距离(0~2 000 m)。
2.1 无水汽凝结潜热的情况
图2分别给出k=0,即不考虑水汽凝结潜热时的u'、w'和u'-w'场。
计算结果表明:1)u'场。在00—06时和18—24时(06—18时),在0~320 m的低层,出现江风或向岸风(陆风或离岸风),而在320~1 670 m的中层,出现了向江中心辐合的离岸风(向两岸辐散的向岸风)。如图2a所示,在t=0时,低层和中层u'分别出现正负极大值,其绝对值为14.3和2.8 m·s-1,t=12时与t=0时情况相同。
2)w'场。在00—06时和18—24时(06—18时),在0~1 350 m的低层,在两岸陆地上方,w'>0,为上升气流(w'<0,为下沉气流);而在水体上方,w'<0,为下沉气流(w'>0,为上升气流)。如图2b所示,在t=0时,低层w'出现正负极大值绝对值为0.38 m·s-1。
3)u'-w'流场。在00—06时和18—24时(06—18时),在垂直方向上,均出现两个环流对。在0~1 350 m的低层,出现两个对偶且环流相反的江风(陆风)环流。在z=300~1 350 m的返回气流随高度逐渐减小,且远小于z=0~300 m的江陆风气流。在1 350~20 000 m的上层,也出现一对环流相反的环流。图2c、d分别为t=0和12 h时的u'-w'流线场。
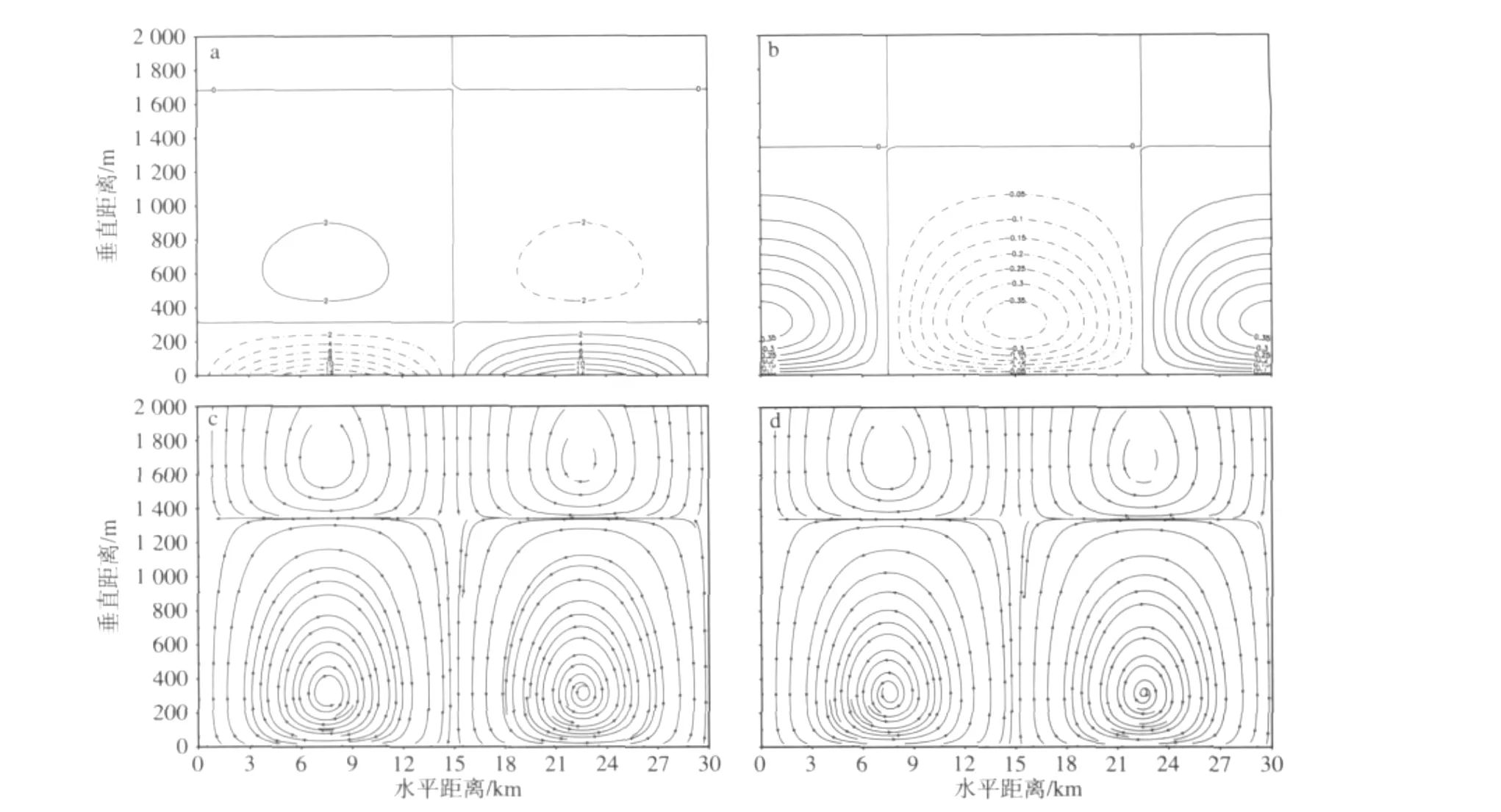
图2 k=0时,t=0时的u'场(a)、w'场(b)和t=0(c)、t=12 h(d)时的u'-w'场(单位:m·s-1)Fig.2 With k=0,the(a)horizontal and(b)vertical velocity fields when t=0;the u'-w'streamline field when(c)t=0 and(d)t=12 h(units:m·s-1)
2.2 有水汽凝结潜热的情况
2.2.1 0<k<1.0℃·km-1时的u'、w'和u'-w'场
k<β=1.0℃·km-1,有γ<γm,对应大气层结绝对稳定。
1)k=0.5℃·km-1
计算结果表明:1)u'场。在00—06时和18—24时(06—18时),在两岸陆面和江面上,分别在z=0~380或320 m的低层,出现江风(分别在z=0~320或380 m的低层出现陆风),而在z=380~1 720 m的中层和z=320~2 000 m的上层,出现的离岸风(在z=320~2 000 m的上层和z=380~1 680 m的中层为向岸风)。如图3a、b所示,在t=0和12时,在低层和中上层u'均出现正负极大值,其绝对值均为14.3和3.1 m·s-1。中层u'和低层u'相比大大减小。可见,两岸陆面上方江风环流中层离岸风高度比江面上方陆风环流对应向岸风高度高。
2)w'场。在00—06时和18—24时(06—18时),在z=0~1 680 m(或1 350 m)的低层,在两岸陆地上方,w'>0,为上升气流(w'<0,为下沉气流);而在水体上方,w'<0,为下沉气流(w'>0,为上升气流)。如图3c、d所示,在t=0和12时,低层w'出现正负极大值为0.51 m·s-1和-0.38 m·s-1。由此可见,江风环流低层上升气流高度比陆风环流对应高度高330 m。
3)u'-w'流场。在00—06时和18—24时(06—18时),在垂直方向上,均出现两个环流对。在z=0~1 680 m(或1 350 m)的低层,出现一对环流相反的江风(陆风)垂直环流。在z=370~1 680 m(z=320~1 350 m)的返回气流仍随高度逐渐减小,且远小于z=0~370 m(或320 m)低层的江陆风气流。在z=1 680(或1 350)~2 000 m的上层,也出现一对环流相反的环流,陆风上层环流明显比江风上层环流强。图3 e、f分别为t=0和12 h时的u'-w'流线场。
由上可见,江风环流对应的低层上升气流的高度和中层离岸风高度均分别比陆风环流这两种高度高,显然,江风环流比陆风环流强。
与k=0时相比,k=0.5℃·km-1时的中上层u'大0.3 m·s-1,增大11%,低层w'正极大值大0.13 m·s-1,增大26%。可见,k=0.5℃·km-1时江陆风环流比k=0时有所增强。
2)k=0.9℃·km-1
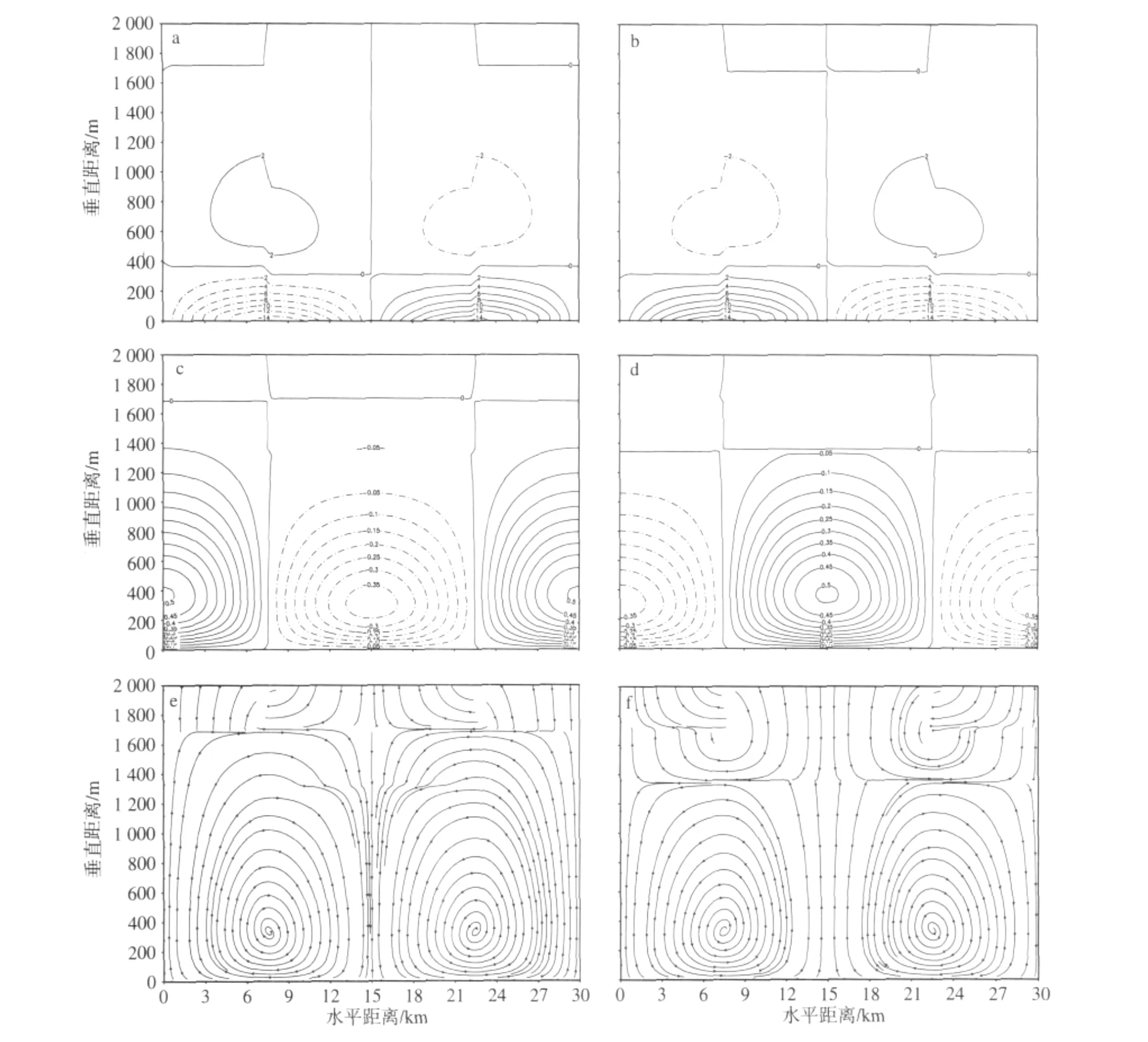
图3 k=0.5℃·km-1时,t=0时的u'(a)、w'(c)和u'-w'(e)场以及t=12 h时的u'(b)、w'(d)和u'-w'(f)场(单位:m·s-1)Fig.3 With k=0.5℃·km-1,the horizontal field when(a)t=0 and(b)t=12 h;the vertical velocity field when(c)t=0 and(d)t=12 h;the u'-w'streamline field when(e)t=0 and(f)t=12 h(units:m·s-1)
计算结果表明:1)u'场。在00—06时和18—24时(06—18时),在两岸陆面和江面上,分别在z=0~500 m或320 m的低层,出现江风(分别在z=0~320 m或500 m低层,出现陆风),而在z=500 m或320~2 000 m的上层,出现的离岸风(在z=320 m或500~1 680 m的中层为向岸风)。如图4a、b所示,在t=0(12)时,低层u'出现正负极大值,其绝对值均为17.8(17.7)m·s-1,而中上层u'均出现两个正负极大值,正负极大值的绝对值均为2.8(2.8)m·s-1。中上层u'比低层u'均大大减小。可见,江风环流上层离岸风高度比陆风环流对应高度高320 m。
2)w'场。在00—06时和18—24时(06—18时),在两岸陆面上方,分别在z=0~2 000 m整层,有w'>0,为上升气流(z=0~1 340 m的低层,有w'<0,为下沉气流),而在水面上方,在z=0~2 000 m整层,有w'<0,为下沉气流(z=0~1 350 m的低层,有w'>0,为上升气流)。
如图4c、d所示,在t=0(12)时,整层出现两正极大值,为0.82 m·s-1(一正极大值,为0.82 m·s-1),两负极大值,为-0.38和-0.42 m·s-1(一负极大值,为-0.38 m·s-1)。可见,在两岸陆面上方,江风环流整层上升气流高度比陆风环流对应高度高660 m,而在江面上方,两者高度接近相等。
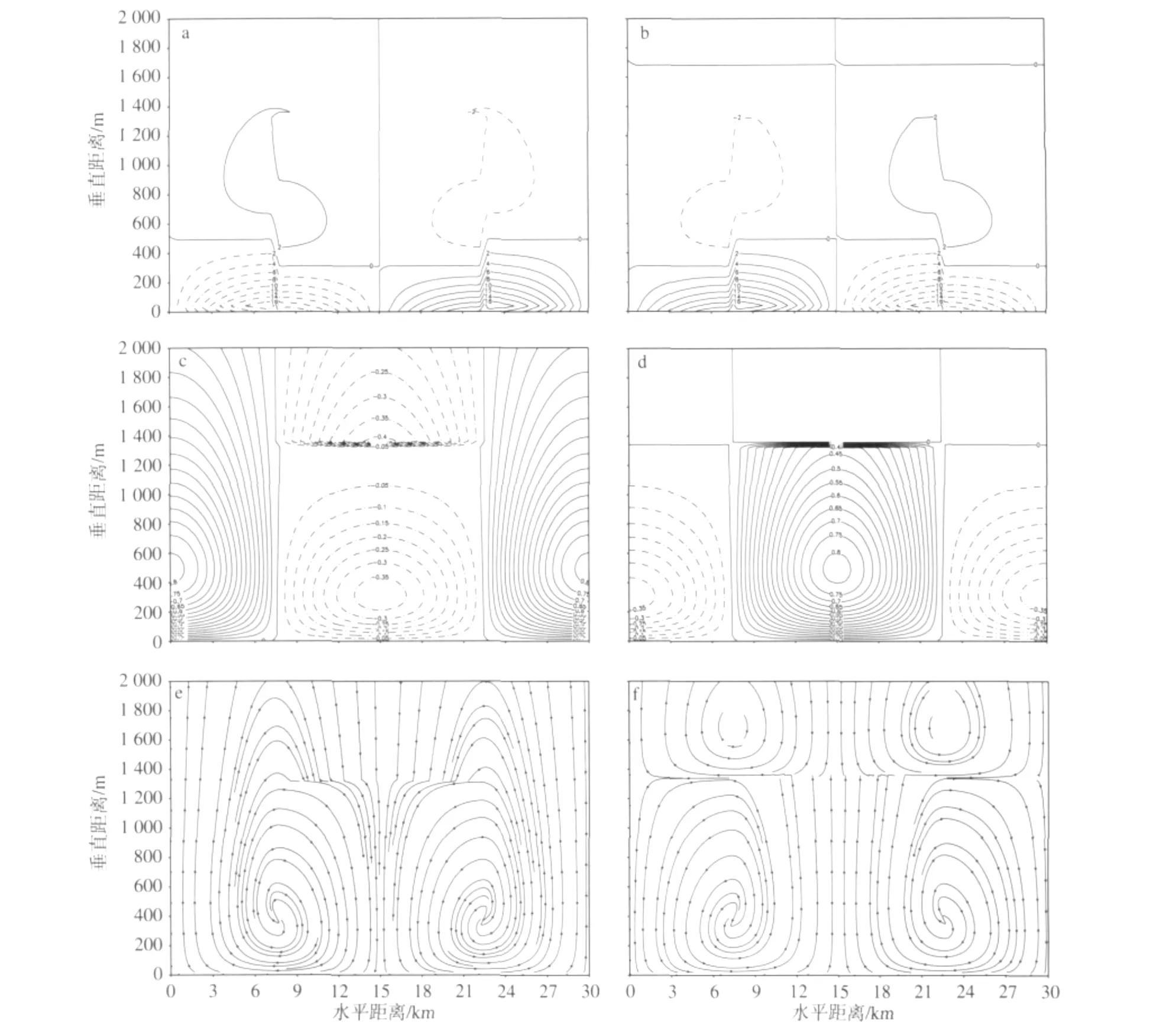
图4 k=0.9℃·km-1时,t=0时的u'(a)、w'(c)和u'-w'(e)场以及t=12 h时的u'(b)、w'(d)和u'-w'(f)场(单位:m·s-1)Fig.4 With k=0.9℃·km-1,the horizontal field when(a)t=0 and(b)t=12 h;the vertical velocity field when(c)t=0 and(d)t=12 h;the u'-w'streamline field when(e)t=0 and(f)t=12 h(units:m·s-1)
3)u'-w'流场。在00—06时和18—24时(06—18时),在垂直方向上,仅陆风环流出现两个环流对。在z=0~2 000 m(或1 350 m),仍出现一对环流相反的江风(陆风)垂直环流。在z=350~2 000 m(或1 350 m)的返回气流随高度逐渐减小,且远小于z=0~350 m(或350 m)低层的江陆风气流。在整层江陆风环流中心附近流线出现了间断,是由于中心两侧垂直上升和下沉气流对应的水汽凝结加热不同所引起的与锋面类似的间断面。在陆风环流z=1 350~2 000 m的上层,也出现一对环流相反的环流。图4e、f分别为t=0和12时的u'-w'流线场。
可见,江风环流的整层上升气流高度和上层离岸风高度均分别比陆风环流这两种高度高得多。显然,仍有江风环流比陆风环流要强得多。
与k=0和0.5℃·km-1时相比,k=0.9℃·km-1时低层u'极大值绝对值均大3.5 m·s-1,增大24%;而k=0.9℃·km-1时,中上层u'极大值绝对值小0~0.3 m·s-1,减小0~10%。k=0.9℃·km-1时的整层、低层w'正极大值增大0.44和0.31 m·s-1,增大116%和61%。
综上所述,与k=0和0.5℃·km-1情况相比,k=0.9℃·km-1的江陆风环流大大增强。
2.2.2 k=1.0℃·km-1时的u'、w'和u'-w'场
k=β=1.0℃·km-1,有γ=γm,对应大气层结中性稳定。
计算结果表明:1)u'场。在00—06时和18—24时(06—18时),在两岸陆面和江面上,分别在z=0~380或320 m的低层,出现江风(分别在z=0~320或380 m的低层,出现陆风),而在z=380~1 680 m和z=320~1 950 m的中层,出现离岸风(在z=320~1 950 m和z=380~1 680 m的中层为向岸风)。如图5a、b所示,在t=0(12)时,低层u'出现正负极大值,其绝对值均约为17.4 m·s-1(17.4 m·s-1),而中层u'出现正负极大值,其绝对值均为4.2 m·s-1(4.2 m·s-1),可见,江风中层u'均比陆风中层u'略强。中层u'与低层u'相比明显减小。
2)w'场。在00—06时和18—24时(06—18时),在两岸陆面上,在z=0~1 280 m的低层,有w'>0,为上升气流(在z=0~1 320 m的低层,有w'<0,为下沉气流),而在江面上方,在z=0~1 280 m的低层,有w'<0,为下沉气流(在z=0~1 320 m的低层,有w'>0,为上升气流)。如图5c、d所示,在t=0(12)时,低层w'出现正极大值,为0.60 m·s-1(0.60 m·s-1),其负极大值为-0.38 m·s-1(-0.38 m·s-1)。可见陆风环流的低层上升气流高度比江风环流对应高度要高40 m。
3)u'-w'流场。在00—06时和18—24时(06—18时),在垂直方向上,均出现两个环流对。在z=0~1 280 m(或1 320 m)的低层,出现一对环流相反的江风(陆风)垂直环流。在z=380~1 320 m(或1 320 m)的返回气流随高度减小,且远小于z=0~380 m(z=0~380或350 m)的低层江陆风环流。在z=1 280~2 000 m(或2 000 m)的上层,也出现一对环流相反的环流。图5e、f分别为t=0和12时的u'-w'流线场。

图5 k=1.0℃·km-1时,t=0时的u'(a)、w'(c)和u'-w'(e)场以及t=12 h时的u'(b)、w'(d)和u'-w'(f)场(单位:m·s-1)Fig.5 With k=1.0℃·km-1,the horizontal field when(a)t=0 and(b)t=12 h;the vertical velocity field when(c)t=0 and(d)t=12 h;the u'-w'streamline field when(e)t=0 and(f)t=12 h(units:m·s-1)
可见,陆风环流的上升气流高度和上层离岸风高度均比江风环流对应的这两种高度高一点。显然,此时陆风环流比江风环流稍强一些。
与k=0、0.5和0.9℃·km-1时相比,k=1.0℃·km-1时,中层u'极大值绝对值增大,低层u'极大值绝对值增大。而四者低层w'负极大值均相同。k=1.0℃·km-1时江风环流w'的低层高度均低得多。k=1.0℃·km-1时陆风环流w'的低层高度均相等。
综上所述,k=1.0℃·km-1时的江陆风垂直环流,比k=0和0.5℃·km-1时强和稍强,而比k=0.9℃·km-1时明显弱得多。
2.2.3 k=1.5℃·km-1时的u'、w'和u'-w'场
k>β=1.0℃·km-1,有γd>γ>γm,对应大气层结条件不稳定。
计算结果表明:1)u'场。在00—06时和18—24时(06—18时),在两岸陆面和江面上,分别在z=0~170或320 m的低层,出现江风(在z=0~320或170 m的低层,出现陆风)。而在z=170~950或950 m的中层,出现离岸风(在z=320~1 320 m和z=170~1 690 m的中层为向岸风)。如图6a、b所示,在t=0(12)时,在低层,u'出现正负极大值,其绝对值均约为14.3 m·s-1(14.3 m·s-1),而在中层,u'出现正负极大值,其绝对值均约为6.5 m·s-1(两对正负极大值绝对值分别为5.9和2.8 m·s-1)。可见,江风环流上层离岸风高度比陆风环流对应高度要低370和740 m,高度降低约39%和78%。

图6 k=1.5℃·km-1时,t=0时的u'(a)、w'(c)和u'-w'(e)场以及t=12 h时的u'(b)、w'(d)和u'-w'(f)场(单位:m·s-1)Fig.6 With k=1.5℃·km-1,the horizontal field when(a)t=0 and(b)t=12 h;the vertical velocity field when(c)t=0 and(d)t=12 h;the u'-w'streamline field when(e)t=0 and(f)t=12 h(units:m·s-1)
2)w'场。在00—06时和18—24时(06—18时),在两岸陆面上,在z=0~380 m低层,有w'>0,为上升气流(在z=0~1 320 m低层,有w'<0,为下沉气流),而在江面上方,在z=0~380 m低层,有w'<0,为下沉气流(在z=0~1 320 m低层,有w'>0,为上升气流)。如图6c、d所示,在t=0(12)时,低层出现正负极大值,为0.16和-0.38 m·s-1(两个正极大值,为0.37、0.16 m·s-1,和一负极大值,为-0.38 m·s-1)。可见陆风环流的低层上升气流高度比江风环流对应高度约高940 m,增大2.5倍。
3)u'-w'流场。在00—06时和18—24时(06—18时),在垂直方向上,出现3个(2个)环流对。在z=0~380 m(或1 320 m)的低层,出现一对环流相反的江风(陆风)垂直环流,在z=200~380 m(或1 320 m)的返回气流随高度减小,且小于z=0~200 m(或200 m)的低层江陆风环流。在低层江陆风环流中心附近流线出现了由于水汽凝结加热不同所引起的与锋面类似的间断面。在z=380~1 620 m和z=1 620~2 000 m(z=1 320~2 000 m)的中上层,也出现两个(一个)环流相反的环流对。图6e、f分别为t=0和12时的u'-w'流线场。
可见,陆风环流所对应的上升气流的高度和上层离岸风高度均比江风环流对应的这两种高度高得多。显然,陆风环流比江风环流要强得多。
与k=0、0.5、0.9和1.0℃·km-1时相比,k=1.5℃·km-1时,中层u'极大值绝对值增大,而低层u'极大值绝对值减小。k=1.5℃·km-1时低层w'正极大值,在t=0时分别减小约0.22~0.66 m·s-1;在t=12时,分别减小约0.01~0.45 m·s-1。4种k值低层w'负极大值均相同。k=1.5℃·km-1时江风环流低层高度均低得多。而这4种k值的陆风环流低层高度基本相同。
综上所述,k=1.5℃·km-1时江陆风垂直环流均比k=0、0.5、0.9和1.0℃·km-1时大大减弱。
2.2.4 β=0~2.0℃·km-1时的u'、w'和u'-w'场
低层江风u'正负极大值的绝对值如表1所示。当0≤k≤0.5℃·km-1时,u'均为14.3 m·s-1;当k由0.5℃·km-1增大到0.9℃·km-1时,u'由14.3 m·s-1逐渐增大到17.8 m·s-1;当k由0.9℃·km-1增大到1.1℃·km-1时,u'由17.8 m·s-1逐渐减小为14.3 m·s-1;当1.1℃·km-1≤k≤2.0℃·km-1时,u'仍均为14.3 m·s-1。低层陆风正负极大值的绝对值随k的变化与江风相同。

表1 k=0~2.0℃·km-1时,u'场的特征参数Table 1The characteristic parameters of the horizontal velocity field when k=0—2.0℃·km-1
当k由0增大到0.9℃·km-1时,低层陆面上方江风u'场高度由320 m逐渐增大到500 m;当k由0.9℃·km-1增大到2.0℃·km-1时,低层陆面上方江风u'场高度由500 m逐渐减小到140 m。当0≤k≤2.0℃·km-1时,低层江面上方陆风u'场高度变化与低层陆面上方江风相似。低层陆面上方江风u'场高度,在0≤k≤2.0℃·km-1时,均为320 m。
当0≤k≤0.4℃·km-1时,中上层陆面上方江风u'场回流高度均为1 680 m;当k由0.4增大到0.7℃·km-1时,中上层陆面上方江风u'场回流高度由1 680 m逐渐增大到约2 000 m;当0.7℃·km-1≤k≤0.9℃·km-1时,中上层陆面上方江风u'场回流高度均为约2 000 m;而当k从0.9增大到2.0℃·km-1时,中上层陆面上方江风u'场回流高度由2 000 m逐渐减小到820 m。当0≤k≤2.0℃·km-1时,中上层江面上方江风和陆面上方陆风两者回流高度变化均与陆面上方江风情况相似,而中上层江面上方陆风回流高度均为1 680 m。
低层江风w'正极大值如表2所示。当k由0增大到0.9℃·km-1时,w'由0.38逐渐增大到0.82 m·s-1;k由0.9增大到2.0℃·km-1时,w'由0.82逐渐减小到0.12 m·s-1。0≤k≤1.1℃·km-1时,低层陆风w'正极大值的变化与低层江风相似;而当k由1.1增大到2.0℃·km-1时,w'由0.29逐渐增大到0.38 m·s-1。而低层江陆风w'负极大值的绝对值,在0≤k≤2.0℃·km-1时,均为0.38 m·s-1。
当k由0增大到0.9℃·km-1时,低层江风w'场高度由1 350 m逐渐增大到约2 000 m;当k由0.9增大到2.0℃·km-1时,低层江风w'场高度由2 000 m逐渐减小到330 m。而低层陆风w'场高度,在0≤k≤2.0℃·km-1时,均为1 350 m。
3 结语
从考虑水汽凝结潜热作用的两维非静力平衡方程组出发,利用江河陆地的下边界条件,从理论上,求得适用于陆地水体的解析解,以此来分析三峡库区水体的改变对局地环流的影响,得到如下结论。
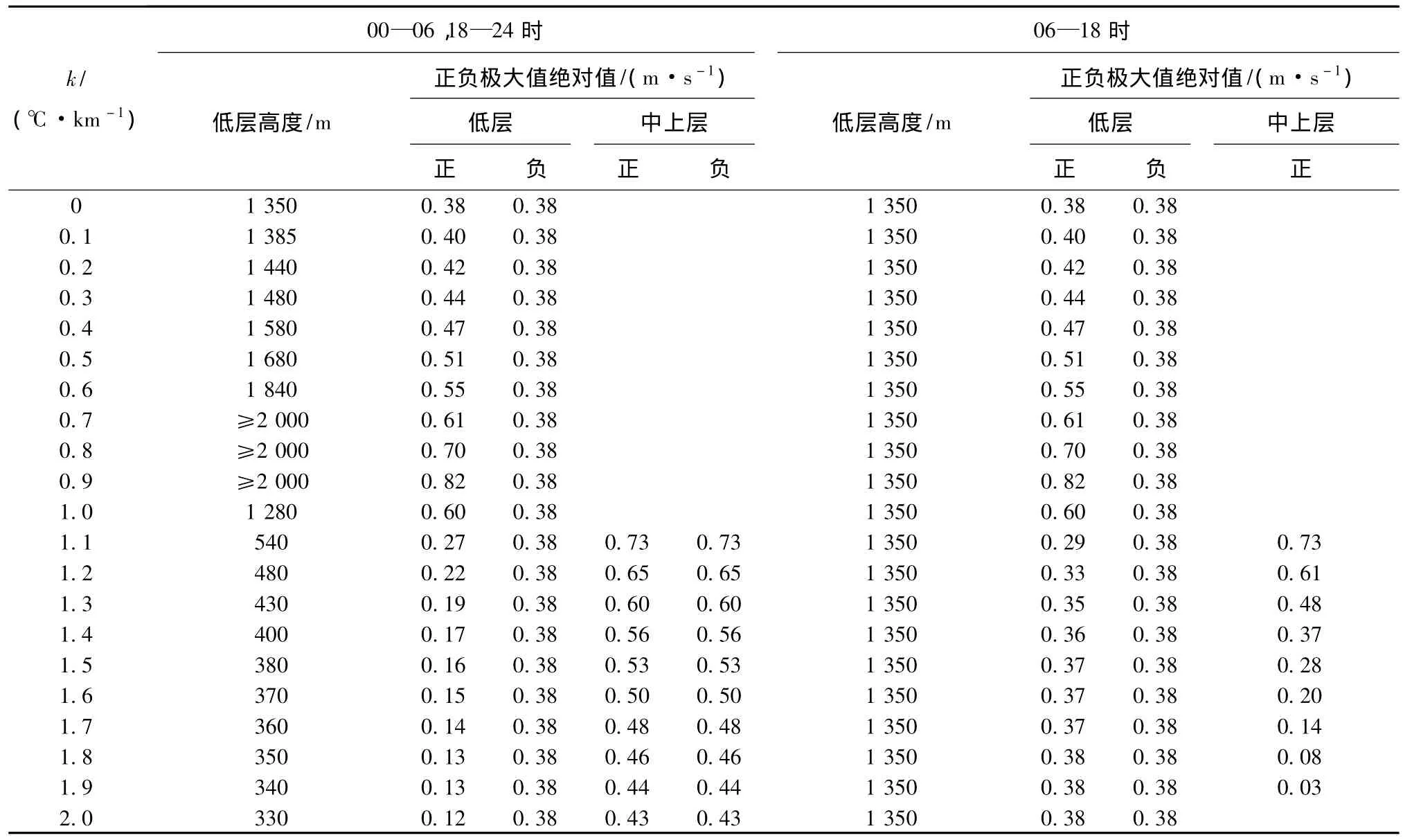
表2 k=0~2.0℃·km-1时,w'场的特征参数Table 2The characteristic parameters of the vertical velocity field when k=0—2.0℃·km-1
1)与不考虑水汽凝结潜热k=0时江风和陆风垂直环流两者具有对称性不同,考虑水汽凝结潜热k≥0时江风和陆风垂直环流两者具有不对称性。
当0<k<β=1℃·km-1,有γ<γm,对应大气层结绝对稳定时,江风垂直环流比陆风垂直环流强,且随着k由0增大到1℃·km-1,江风环流比陆风环流强。
当k>β=1℃·km-1,有γd>γ>γm,对应大气层结条件不稳定时,江风垂直环流比陆风垂直环流弱,且随着k由1℃·km-1逐渐增大,江风环流比陆风环流弱。
当k=β=1℃·km-1,有γ=γm,对应大气层结中性稳定时,江风垂直环流与陆风垂直环流两者仍具有对称性,但其江陆风垂直环流强度比不考虑水汽凝结潜热k=0时的强度大大增强。
2)当0.5℃·km-1≤k≤0.9℃·km-1时,江陆面上方低层出现大风;当k由0.5增大到0.9℃·km-1时,u'由14.3逐渐增大到17.8 m·s-1。特别地,与k=0和其他k值时相比,k=0.9℃·km-1时江陆面上方低层u'极大值绝对值增大3.5 m·s-1,增大24%。
3)与不考虑水汽凝结潜热k=0时江风和陆风垂直环流均有两个环流对不同,k=1.5℃·km-1时,在垂直方向上,江风垂直环流出现三个环流对。而在k=0.9℃·km-1时,在垂直方向上,江风垂直环流出现一个环流对。
4)在整层或低层江陆风环流中心附近流线出现了间断,是由于中心两侧垂直上升和下沉气流对应的水汽凝结加热不同所引起的与锋面类似的间断面。
5)0<k≤β=1℃·km-1时江陆风低层垂直环流比k>β=1℃·km-1时江陆风的环流强得多,而0<k≤β=1℃·km-1时江陆风中上层垂直环流则比0<k<β=1℃·km-1时弱得多。
综上所述,当0<k<β=1℃·km-1,大气层结绝对稳定时,江风垂直环流比陆风环流强,两岸上方上升气流比江面上方上升气流强,两岸比江面容易形成暴雨;而当k>β=1℃·km-1,大气层结条件不稳定时,江风垂直环流比陆风环流弱,江面比两岸容易形成暴雨。当0.5℃·km-1≤k≤0.9℃·km-1时,大气趋近于层结条件不稳定时,江陆面上方低层出现大风。在整层或低层江陆风环流中心附近流线出现了由于水汽凝结加热不同所引起的与锋面类似的间断面,可用于解释天气雷达图显示的海面上空的类似于切变线的线状回波。这一线状回波若与冷锋相遇,则容易形成暴雨。
本文的理论结果可用于分析三峡库区水体对其局地大气垂直环流的影响,对三峡库区暴雨和江面大风形成和发展提供了重要的理论基础,并对其预报提供了改进的线索。关于三峡库区下垫面的改变对库区局地环流的影响需做进一步研究。
黄荣辉,严邦良.1989.一个描述河陆风变化的数值模式及其数值试验[J].大气科学,13(1):11-21.
王浩.1993.深浅水体不同气候效应的初步研究[J].南京大学学报:自然科学,29(3):517-522.
张洪涛,祝昌汉,张强.2004.长江三峡水库气候效应数值模拟[J].长江流域资源与环境,13(2):133-137.
Cho H R,Shepherd T G,Vladimirov V A.1993.Application of the direct Lyaponov method to the problem of symmetric stability in the atmosphere[J].J Atmos Sci,50:822-836.
Defant F.1950.Theorie der land-und seewind[J].Arch Meteor Geophys Bioklimatol,2:404-425.
Estoque M A.1961.A theoretical investigation of the sea breeze[J].Quart J Roy Meteor Soc,87:136-146.
Estoque M A.1962.The sea breeze as a function of the prevailing synoptic situation[J].J Atmos Sci,19:244-250.
Estoque M A.1981.Further studies of a lake breeze,PartⅡ:Theoretical study[J].Mon Wea Rev,100:619-634.
Maddukuri C S.1982.A numerical simulation of an observed lake breeze over southen lake Ontario[J].Boundary-Layer Meteor,22:369-387.
Martin C L,Pielke R A.1983.The adequacy of the hydrostatic assumption in sea breeze modeling over flat terrain[J].J Atmos Sci,40:1472-1481.
McPherson R D.1970.A numerical study of the effect of a coastal irregularity on the sea breeze[J].J Appl Meteor,9:767-777.
Morez W J.1967.A lake breeze on the eastern shore of lake michigan:Observations and model[J].J Atmos Sci,24:337-355.
Ogura Y,Phillips N A.1962.Scale analysis of deep and shallow convection in the atmosphere[J].J Atmos Sci,19:173-179.
Patrinos A N.1977.A numerical study of the Chicago lake breeze[J].Boundary-Layer Meteor,12:93-123.
Pearce R P.1955.The calculation of the sea breeze circulation in terms of the differential heating across the coastline[J].Quart J Roy Meteor Soc,81:351-381.
Pielke R A.1974.A three dimensional numerical model of the sea breeze over South Aflorida[J].Mon Wea Rev,102:115-139.
Shirer H N,Dutton J A.1979.The branching hierarchy of multiple solutions in a model of moist convection[J].J Atmos Sci,36:1705-1721.

