基于模糊自适应速度调节器的异步电机矢量控制系统研究

陈 爽，段国艳,2，王 静，冯华勇

CHEN Shuang1, DUAN Guo-yan1,2, WANG Jing1, FENG Hua-yong1

（1.四川工程职业技术学院，德阳 618000；2.西南交通大学，成都 610031）

0 引言

交流异步电机的数学模型是一个高阶、多变量、强耦合的非线性系统，在相当长一段时间内，其调速性能远不如直流电机，直到引入基于坐标变换的矢量控制算法，才使得交流异步电机调速性能可以和直流电机调速性能相媲美。但是，坐标变换的解耦作用并没有改变异步电机是一个高阶、多变量、非线性系统的本质，基于电机数学模型的矢量控制还是受到电机参数变化的影响。

交流调速系统的根本还是归结于电机的速度控制，目前的控制方式中，大量采用的仍然是传统的PI控制，PI调节器参数的整定方法很多，但大多数都是以对象特性为基础的。为了解决调节器过分依赖于被控对象参数的缺点，在电机的速度控制中引入模糊控制理论，模糊控制具有不依赖于被控对象精确数学模型，便于利用专家经验，适应性、鲁棒性强等特点，能够很好的克服交流调速系统中模型和环境参数的变化。但是单纯的模糊控制又具有存在稳态误差以及稳态时容易抖动的缺点，为了解决此问题，引入模糊控制理论来在线整定PI调节器的参数，这便构成了模糊自适应PI调节器。

1 按转子磁场定向的异步电机矢量控制系统仿真模型

采用参数重构和状态重构的现代控制理论可以实现异步电机定子电流励磁分量和转矩分量之间的解耦，实现了将交流电机的控制过程等效为直流电机的控制过程。依据矢量控制的基本原理建立按转子磁场定向的异步电机矢量控制系统仿真模型，其结构如图1所示。

本系统分为转速控制子系统和磁链控制子系统，其中转速控制子系统与直流调速系统类似采用了串级控制结构。转速控制子系统中设置了转速调节器ASR，转速反馈信号取自于电机轴上的测速传感器。转速调节器的输出Tei作为内环转矩调节器ATR的给定值，转矩反馈信号取自转子磁链观测器，设置转矩闭环的目的是降低或消除两个通道之间的惯性耦合作用。另外，从闭环意义上来说，磁链一旦发生变化，相当于对转矩内环的一种扰动，必将受到转矩闭环的抑制，从而减少或避免磁链突变对转矩的影响。在磁链控制子系统中，设置了磁链调节器AψR，其输入由外部给定，磁链反馈信号来自于磁链观测器。

2 模糊自适应PI调节器

2.1 模糊自适应PI调节器的结构

模糊自适应PI调节器以误差e和误差变化ec作为输入，以比例系数Kp和积分系数Ki或其增量ΔKp、ΔKi作为输出，利用模糊控制规则在线对PI参数进行调整，其结构如图2所示。

2.2 模糊自适应PI调节器的控制规则

模糊自适应PI调节器的作用是为了找出Kp、Ki与e和ec之间的模糊关系，通过不断的检测e和ec，根据模糊控制原理对Kp和Ki进行调整，从而使被控对象具有良好的动、静态性能。从系统的稳定性、响应速度、超调量以及稳态精度等各方面来考虑，Kp、Ki的作用如下：

1）比例系数Kp的作用是加快系统的响应速度，提高系统的调节精度，Kp越大，系统响应速度越快，调节精度越高，但易产生超调。Kp取值过小则会降低调节精度，使得响应速度缓慢，从而延长调节时间。

2）积分系数Ki的作用是消除系统的稳态误差，Ki越大，系统的稳态误差消除越快，但过大的Ki则会在响应的初期产生积分饱和现象，从而引起响应过程的较大超调。Ki过小又会使静态误差难以消除，影响系统的调节精度。

为了和常规PI调节器比较，选择PI调节器参数的增量ΔKp、ΔKi作为模糊调节器的输出。设误差e和误差变化ec，以及ΔKp、ΔKi的模糊子集都是{NB，NM，NS，ZO，PS，PM，PB}， 其中的元素分别代表负大、负中、负小、零、正小、正中、正大，并设模糊子集的论域都为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}。根据实际操作经验和专家知识，建立ΔKp、ΔKi与e、ec之间的模糊规则表，如表1和表2所示。

图1 按转子磁场定向的异步电动机矢量控制系统仿真模型

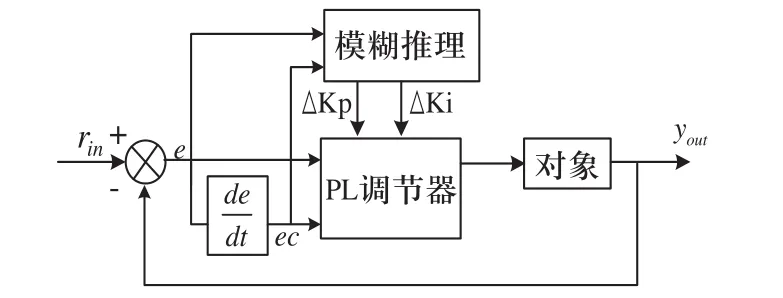
图2 模糊自适应PI调节器结构

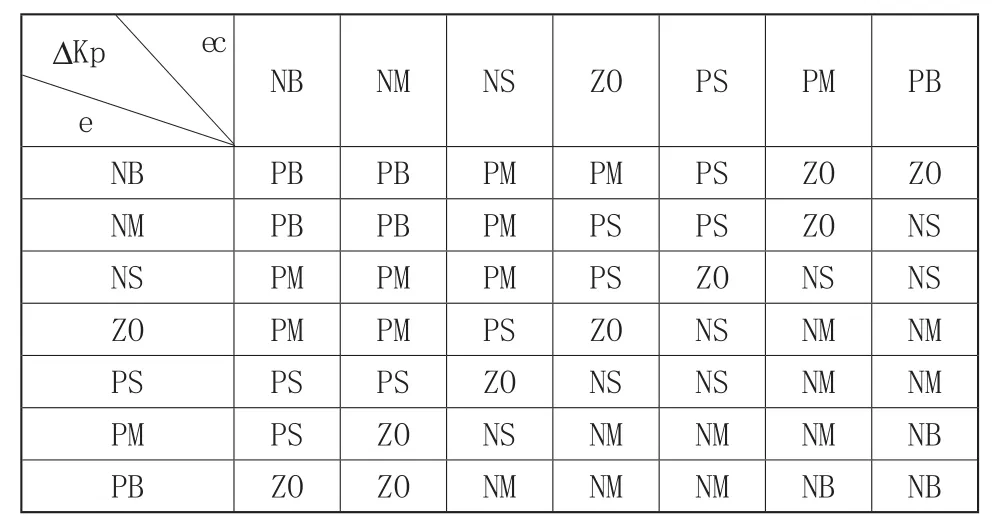
表1 ΔKp的模糊规则表

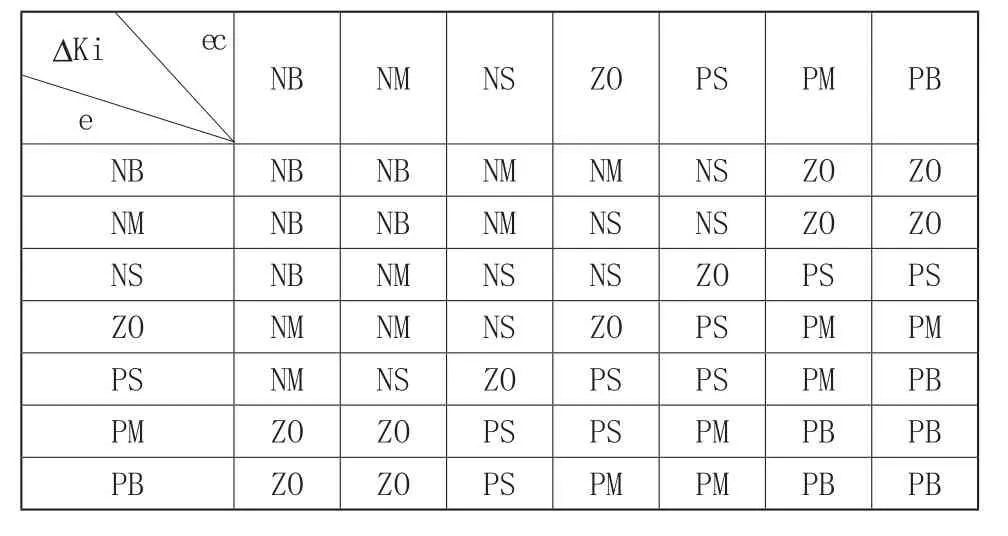
表2 ΔKi的模糊规则表

2.3 量化因子和比例因子的确定

模糊调节器的输入量误差e，误差变化量ec及输出控制量u都是连续变化的精确量，所以先将其离散化。若精确量的实际变化范围为[-x,x]，模糊子集的论域为[-n, n]，则误差的量化因子Ke=n/x，误差变化的量化因子Kc= n/x，输出控制量的比例因子Ku= x/n。

本系统中速度的给定ωr*为100rad/s，控制任务是将电机的速度控制在给定值附近，误差的允许范围为不大于3%，则误差的基本论域为[-3,3]，误差e的量化因子Ke=6/3=2。设误差变化率的允许范围为不大于误差的5%，则误差变化ec的基本论域为[-0.15,0.15]，其量化因子Kec=6/0.15=40。设ΔKp、ΔKi的调整范围为不大于已整定参数的15%，则ΔKp的基本论域为[-0.6，0.6]，其比例因子Kup= 0.6/6=0.1；ΔKi的基本论域为[-6,6]，其比例因子Kui= 6/6=1。

2.4 模糊调节器的建立

MATLAB提供丰富的工具箱，其中就包括用于建立模糊调节器的Fuzzy Logic Toolbox，在MATLAB命令窗口键入fuzzy命令就进入模糊调节器编辑窗口，根据需要建立一个二维的模糊调节器，其输入为e和ec，输出为ΔKp和ΔKi，根据上面的分析分别输入e、ec及ΔKp、ΔKi的量化区间，并选择合适的隶属函数，有三角形、梯形、Z型、S型等多种选择，对结果都没有较大的影响，这里选择对称三角形。根据上面建立的模糊控制规则表，以if…then…的形式输入模糊控制规则。

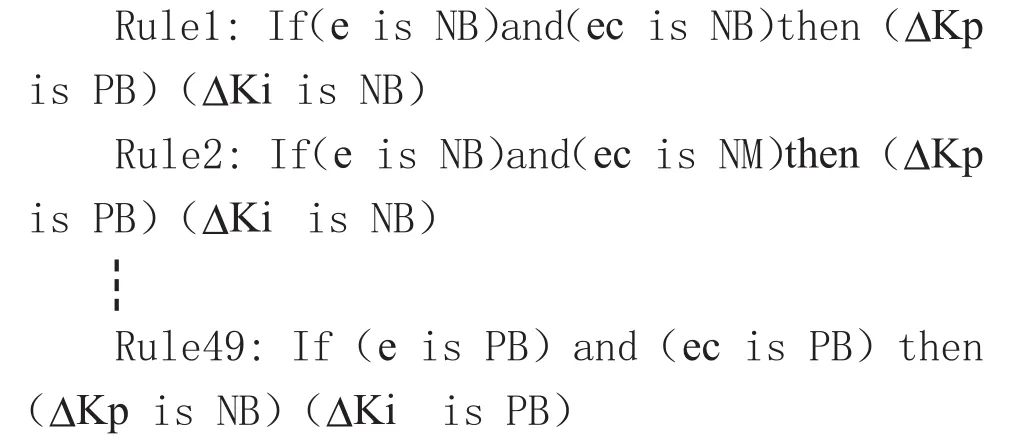
选择调节器的类型为Mamdani，取与（And）的方法为min，或（Or）的方法为max，推理（Implication）的方法为min，合成（Aggregation）的方法为max，解模糊（Defuzzification）的方法为重心法centroid，模糊调节器设计完成以后，保存为safc.fis文件。

3 两种速度调节器的建立和比较

3.1 常规PI速度调节器模型

如图1所示的异步电机矢量控制系统采用常规PI速度调节器，速度给定为100rad/s，通过对速度误差信号的PI调节，输出转矩的给定值。通过反复调整，当速度调节器参数Kp=4，Ki=20的时候，异步电机转速具有良好的动、静态性能。常规PI速度调节器模型如图3所示。

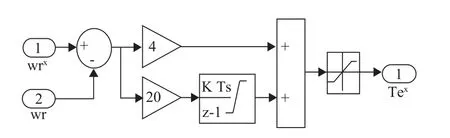
图3 常规PI速度调节器

3.2 模糊自适应PI调节器模型

按照前面的分析，整定后的模糊自适应PI速度调节器参数由下式获得：

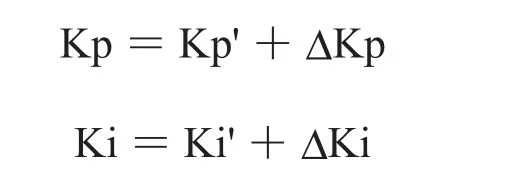
其中，Kp'和Ki为已整定的常规PI调节器参数，Kp、Ki为模糊自适应PI调节器参数，将直接作用于被控对象。在SIMULINK菜单中，选择Fuzzy Logic Toolbox中的Fuzzy logic controller模块并搭建模糊自适应PI速度调节器，如图4所示。

在MATLAB命令窗口输入一条指令matrix=readfis（‘safc.fis’）以获取模糊调节器的信息，双击模糊调节器模块（Fuzzy Logic Controller）并输入matrix，建立模糊调节器和Simulink之间的联系以便运行仿真模型。

4 仿真结果比较

分别采用常规PI速度调节器和模糊自适应PI速度调节器对图1所示的异步电机矢量控制系统进行仿真比较，仿真电机的参数为：Pe=3.7kW，Rs=1.5Ω，Rr=2Ω，Ls=20mH，Lr=30mH，Lm=0.85H，J=0.1kg.m2，np=2，下面给出了相应仿真曲线。图5及图6为给定转速为 =100rad/s时速度和转矩响应曲线。

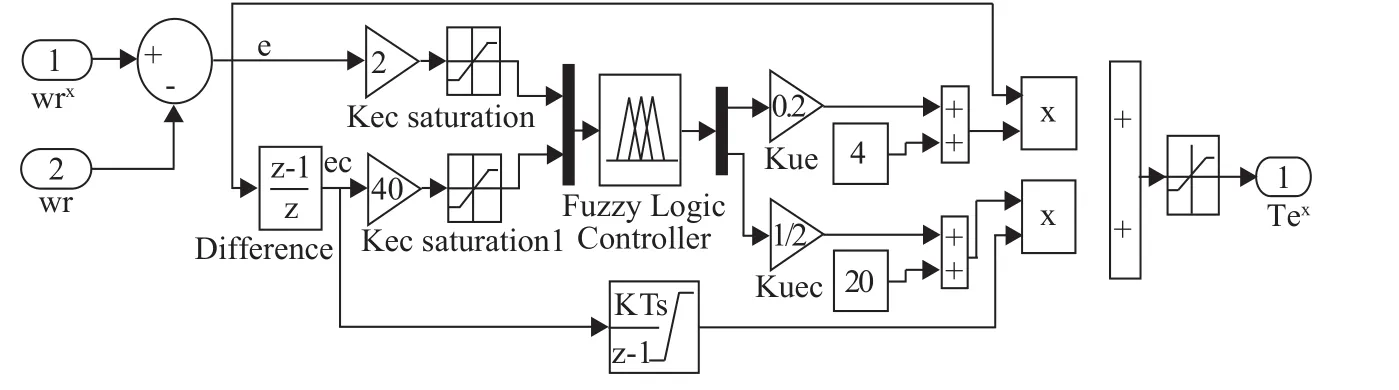
图4 模糊自适应PI速度调节器

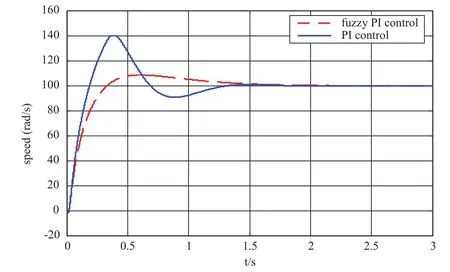
图5 速度响应曲线比较

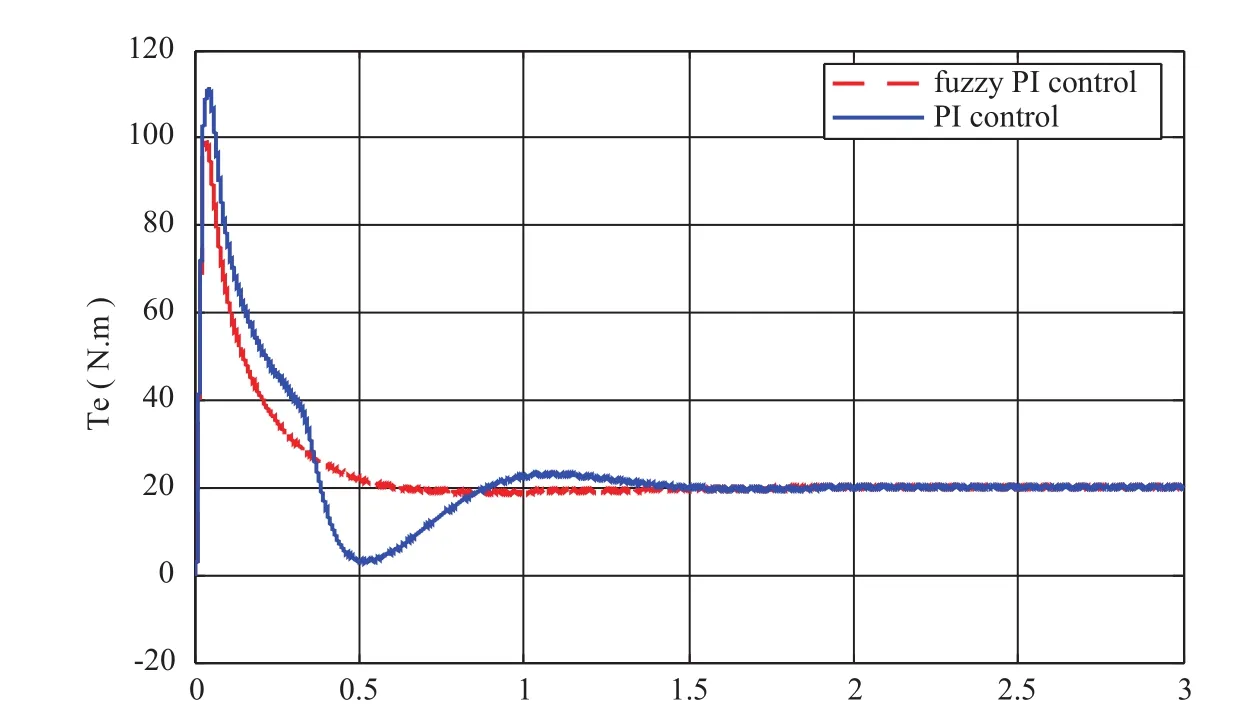
图6 转矩响应曲线比较

5 结论

本文通过整定常规PI速度调节器的参数使系统获得了较好的动静态性能，为了进一步改善系统的响应速度和稳态精度，将模糊自适应PI速度调节器引入异步电机矢量控制系统。仿真结果表明，模糊自适应PI速度调节器增强了系统速度调节的自适应能力，超调量小，响应速度快，大大的改善了系统的动静态性能，具有较高的实用价值。

[1]张静, 等.MATLAB在控制系统中的应用[M].北京∶ 电子工业出版社.2007.

[2]李士勇.模糊控制、神经控制和智能控制论[M].哈尔滨∶ 哈尔滨工业大学出版社.1998.

[3]李华德.交流调速控制系统[M].北京∶ 电子工业出版社.2003.

[4]Rajani K.Mudi, Nikhil R.Pal, A self-tuning fuzzy PI controller, Fuzzy Sets and Systems,2000, 327-338.

[5]M.T.Benchouia, S.E.Zouzou, Modeling and Simulation of Variable Speed Drive System with Adaptive Fuzzy Controller Application to PMSM, IEEE International Conference on industrial Technology, 2004, 683-687.