一种小型电阻应变式三维力传感器的仿真设计

吴 强 俞志伟 吉爱红 戴振东

南京航空航天大学,南京,210016

一种小型电阻应变式三维力传感器的仿真设计

吴 强 俞志伟 吉爱红 戴振东

南京航空航天大学,南京,210016

研制了一种小型电阻应变式三维力传感器,其弹性体由主弹性体和附加弹性体组成,主弹性体上开有若干槽孔,电阻应变片贴于附加弹性体上,而附加弹性体与主弹性体通过物理方式连接。采用有限元方法进行仿真分析,将弹性体的位移变化转变成应变片的应变量,利用静力不同时应变不同的原理分析了弹性体的解耦性能。有限元分析计算和静力实验结果表明,所研制的传感器具有较高的灵敏度,并能够较好地消除各维间的耦合。

电阻应变;力传感器;仿真设计;有限元法

0 引言

传感器在现代科学技术中的重要作用已被人们所充分认识,无论是在工业与国防领域,还是在生物工程、医疗卫生、环境保护等领域,处处都离不开传感器的应用[1]。多维力传感器是实现机器人类人化和智能化最为重要的一种传感器,它是工程力学检测和机器人运动控制的基础,其应用范围也越来越广泛[2-4]。近年来,随着半导体微加工技术的发展,三维力传感器的研究在国外得到了迅速发展,基于不同工作原理的三维力传感器纷纷推出,如压电式[5]、压阻式[6]等,谐振质量块则有单质量块和多质量块等形式[7-8]。在结构上,三维力传感器有悬臂梁型、双梁型、四梁型、岛型、倒T型等形式[9-11]。在实际应用中,有很多场合需要小体积、高灵敏度的三维力传感器,为此,笔者研制了一种新型应变式三维力传感器,该传感器为电阻应变式,采用了一种特殊结构的弹性元件来实现三维力信息的获取。

1 设计原理

电阻应变片是一种能将试件上的应变变化转换成电阻变化的传感元件,其转换原理基于金属电阻丝的电阻应变效应。将应变片贴在被测定物上,使其随着被测定物的应变一起伸缩,这样应变片里面的金属箔材就随着被测定物应变变化而伸长或缩短。应变片就是应用这个原理,通过测量电阻的变化而对应变进行测定。根据电阻应变计测量应变的理论,电阻丝电阻变化率与应变成线性关系[1],即

式中,d R/R为电阻变化率;K为单根金属丝的灵敏系数;ε为金属丝材料的应变值;d L为金属丝长度伸长量,m;L为金属丝的长度,m。

应变片粘贴在受测物件上后,应变值ε随受载变形电阻值将发生相应的变化,使应变片完成由载荷表示的机械量变成电信号的转换。受载后建立载荷与电阻变化量间的函数关系,通过预先确定的载荷标定曲线可获得测量的载荷值。

由式(1)可以发现,物体的应变从几何学角度上看表现为物体上两点间距离的变化。因此可以将弹性元件的尺寸减小到比应变片基底尺寸略大,通过d L的变化得到应变ε,进一步得到被测力。

2 传感器结构设计

传统的只有单一弹性体结构的传感器弹性体尺寸远大于应变片的尺寸,在弹性体设计方面,经常应用“应力集中”的设计原则,以确保贴片部位的应变水平较高,并与被测力保持严格的对应关系,以提高所设计测力传感器的测力灵敏度和测力精度。这样当弹性体尺寸减小时,其应力集中程度急剧下降(例如悬臂梁结构的传感器[12]),从而使贴片部位应变水平大幅下降导致传感器失去实用意义,因此传统的只有单一弹性体结构的传感器尺寸必然远大于应变片尺寸,限制了传感器的使用范围。本文设计了一种新的弹性体结构,使弹性体尺寸减小到与应变片尺寸为同一数量级,满足了小体积测力传感器的使用需求。

弹性体是将外载荷(多维力)转换为应变量的部件,是整个传感器的基础,因此对弹性体的结构形式、材料、几何尺寸(这些因素都对传感器的精度、线性度、灵敏度和稳定性等产生影响)等都需要精心考虑和设计。应变式三维力传感器设计的关键是其结构应在三个方向上对不同方向的力敏感程度不同。本文设计了一种新型的弹性体结构,该传感器由主弹性体、附加弹性体和电阻应变片组成,如图1所示。主弹性体上自上而下开有多层槽孔,上下层槽孔相位相差90°,每个槽孔贯穿长方体的三个面。附加弹性体通过物理方法与传感器主弹性体相连接,起到传递应力的作用,而电阻应变片则贴于附加弹性体上以测量相应的应变。

图1 传感器结构简图

当主弹性体采用实心结构时,由于弹性体整体刚度很高,所以导致贴片部位应变过小而失去实用意义。为了不增大弹性体的尺寸,必须降低弹性体的整体刚度,因此在此弹性体上加工出多层狭窄的槽孔,相邻槽孔之间的相位差是90°,使上下层槽孔间的薄壁区成为应力敏感区。主弹性体每个表面上加工有相同数目的槽孔,与附加弹性体配合,保持了传感器X向和Z向性能的均衡;90°的相位差最大程度保证了不同表面的薄壁区对不同方向的力敏感,从而使传感器在结构上具有了多维力测量能力;槽孔自上而下的螺旋层式布置,可以保证主弹性体在受力时能够产生足够大的轴向位移,通过附加弹性体传递较大的应变,实现Y向力的测量。由于主弹性体开有槽孔,不利于直接粘贴应变片,因此设计了一薄片式的附加弹性体通过物理方法与传感器主弹性体相连接,把应变片粘贴在附加弹性体的外表面上。附加弹性体一方面保证了应变片的整体受力,有利于应变片性能的充分利用,另一方面使粘贴应变片的各个表面的刚度和强度尽可能一致,均衡传感器的各向性能。此外,为了最大程度地利用主弹性体产生的应变,并减小贴片位置精度对传感器灵敏度的影响,在设计弹性体时,尽可能将槽孔开在应变片敏感栅的尺寸范围之内。

该附加弹性体上设计了四个贴片位置A、B、C、D,用于粘贴金属箔式应变片。A贴片和C贴片用于测量X方向的力FX。在力FX的作用下,A贴片和C贴片处产生弯矩,贴于A表面的应变片处于正应力区(拉应力),贴于C表面的应变片处于负应力区(压应力)。由于应变片的压阻效应,上下贴片的阻值会发生变化。阻值变化通过惠斯登电桥的放大作用,使桥路输出电压发生比较大的变化,通过测量电压值变化量就可以得到相应的力值,从而实现力-电转化。同样道理,B贴片和D贴片用于测量Z方向的力FZ。在力FY作用下,四片附加弹性体都受拉力的作用,四片应变片都处于正应力区(拉应力),而在X方向力或Z方向力的作用下,四片应变片总有两片应变方向相反(一正一负),另两片敏感方向与力的方向垂直,由于横向效应带来的应变微小,且理论上整片应变片的应变输出能够正负相抵,因此可认为应变片对Y方向的力不敏感,故可以通过惠斯登电桥的放大作用体现Y向力-电之间的关系。总之,通过连接在主弹性体上的四片电阻应变片可以测量各个面上的变形,进而求得被测力的三个分量(FX,FY,FZ)。

3 模型的有限元分析

3.1 传感器的几何建模

有限元分析软件ANSYS是传感器仿真设计中的强大工具,在应变分析和固有频率求取方面具有高度可信的仿真结果[13-15]。弹性体材料和结构参数不同,传感器的灵敏度和固有频率就不同。根据实际应用的需要,笔者选用硬铝合金为主弹性体材料,酚醛树脂片为附加弹性体,两者通过物理粘贴方式相连。主弹性体的尺寸为10.0mm×10.0mm×16.0mm,应变片选用中航电测仪器厂生产的BE350-10A,其敏感栅尺寸为10.0mm×4.8mm,基底尺寸为13.8mm×6.6mm。

3.2 弹性体应变计算

在有限元分析中,根据传感器安装固定的方式在主弹性体底面施加面约束,分别在长方体顶部端面中心施加满量程集中力载荷,受力的坐标轴如图1所示。

为了求得式(1)中的d L,即应变片敏感栅长度方向上距离的变化,在ANSYS中采用位移在Y方向上的投影进行求解,分别求出受力后应变片敏感栅上下边界的Y坐标,两者相减即为d L。由于应变片敏感栅具有一定的宽度,不同宽度处的应变值不同,因此不能使用一条线上的d L代表整片应变片的轴向变形。为了使求得的d L能代表整个应变片敏感栅的变形量,我们使用平均变形量代表一片应变片的d L。我们将敏感栅总体宽度分为20份,相当于使用21条线的平均变形量代表一片应变片的d L,然后根据式(1)求得应变ε。求d L的具体方法如下:首先采用ANSYS的路径映射技术将位移结果映射到选定的路径上(应变片敏感栅上下边界),每条路径默认分为20份,即将4.8mm均分为20份,共标记为21点,得到每个点上的坐标,然后由下式求得贴片的变形量d L:

式中,yai为应变片敏感栅上边界第i个标记点的Y坐标;ybi为应变片敏感栅下边界对应上边界第i个标记点的Y坐标。

当X方向受力时,应变片A受到压应力,金属丝长度变短,d L为负值;应变片C受到拉应力,金属丝长度变长,d L为正值;而应变片B和D理论上半边受拉,半边受压,对整片应变片而言,拉压引起的金属丝长度变化互相抵消,输出电阻不变,d L接近零值。应变片金属丝长度方向与弹性体高度方向一致,顶端受力,应变片敏感栅上边界位移远大于应变片敏感栅下边界位移。在ANSYS中利用路径映射可以方便地求得4片应变片敏感栅上边界的位移分布,如图2所示。同理也可求得下边界的位移分布。由图2可见,X方向受力时A片和C片位移较大且分布较均匀,B片和D片位移较小且沿敏感栅中线反向对称。

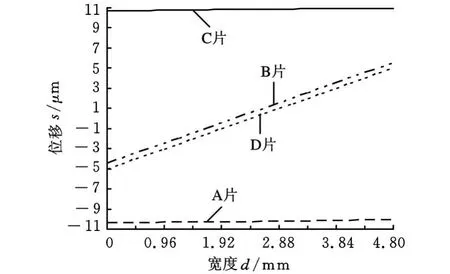
图2 应变片A、B、C、D上边界位移分布

3.3 传感器有限元分析结果

用上述数据处理方法,分别在X、Y、Z方向上施加大小为5N的力,可以得到各个应变片上的输出结果,见表1。

表1 四个应变片的应变量

通过结构静力分析可以发现,X方向的力主要影响A应变片和C应变片,一片受拉,一片受压,对B和D位置不敏感;Z方向的力主要影响B应变片和D应变片,一片受拉,一片受压,对A和C位置不敏感;Y方向的力同时影响A、B、C、D应变片,对四片应变片均敏感,四片应变片同时受拉或受压。因此我们可以用A应变片和C应变片应变之差作为一路信号εX,标记为力FX;B应变片和D应变片应变之差作为一路信号εZ,标记为力FZ;A、B、C应变片和D应变片应变之和作为一路信号εY,标记为力FY。这与理论分析一致,可以设定传感器共有三组桥路输出。

利用ANSYS的模态分析功能,获得该三维传感器的前三阶固有频率分别为2512.5H z、2579.4H z、5823.4H z,其振型分别为沿 X 、Z 、Y 方向的平动。根据其一阶固有频率的2/3来确定该传感器的工作频率带宽为0～1675H z。

4 解耦分析

基于电阻应变测量的多维力传感器的弹性体结构最理想的情况是,弹性体结构在贴片位置的应变变化通过应变片桥路的转化后所得到的电信号只对被测力的某一个分量敏感,不受其他方向力的影响。但是传感器的弹性体作为一个物理实体,它受到的任何方向的力都会在弹性体的各个位置有所体现,只是表现程度不同而已,因此桥路的输出信号出现维间数据耦合的情况是不可避免的。

维间耦合使多维传感器的性能指标受到明显的影响。要消除或抑制耦合,有两条路径:一是设法消除其产生的根源,这涉及传感器的结构形式和制造工艺等诸多问题,往往难以解决,同时又会增加传感器的制造成本;二是利用标定矩阵,采取模拟或数字信号处理方法消除维间耦合,这种方法既能降低对传感器制造工艺的要求,又能获取较准确的测量结果。

由于该多维力传感器采用了一个结构独特、构造复杂的弹性元件,通过桥路输出搭配实现多维力的测量,所以在设计传感器时,要保证桥路的输出信号能解耦,否则传感器将无法正常工作。为了在设计阶段保证传感器具有良好的解耦性,我们使用ANSYS软件分析弹性体是否能解耦。

从传感器设计原理上讲,若X、Y、Z三方向输出互不影响,则桥路输出应变ε与力的关系为

而实际上三维输出并不一定是完全独立的,而是互相影响、维间耦合的。桥路输出应变ε与力的关系应该为

其中,应变ε为输出应变向量,C为解耦矩阵,F为负载力向量。解耦矩阵C可以通过标定获得,其元素CXY的物理意义为:在Y方向施加单位载荷力时,X方向上的电压输出值。因此,需要轮换在X、Y、Z方向上施加一组已知的定值载荷。每次加载时都必须求出三个桥路的输出应变ε。根据ANSYS求出的输出应变ε获得九条传感器桥路特性曲线(X、Y、Z方向分别加载时,三组桥路输出的应变ε特性曲线),将特性曲线通过最小二乘法拟合成一条直线,将直线方程转化为y=kx+b的形式。该直线的斜率k对应解耦矩阵中九个系数中的一个。

对某个采用主弹性体和附加弹性体结构的传感器,使用有限元软件进行仿真分析,若在X方向分别施加一组大小不等的定值力(0、2、3、5)N,在ANSYS中可分别求出相应的位移,计算结果如表2所示。

表2 X方向定值力下的输出应变

根据最小二乘法拟合成三条直线,即为FX方向输出应变特性曲线,三条直线的斜率分别对应 CXX 、CY X 、CZX,如图 3所示。

图3 FX方向标定结果曲线

由图3可得,CXX=443.094,CYX=131.597,CZX=11.178。同理可得FY方向和FZ方向输出应变特性曲线,获得解耦矩阵的相关系数。

根据最小二乘法拟合直线求得解耦矩阵的系数的方法,可以获得解耦矩阵C:

根据式(6),已知弹性体的受力可以求得桥路输出应变。反之,已知桥路输出应变也可求得施加在弹性体上的力,即

采用最小二乘法拟合直线这种做法的前提是假定弹性体在任意一个方向上受力时位移都是线性变化的,为了验证这一假设的正确性,下面进行反算验证。

分别任取两组数据,一组FX=-1N、FY=-2N 、FZ=-4N,一组 FX=-2N 、FY=-3N 、FZ=-3.5N,一种做法是在ANSYS中分别求出两组力下弹性体的应变输出,另一种做法是将两组力分别代入式(6),求出桥路的应变输出。两种做法得出的结果如表3所示。

表3 力与桥路输出关系验证

比较两种方法的结果可以看出,两个结果极其接近,这一方面说明线性位移的假设是正确的,另一方面也说明了弹性体具有良好的解耦性,即可依据式(7)由测得的桥路应变输出求得施加在弹性体上的力。

5 传感器静态标定

在标定实验设计中,根据力传感器的特点和现有实验条件,把重力作为静态标定的标准量。重力具有获取容易、数值恒定、方向性好等优点。具体做法是,先逐级给传感器输入一个标准载荷(砝码),再将载荷逐级减小到零,将每个载荷下传感器的输出记录下来,得到传感器的标定曲线。图4所示为X轴标定曲线,纵坐标值反应应变的程度,横坐标值是重力的大小,同理可得到其他方向的标定曲线。由标定结果可知,传感器存在维间耦合,因此有必要利用标定矩阵消除维间耦合,提高传感器测量结果的准确性。

图4 X轴标定曲线

根据标定曲线计算可知:X轴的直线度为1.1%,在Y方向和Z方向上产生的干扰输出很小,最大干扰误差小于5.5%。同理,Z轴的直线度为0.7%,在X方向和Y方向上产生的干扰输出也很小,最大干扰误差小于5.0%。而Y轴受四片应变片的综合影响,直线度为9.6%,在X方向和Z方向上产生的干扰输出较大,最大干扰误差小于15.2%。

6 结构参数对传感器性能的影响

采用主弹性体和附加弹性体结构的传感器,影响其灵敏度和固有频率的结构因素主要有槽孔数量、槽孔大小、孔间薄壁的高度、附加弹性体的材料和厚度等,这些参数中的任何一个都能改变传递到应变片上的应变和传感器的强度和刚度,影响传感器的性能。

在外形尺寸参数不变的情况下(图1),主弹性体上的槽孔横向深度可以有不同的量值,例如6mm 、7mm 、8mm、9mm 等。在有限元中可以考察不同槽孔横向深度对传感器性能的影响,为了便于比较,每个方向上的力均取为5N,仿真分析结果如表4所示。

表4 槽孔深度对传感器性能的影响

由表4可以看出,随着槽孔横向深度的增加,输出应变随之增大,而固有频率随之减小,这是因为槽孔横向深度越大,对弹性体刚度和强度破环越严重。综合对比各组数据可以发现,X向输出应变和Z向输出应变明显大于Y向输出应变,这是因为X向和Z向具有明显的悬臂梁特征,而Y向的悬臂梁特征不明显,故Y向刚度明显大于X向和Z向刚度,导致应变输出较小。

传感器的结构参数决定了传感器的性能,因此可以通过修改结构参数来满足传感器不同量程、灵敏度以及固有频率等性能指标的要求。

7 结论

(1)设计了一种新型的电阻应变式传感器,该传感器采用主弹性体和附加弹性体的特殊结构,有效减小了传感器的体积,结合适当的电桥组桥方式实现了三维力的测量。

(2)采用有限元仿真解耦分析法,能准确判断复杂结构传感器的解耦性。但是需要注意的是,有限元仿真解耦分析法得到的解耦矩阵不能代替传感器的静态标定矩阵,实际传感器由于其制造误差、贴片误差及电路等的影响,其静态标定矩阵不同于耦合分析中的解耦矩阵C。

(3)提出的新的弹性元件结构设计方法能在同样的测量条件下提高传感器的灵敏度,同时还可以按照测量需要修改弹性元件参数,方便地改变传感器的灵敏度。可以选择传感器各轴向灵敏度及其一致性和固有频率等设计目标进行结构尺寸优化,进一步提高传感器性能,满足不同的使用要求。

[1] 孟立凡,郑宾.传感器原理及技术[M].北京:国防工业出版社,2005.

[2] 徐斌,秦岚,刘俊,等.新型压电式三维力传感器的设计及特性研究[J].国外电子测量技术,2009,28(7):40-44.

[3] Joo JW,Na K S,Kang D I,etal.Design and Evaluation of a Six-com ponent Load Cell[J].Measurement,2002,32:125-133.

[4] Chao Luping,Yin C Y.The Six-component Force Sensor for Measuring the Loading of the Feet in Locomotion[J].Materials and Design,1999,20:237-244.

[5] 张军,李寒光,李映君,等.压电式轴上六维力传感器的研制[J].仪器仪表学报,2010,31(1):73-77.

[6] 姜彤,王世清,韩伟.机械手三维力传感器的设计[J].传感器世界,2005(8):10-12.

[7] Takao H,Matsumo lo Y,Seo H,et a l.Analysis and Design Considerations of Three Dimensional Vector A ccelerometer Sing SIO Structure for H igh Temperature Range[J].Sensors and Actuators,1996,55(8):91-99.

[8] Seidel H,Riedel H,Ko lbeck R,et al.Capacitive Silicon Accelerometer w ith H ighly Symmetrical Design[J].Sensors and A ctuators,1990,49(21):312-315.

[9] 张新,费业泰.应变式全剪切三维加速度传感器的设计[J].中国机械工程,2007,18(10):1157-1160.

[10] 张正杰,吉爱红,王周义,等.用于壁虎脚掌接触力测试的3-维传感器[J].传感技术学报,2007,20(6):1271-1274.

[11] Phan JV,Hocken R,Sm ith S T,et al.Simu ltaneous Measurement of Spatially Separated Forces Using a Dual-cantilever Resonance-based Touch Sensor[J].Review o f Scientific Instruments,2002,73(2):318-322.

[12] 吴强,吉爱红,王周义,等.一种测力传感器固有频率的提高与测试[J].传感技术学报,2010,23(2):235-238.

[13] 赵建才.拉-压力传感器线性度的有限元分析[J].传感器技术,2001,20(12):24-28.

[14] 张怀亮.压力传感器线性度的有限元分析[J].中南大学学报(自然科学版),2004,35(3):429-433.

[15] 章焕文.用有限元法预估框架固有频率[J].航空精密制造技术,1995,31(6):28-32.

Development of a Miniature Resistance Strain Three Dimensional Force Sensor

Wu Qiang Yu Zhiw ei Ji Aihong Dai Zhendong
Nan jing University of Aeronautics and A stronautics,Nanjing,210016

The paper developed aminiature three dim ensions force sensor of resistance strain type.It used strain gauge as sensing element for the detection o f force.The elastomers were composed with central and additional elastomers.Central elastomer having some cutting slots w as joined physically with additionalelastomer adhering to resistance strain.The displacement variables ofelastomerswere translated into dependent variable of strain type.Itwas analyzed based on different decoupling capabilities of the elastomers under different static forces by ANSYS simulator.Experimental resultshave indicated three dimensional force sensor has desirable sensitivity and can remove coup ling in different dimensions.

resistance strain;force sensor;simulation design;finite elementmethod

TP212.12

1004—132X(2011)11—1288—06

2010—06—28

国家高技术研究发展计划(863计划)资助项目(2007ZA 04Z201);中国博士后科学基金资助项目(20100471339);南京航空航天大学基本科研业务费专项科研项目(NS2010223);南京航空航天大学引进人才科研启动基金资助项目(S0913-GXY)

(编辑 王艳丽)

吴 强,男,1984年生。南京航空航天大学机电学院硕士研究生。主要研究方向为多维测力传感器设计及力学测试、生物运动力学。俞志伟,男,1980年生。南京航空航天大学高新技术研究院讲师。吉爱红,男,1973年生。南京航空航天大学高新技术研究院副教授。戴振东,男,1962年生。南京航空航天大学高新技术研究院教授。