滚珠丝杠副非协调性接触特性研究

王福吉 阳江源 贾振元 王 威 卢晓红

大连理工大学精密与特种加工教育部重点实验室，大连，116024

滚珠丝杠副非协调性接触特性研究

王福吉 阳江源 贾振元 王 威 卢晓红

大连理工大学精密与特种加工教育部重点实验室，大连，116024

滚珠丝杠副中滚珠与丝杠滚道和螺母滚道的接触是一种典型的非协调性接触，这种接触的特性对滚珠丝杠副的承载能力、传动效率和定位精度等都有着重要的影响。为此，采用Hertz接触理论建立了滚珠丝杠副轴向接触刚度的求解公式，然后从滚珠丝杠副轴向负载、设计参数和材料属性等方面分析了滚珠丝杠副的接触特性，最后运用有限元分析软件ANSYS对滚珠与丝杠滚道的接触进行仿真，仿真结果与理论结果非常相近，从而验证了理论分析的正确性。研究结果为高速、重载和精密滚珠丝杠副的设计与使用提供了理论指导。

滚珠丝杠副；非协调性接触；轴向接触刚度；有限元仿真

0 引言

滚珠丝杠副是数控机床及加工中心中实现精密传动和定位的关键功能部件，由丝杠、螺母、滚珠和循环反向机构组成，通过滚珠在丝杠滚道与螺母滚道之间做点接触的滚动来实现丝杠或螺母的位移。滚珠与丝杠滚道、螺母滚道的接触特性对滚珠丝杠副的承载能力、传动效率、定位精度和重复定位精度都有着重要影响，因此，研究滚珠丝杠副的接触特性可为提高滚珠丝杠副的传动效率和工作性能提供理论依据。Chen等［1］利用光弹性效应和电子图像处理技术提出了一种测量滚珠丝杠接触角的新方法，提高了接触角的测量效率。Mei等［2］通过分析滚珠丝杠副的负载分布对滚珠与滚道的接触情况的影响，得出了滚珠丝杠副接触位置误差会造成滚珠Hertz接触负载改变的结论。杜平安［3］对大螺旋升角滚珠直旋副的滚道弹性变形与额定静载荷之间的关系进行了研究。姜洪奎等［4］在考虑螺旋升角的影响下，应用微分几何理论推导了滚珠丝杠螺旋面的主曲率，进而分析了螺旋升角对滚珠丝杠副弹性变形的影响。这些工作考虑了负载、摩擦和螺旋升角等对丝杠性能的影响，丰富了研究内容，为建立准确的滚珠丝杠副接触模型提供了理论依据。但以上研究都没有对滚珠丝杠副的接触特性进行系统分析，没有对滚珠丝杠副的接触刚度进行理论推导。

本文将滚珠与滚珠丝杠滚道、滚珠螺母滚道的接触视为非协调性接触［5］，根据Hertz接触理论对滚珠丝杠副的接触特性进行了理论推导，建立了滚珠丝杠副轴向接触刚度的求解公式，进而分析了滚珠丝杠副的设计参数及材料属性与接触特性的关系，最后应用ANSYS仿真分析软件对滚珠丝杠副接触变形进行了验证。

1 滚珠丝杠副的接触刚度计算

理想状况下，认为滚珠丝杠副内的每个工作滚珠承受的负载都是相同的。假设滚珠丝杠副每个承载滚珠的法向载荷为P，承载滚珠数为Z，滚珠与丝杠滚道及螺母滚道的接触角为β，滚珠丝杠副的螺旋升角为λ，由于滚珠所受摩擦力相对于其所受的法向载荷很小，可以忽略，因此所有承载滚珠的法向载荷与滚珠丝杠副的轴向负载F之间的关系为［6］

根据非协调性Hertz接触理论，两点接触物体的法向载荷P与相应的法向接触变形δn（下标n表示滚珠与螺母接触）之间的关系如下［7］：

以滚珠为受力分析对象，取其中心为坐标原点，Z轴平行于丝杠轴线，在不考虑重力影响的条件下，滚珠的受力如图1所示。根据变形协调条件可知，由法向接触变形量δn引起的滚珠丝杠副轴向变形量δa为

图1 滚珠受力示意图

根据上述数学模型，求得滚珠丝杠副轴向接触刚度为

由式（19）可知，滚珠丝杠副的轴向接触刚度受到负载、设计参数和制造材料属性等多方面的影响，对这些影响因素进行分析可为滚珠丝杠副的结构优化设计提供理论依据。

2 滚珠丝杠副接触特性影响因素分析

2.1 滚珠丝杠副轴向负载的影响分析

滚珠丝杠副的轴向承载能力直接影响滚珠丝杠副的额定动载荷和静载荷，是滚珠丝杠副设计中的一个重要参数。

由式（19）可以看出，接触刚度是滚珠丝杠副的轴向负载的幂函数，负载大时接触刚度大，负载小时接触刚度小，若负载为零，则接触刚度也不再存在。以某厂生产的4016型高速滚珠丝杠副为例（其参数如表1所示），其轴向负载与接触刚度的关系曲线如图2所示。

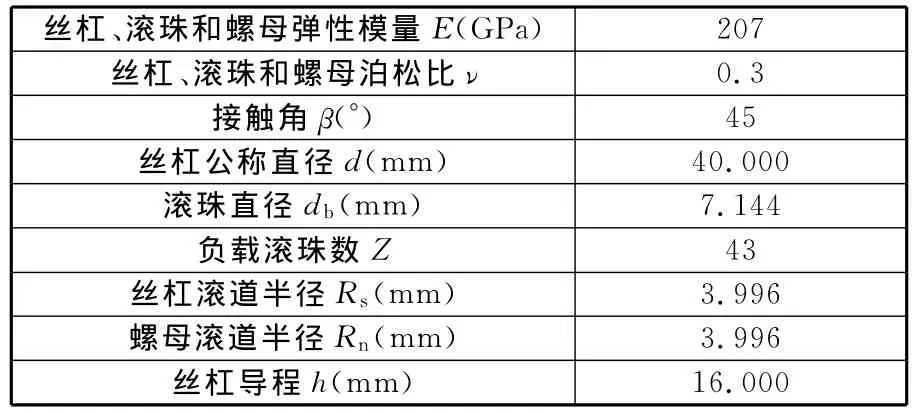
表1 4016高速滚珠丝杠副设计参数

图2 滚珠丝杠副轴向负载与轴向接触刚度关系曲线

2.2 滚珠丝杠副设计参数的影响分析

2.2.1 丝杠导程的影响

高速切削加工需求的增长促进了滚珠丝杠副进给速度的提高。提高滚珠丝杠副进给速度的一个重要方法是加大滚珠丝杠副的导程，从而在同样的电机旋转速度下，伺服电机每转一圈的行程变长。滚珠丝杠的公称直径不变时，导程增大也就是螺旋升角变大。设滚珠丝杠副的轴向负载为10k N，其他参数如表1所示，丝杠导程从5mm增加到32mm时相应的滚珠丝杠副轴向接触刚度变化如图3所示。

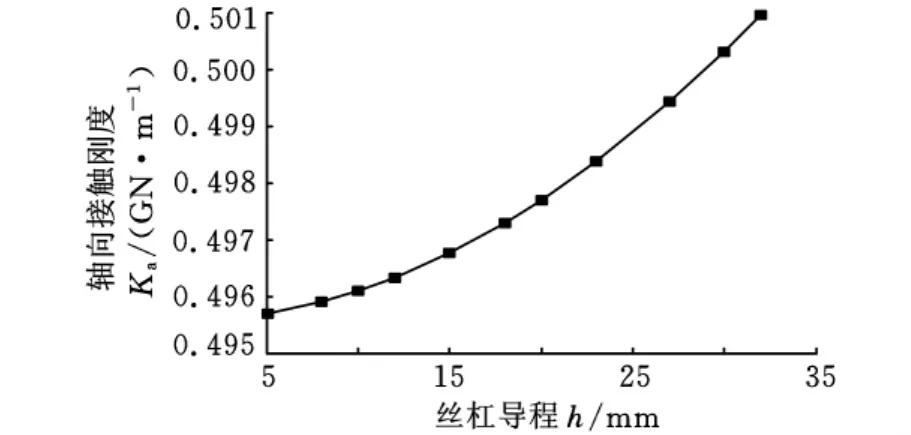
图3 丝杠导程与滚珠丝杠副轴向接触刚度关系曲线

2.2.2 接触角的影响

为分析滚珠丝杠副接触角对轴向接触刚度的影响，设丝杠轴向负载为10k N，接触角从10°变化至90°，其他参数如表1所示，得到接触角与轴向接触刚度关系曲线如图4所示。

图4中轴向接触刚度随着接触角的变大而增大，呈非线性关系。适当增大接触角能够提高滚珠丝杠副的接触刚度，从而减小因轴向负载增大而产生的弹性变形，进而提高定位精度。

2.2.3 负载滚珠数的影响

图4 接触角与滚珠丝杠副轴向接触刚度关系曲线

负载滚珠数与丝杠轴向接触刚度关系曲线如图5所示。可以看出，负载滚珠数越多，滚珠丝杠副的轴向接触刚度就越大，即增加负载滚珠数能够提高滚珠丝杠副的承载能力。然而实际生产中由于制造滚珠时并不能保证滚珠的大小完全一致，而且丝杠滚道、螺母滚道的制造都有一定的偏差，并不能保证每个滚珠都能和丝杠滚道、螺母滚道完全接触，因而滚珠数目增加到一定程度后再增加滚珠个数就不一定能提高滚珠丝杠副的轴向接触刚度了。

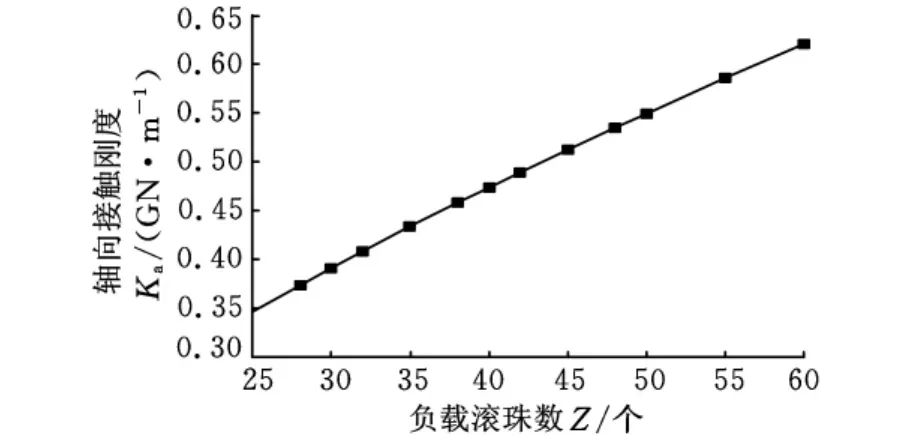
图5 负载滚珠数与滚珠丝杠副轴向接触刚度关系曲线

2.3 滚珠丝杠副制造材料属性对接触刚度的影响分析

由理论推导可知，滚珠丝杠副的制造材料对轴向接触刚度的影响是通过材料的弹性模量E和泊松比ν的变化而体现的［8］，因此，下面分别对其进行分析。

2.3.1 弹性模量的影响

设丝杠轴向负载为10k N，制造材料的弹性模量选择从50GPa至350GPa不等，其他参数如表1所示，得到弹性模量对滚珠丝杠副轴向接触刚度的影响如图6所示。

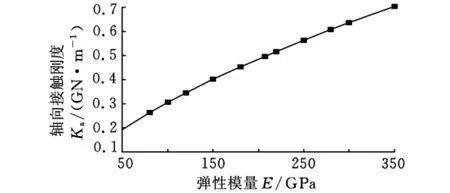
图6 弹性模量与轴向接触刚度关系曲线

可以看出，滚珠丝杠副的轴向接触刚度随弹性模量的增加呈明显非线性增大趋势。

2.3.2 泊松比的影响

在保持其他条件不变的情况下，若泊松比从0.1增加到0.4，相应滚珠丝杠副轴向接触刚度的变化曲线如图7所示，呈现幂函数形式。当泊松比小于0.2时，轴向接触刚度的变化较为平缓；当泊松比大于0.2时，轴向接触刚度随泊松比的增大迅速增大。

图7 泊松比与轴向接触刚度关系曲线

2.3.3 材料属性的综合影响

实际应用中，一旦确定了滚珠丝杠副的材料，相应的弹性模量和泊松比也就随之确定。为了满足实际应用需要，有必要考虑材料属性的综合影响。

滚珠丝杠副的传统制造材料为轴承钢。近年来，为了适应滚珠丝杠副高进给速度的要求，滚珠丝杠副大多采用Si3N4陶瓷材料。分别取全钢式（滚珠丝杠、滚珠螺母和滚珠全部采用轴承钢制造）、混合式（滚珠丝杠和滚珠螺母采用轴承钢制造，滚珠采用Si3N4陶瓷材料制造）和陶瓷式（滚珠丝杠、滚珠螺母和滚珠全部采用Si3N4陶瓷材料制造）三种滚珠丝杠副，计算它们在不同负载下的轴向接触刚度，如图8所示。

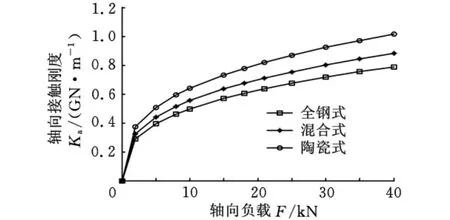
图8 不同材料的丝杠负载与轴向接触刚度关系曲线

可以看出，任一相同丝杠轴向负载下的三种材料的接触刚度存在如下关系：全钢式的接触刚度小于混合式的接触刚度，而混合式的接触刚度又小于同样情况下的陶瓷式的接触刚度。可见在滚珠丝杠副中应用新型陶瓷材料，不仅有利于提高进给速度，而且可以提高滚珠丝杠副的轴向接触刚度和轴向定位精度。

3 滚珠与丝杠滚道接触变形的仿真

为验证前述理论推导过程的正确性，利用三维绘图软件Pro／E建立了滚珠与丝杠滚道相互接触的模型，如图9所示。

图9 滚珠与丝杠滚道接触模型

由于滚珠丝杠副接触的对称性，适当简化后导入ANSYS建立的有限元模型如图10所示。选择Solid92单元作为基本单元格，因为这种单元能够很好地适应接触力的计算，同时对网格的自由划分和接触对的创建有很大的帮助。滚珠与丝杠滚道的接触对选用TARGE170和CONTA174单元格，滚珠与丝杠间静摩擦因数选为0.2，刚度矩阵种类为Unsymmetric，接触初始调节量为0.1，最后施加自由度约束及载荷。

图10 滚珠与丝杠滚道接触分析的有限元模型

设丝杠轴向负载为10k N，4016型滚珠丝杠副接触角为45°，由式（1）和式（15）可知，每个滚珠法向压力P＝331.54N，法向变形为7.162μm。

由有限元仿真得到的结果如图11所示。可以看出，滚珠与丝杠滚道接触变形的最大值为6.957μm，与Hertz接触理论计算出的理论值仅相差2.86%。考虑到Hertz接触理论是基于接触面绝对光滑的条件建立的，即忽略了摩擦力对接触变形的影响，而实际接触时往往伴随有塑性变形，因此，可以初步认为本文基于Hertz理论建立的滚珠丝杠副接触模型是正确的。

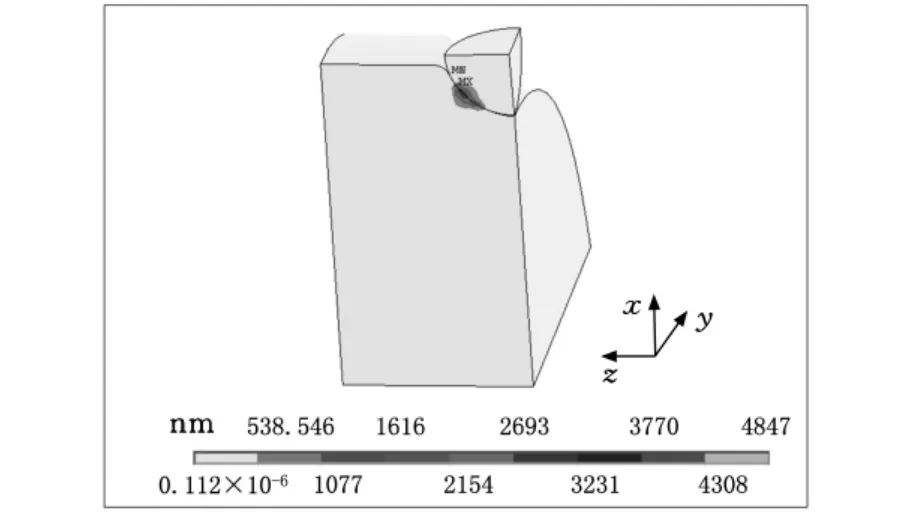
图11 滚珠与丝杠滚道接触变形图

4 结论

研究滚珠丝杠副的接触特性可为提高滚珠丝杠副的传动效率和工作性能提供理论依据。本文根据非协调性Hertz接触理论建立了滚珠丝杠副的轴向接触刚度模型，并对接触刚度的影响因素（负载、设计参数和制造材料属性等）进行了分析，获得了各影响因素对接触刚度的影响曲线。最后，应用ANSYS仿真对滚珠与丝杠滚道的接触变形进行了仿真，仿真结果与理论计算结果相近，从接触变形的角度验证了所建立的滚珠丝杠副接触刚度模型的正确性。

［1］Chen T Y，Hou P H，Chiu J Y.Measurement of the Ballscrew Contact Angle by Using the Photoelastic Effect and Image Processing［J］.Optics and Lasers in Engineering，2002，38：87－95.

［2］Mei Xuesong，Masaomi Tsutsumi，Tao Tao，et al.Study on the Load Distribution of Ball Screws with Errors［J］.Mechanism and Machine Theory，2003，38：1257－1269.

［3］杜平安.滚珠直旋副滚道弹性接触分析［J］.电子科技大学学报，1994，23（3）：280－285.

［4］姜洪奎，宋现春，张佐营.螺旋升角对滚珠丝杠副弹性变形的影响分析［J］.中国机械工程，2008，19（9）：1079－1083.

［5］Paul B，Hashemi J.Contact Pressures on Closely Conforming Elastic Bodies［J］.ASME Journal of Applied Mechanics，1981，48：543－548.

［6］程光仁，施祖康，张超鹏.滚珠螺旋传动设计基础［M］.北京：机械工业出版社，1987.

［7］Johnson K L.Contact Mechanics［M］.Cambridge：Cambridge University Press，1985.

［8］Antoine J F，Visa C，Sauvey C，et al.Approximate Analytical Model for Hertizian Elliptical Contact Problems［J］.ASME Journal of Tribology，2006，128：660－664.

Study on Non－conformal Contact Characteristics of Ball Screw

Wang Fuji Yang Jiangyuan Jia Zhenyuan Wang Wei Lu Xiaohong
Key Laboratory for Precision and Non－traditional Machining Technology of the Ministry of Education，Dalian University of Technology，Dalian，Liaoning，116024

The contact between balls and screw races or nut races is a kind of typical non－conformal contact and its characteristics will influence greatly on ball screw’s load capacity，transmission efficiency and positioning accuracy.Thus Hertz contact theory was adopted to construct the solution formula of ball screw’s contact stiffness，then ball screw’s contact characteristics in terms of axial load，design parameters and material properties were analyzed，and the contact deformation values of the contact between balls and screw races were obtained through finite element simulation method.The simulation results are close to the theoretic ones，which proves the correctness of the theoretic analyses.The present study offers theoretical support for the design and application of high speed，heavy load and precision ball screws.

ball screw；non－conformal contact；axial contact stiffness；finite element simulation

TH132.1

1004—132X（2011）19—2293—05

2010—09—26

国家科技重大专项（2009ZX04011－033）；辽宁省教育厅科研项目（LT2010020）

（编辑 陈 勇）

王福吉，男，1974年生。大连理工大学机械工程学院副教授、博士。研究方向为精密加工与特种加工、精密测控和微执行器的研制等。阳江源，男，1986年生。大连理工大学机械工程学院硕士研究生。贾振元，男，1963年生。大连理工大学机械工程与材料能源学部部长、教授、博士研究生导师。王 威，男，1986年生。大连理工大学机械工程学院硕士研究生。卢晓红，女，1979年生。大连理工大学机械工程学院讲师。