滤波法控制混沌的电路实验

安 迪，高媛媛，姜凤怡

（1．吉林大学 电子科学与工程学院，吉林 长春130012；2．东北师范大学 物理学院，吉林 长春130024）

1 引 言

混沌控制是混沌领域的热点课题之一［1－3］．控制混沌的方法有很多，但大体上分为反馈控制和非反馈控制两大类．反馈控制方法的基本思想是：将系统输出信号直接或通过某种组合或变换后送给系统本身，利用反馈信号的调制或控制作用使得系统的运动状态从混沌态转变成周期态或不动点，如延迟反馈控制法、线性反馈控制法、凹槽滤波反馈控制法等．

越来越多的院校已将混沌理论与实验引入到大学物理教学中［4－7］．本文基于反馈控制机理，提出利用低通滤波器控制混沌的方法，即将混沌系统的输出信号经过低通滤波后回送给系统，利用低通滤波器的相移特性，适当调节电路元件参数，可达到控制混沌的目的．该方法电路实现简单，实验现象丰富，便于在教学中演示．

2 混沌控制电路的设计

本文采用如下混沌系统［8］：

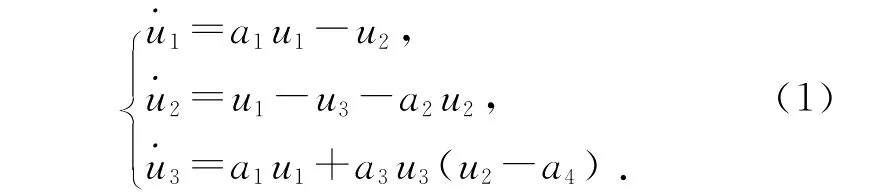
当a1＝0．3，a2＝0．02，a3＝4．0，a4＝1．0时，系统有1个大于零的Lyapunov指数存在，此时系统是混沌的．

根据式（1）设计的混沌电路见图1．集成运放分别构成积分、加法和比例运算电路，乘法器实现非线性函数的功能，为满足式（1）中各参量的要求，选取R＝10 kΩ，R1＝33 kΩ，R2＝500 kΩ，R3＝0．25 kΩ，V1＝1 V，C＝22 nF．

由示波器观测到实验结果如图2所示，图2（a）反映系统运动轨迹在其相空间投影到u1（横轴）～u2（纵轴）平面上所呈现的缠绕和折叠的几何图形，即混沌吸引子，而图2（b）则反映系统运动随时间变化的不规则性．

实现控制的电路如图3所示，其中A6和A7构成2级级联的低通滤波器，A8构成减法器．选取混沌电路中的变量u1作为滤波器的输入信号，经过低通滤波后从运放A7输出，得到的输出信号uO7与u1相减，通过电阻Rw回送给图1电路中的N点，即将控制信号送入式（1）中的第一个方程的右端，此时控制信号可描述为

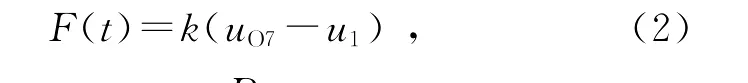
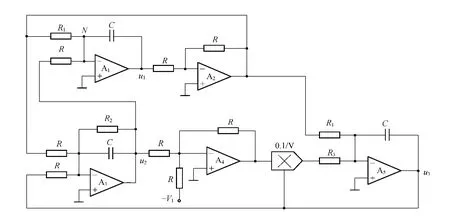
图1 混沌电路

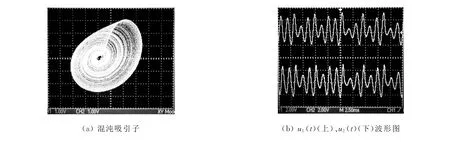
图2 混沌电路的实验结果

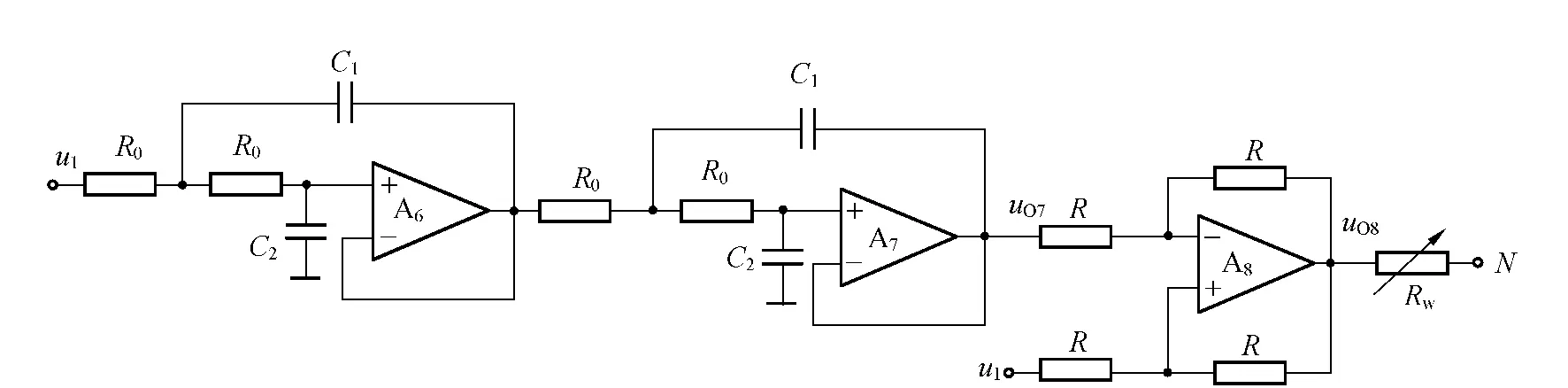
图3 控制电路

3 实验控制的结果

实验中，调节电阻Rw由大到小变化，即相当于k由小到大变化，可以观察到被控混沌电路逐渐由混沌态变为3周期（3P）窗口、4周期（4P）、2周期（2P）、1周期（1P）等倍周期现象．图4（a）～（d）分别为当Rw＝40．2，23．5，20．0，15．5 kΩ时被控电路的实验结果，显然电路分别被控到3P，4P，2P，1P．

图5（a）和图5（b）分别为电路被控制到3P和4P时的时域图，进一步验证电路被控制到周期的结果．

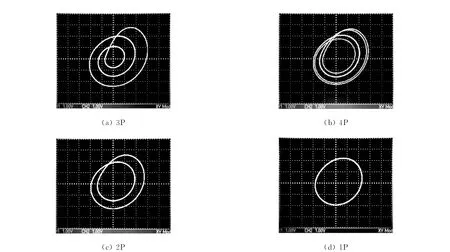
图4 电路被控制到周期的相图（横轴为u1，纵轴为u2）

4 结束语

以三维自治混沌系统为例研究了利用低通滤波器实现混沌控制的方法，适当调节电路元件参量，可以有效地将混沌电路控制到不同的周期态．本文提出的控制方法进一步拓宽了低通滤波器的应用范围．该方法不仅可以控制自治混沌系统，还可以用于控制更高维的超混沌系统．

［1］ Pyragas K．Predictable chaos in slightly perturbed unpredictable chaotic systems ［J］．Phys．Letts．A，1993，181（3）：203－210．

［2］ Ahlborn A，Parlitz U．Chaos control using notch filter feedback［J］．Phys．Rev．Lett．，2006，96：4102－4105．

［3］ Pyragas V，Pyragas K．Delayed feedback control of the Lorenz system：An analytical treatment at a subcritical Hopf bifurcation ［J］．Phys．Rev．E，2006，73（3）：036215－10．

［4］ 李蓉，原如领，汪华英，等．以科研带教学建设“非线性系统实验”课程［J］．物理实验，2002，22（2）：26－28．

［5］ 孙萍，熊俊，曹慧贤，等．扭摆振动实验［J］．物理实验，2006，26（12）：3－7．

［6］ 蒋达娅，王世红，肖井华．混沌专题系列研究型实验介绍［J］．物理实验，2007，27（1）：17－19．

［7］ 路峻岭，王延吉，王长江，等．滚球混沌运动演示实验［J］．物理实验，2007，27（12）：35－38．

［8］ 赵灵冬，陈菊芳，彭建华．变量延迟反馈法控制连续混沌系统的仿真实验［J］．东北师大学报，2004，36（3）：36－41．